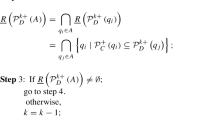Abstract
Aiming at the situation that fuzzy condition attribute values in multi-scale decision table have dominance relations and the decision attribute values are fuzzy, we establish dominance-based fuzzy rough set model (DFRS) in multi-scale decision table (MSDT). In order to investigate the knowledge acquisition efficiency of DFRS in MSDT, we give the optimal scale selection and reduction method to obtain all the optimal scales and all the optimal scale reducts. Besides, we also propose a simple algorithm to obtain an optimal scale reduct. Finally, we verify the effectiveness and practicability of our method through an example of information system security audit risk judgment and a comparative experiment. Experimental results show that our method has obviously improved the knowledge acquisition efficiency compared with the traditional dominance-based fuzzy rough set and effectively integrates the optimal scale selection of the multi-scale decision table with attribute reduction.








Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Pawlak Z (1982) Rough sets. Int J Inf Sci 11:341–356
Morsi NN, Yakout MM (1998) Axiomatics for fuzzy rough sets. Fuzzy Sets Syst 100:327–342
Zhang X, Mei CL, Chen DG, Yang YY (2018) A fuzzy rough set-based feature selection method using representative instances. Knowl-Based Syst 151:216–229
Wang CZ, Huang Y, Shao MW, Fan XD (2019) Fuzzy rough set-based attribute reduction using distance measures. Knowl-Based Syst 164:205–212
Ye J, Zhan JM, Ding WP, Fujita H (2021) A novel fuzzy rough set model with fuzzy neighborhood operators. Inf Sci 544:266–297
Ye J, Zhan JM, Xu ZS (2021) A novel multi-attribute decision-making method based on fuzzy rough sets. Comput Ind Eng. https://doi.org/10.1016/j.cie.2021.107136
An S, Hu QH, Wang CZ (2021) Probability granular distance-based fuzzy rough set model. Appl Soft Comput. https://doi.org/10.1016/j.asoc.2020.107064
Greco S, Matarazzo B, Slowinski R (1999) Rough approximation of a preference relation by dominance relations. Eur J Oper Res 117:63–83
Pan W, She K, Wei PY (2017) Multi-granulation fuzzy preference relation rough set for ordinal decision system. Fuzzy Sets Syst 312:87–108
Du WS, Hu BQ (2017) Dominance-based rough fuzzy set approach and its application to rule induction. Eur J Oper Res 261:690–703
Palangetić M, Cornelis C, Greco S, Słowiński R (2021) Fuzzy extensions of the dominance-based rough set approach. Int J Approximate Reasoning 129:1–19
Sang BB, Chen HM, Yang L, Li TR, Xu WH, Luo C (2021) Feature selection for dynamic interval-valued ordered data based on fuzzy dominance neighborhood rough set. Knowl-Based Syst. https://doi.org/10.1016/j.knosys.2021.107223
Dai JH, Yan YJ, Li ZW, Liao BS (2018) Dominance-based fuzzy rough set approach for incomplete interval-valued data. J Intell Fuzzy Syst 34:423–436
Wang WJ, Zhan JM, Mi JS (2022) A three-way decision approach with probabilistic dominance relations under intuitionistic fuzzy information. Inf Sci 582:114–145
Wei L, Wang YM (2021) A probabilistic interval-valued hesitant fuzzy gained and lost dominance sc-ore method based on regret theory. Comput Ind Eng. https://doi.org/10.1016/j.cie.2021.107532
Yao TL, Wang WL, Miao R, Hu QW, Dong J, Yan XF (2022) Warhead power assessment based on double hierarchy hesitant fuzzy linguistic term sets theory and gained and lost dominance score method. Chin J Aeronaut 35:362–375
Liao ZQ, Liao HC, Tang M, Al-Barakati A, Llopis-Albert C (2020) A Choquet integral-based hesitant fuzzy gained and lost dominance score method for multi-criteria group decision making considering the risk preferences of experts: case study of higher business education evaluation. Info Fusion 62:121–133
Das SS, Islam MM, Arafat NA (2019) Evolutionary algorithm using adaptive fuzzy dominance and reference point for many-objective optimization. Swarm Evol Comput 44:1092–1107
Wu WZ, Leung Y (2011) Theory and applications of granular labelled partitions in multi-scale decision tables. Inf Sci 181:3878–3897
Wu WZ, Leung Y (2013) Optimal scale selection for multi-scale decision tables. Int J Approx Reason 54:1107–1129
Li F, Hu BQ (2017) A new approach of optimal scale selection to multi-scale decision tables. Inf Sci 381:193–208
Li F, Hu BQ, Wang J (2017) Stepwise optimal scale selection for multi-scale decision tables via attribute significance. Knowl-Based Syst 129:4–16
Hao C, Li JH, Fan M, Liu WQ, Tsang ECC (2017) Optimal scale selection in dynamic multi-scale decision tables based on sequential three-way decisions. Inf Sci 415–416:213–232
She YH, Li JH, Yang HL (2015) A local approach to rule induction in multi-scale decision tables. Knowl-Based Syst 89:398–410
Wan Q, Li JH, Wei L, Qian T (2020) Optimal granule level selection: A granule description accuracy viewpoint. Int J Approx Reason 116:85–105
Deng J, Zhan JM, Wu WZ (2021) A three-way decision methodology to multi-attribute decision-making in multi-scale decision information systems. Inf Sci 568:175–198
Zhan JM, Zhang K, Wu WZ (2021) An investigation on Wu-Leung multi-scale information systems and multi-expert group decision-making. Expert Syst Appl. https://doi.org/10.1016/j.eswa.2020.114542
Li WK, Li JJ, Huang JX, Dai WZ, Zhang XP (2021) A new rough set model based on multi-scale covering. Int J Mach Learn Cybern 12:243–256
Huang B, Li HX, Feng GF, Zhou XZ (2019) Dominance-based rough sets in multi-scale intuitionistic fuzzy decision tables. Appl Math Comput 348:487–512
Huang B, Wu WZ, Yan JJ, Li HX, Zhou XZ (2020) Inclusion measure-based multi-granulation decision-theoretic rough sets in multi-scale intuitionistic fuzzy information tables. Inf Sci 507:421–448
Sun BZ, Zhou XM, Lin NN (2020) Diversified binary relation-based fuzzy multigranulation rough set over two universes and application to multiple attribute group decision making. Inf Fusion 55:91–104
Zhang QH, Cheng YL, Zhao F, Wang GY, Xia SY (2021) Optimal scale combination selection integrating three-way decision with Hasse diagram. IEEE Trans Neural Netw Learn Syst. https://doi.org/10.1109/TNNLS.2021.3054063
Cheng YL, Zhang QH, Wang GY (2021) Optimal scale combination selection for multi-scale decision tables based on three-way decision. Int J Mach Learn Cybern 12:281–301
Li WK, Huang JX, Li JJ, Dai WZ (2021) Matrix representation of optimal scale for generalized multi-scale decision table. J Ambient Intell Humaniz Comput 12:8549–8559
Zhou P, Hu XG, Li PP, Wu XD (2019) Online streaming feature selection using adapted Neighborhood Rough Set. Inf Sci 481:258–279
Xia SY, Wang C, Wang GY, Ding WP, Gao XB, Yu JH, Zhai YJ, Chen ZZ (2022) GBRS: An unified model of Pawlak rough set and neighborhood rough set. arXiv preprint arXiv:2201.03349
Xia SY, Zhang H, Li WH, Wang GY, Giem E, Chen ZZ (2020) GBNRS: a novel rough set algorithm for fast adaptive attribute reduction in classification. IEEE Trans Knowl Data Eng 34:1231–1242
Hadrani A, Guennoun K, Saadane R, Wahbi M (2020) Fuzzy rough sets: Survey and proposal of an enhanced knowledge representation model based on automatic noisy sample detection. Cogn Syst Res 64:37–56
Du WS, Hu BQ (2016) Dominance-based rough set approach to incomplete ordered information systems. Inf Sci 346–347:106–129
Zhai YJ, Zhang H (2012) Dominance-based multigranulation rough fuzzy sets and acquisition of decision rules. J Jiangsu Univ 33:310–315
Huang B, Zhuang YL, Li HX, Wei DK (2013) A dominance intuitionistic fuzzy-rough set approach and its applications. Appl Math Model 37:7128–7141
Liu Y, Xiong XX, Liu J (2018) Decision making on dominant intuitionistic fuzzy rough set and its application. J Syst Manag 27:538–545+558
Acknowledgements
This work was supported by Project supported by the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (Grant No. 20KJA520006) and the Postgraduate Research and Practice Innovation Project in Jiangsu Province (Grant No. KYCX20_1681).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Yang, X., Huang, B. Dominance-based fuzzy rough sets in multi-scale decision tables. Int. J. Mach. Learn. & Cyber. 13, 3849–3866 (2022). https://doi.org/10.1007/s13042-022-01629-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13042-022-01629-0