Skip to main content

Advertisement

Springer Nature Link
Log in

Effective weight function in graphs-based discriminant neighborhood embedding

  • Original Article
  • Published:
International Journal of Machine Learning and Cybernetics Aims and scope Submit manuscript

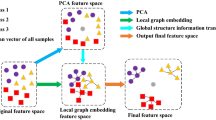
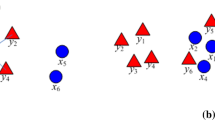
Abstract

Graph embedding-based discriminative dimensionality reduction has attracted much more attention over the past few decades. In constructing adjacent graphs in graph embedding, the weight functions are crucial. The weight function is always found experimentally in practice. So far, there is no any theorem to guide the selection of weight functions. In this study, from the view point of hypothesis-margin, a theoretical framework has been presented to answer the problem above, which can guarantee the fact that the selected weight functions based on the proposed theorem can achieve large hypothesis-margin between near neighbors, improving the classification performance. Then, based on the proposed framework, we design a series of more discriminant weight functions. Sequentially, by constructing double adjacency graphs, we propose a more effective weighted double adjacency graphs-based discriminant neighborhood embedding (WDAG-DNE). Experimental results illustrate that the proposed theorem and WDAG-DNE are more effective.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4.
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Notes

  1. http://www.cad.zju.edu.cn/home/dengcai/Data/FaceData.html.

  2. https://www.sheffield.ac.uk/eee/research/iel/research/face.

References

  1. Shen XJ, Liu SX, Bao BK (2020) A generalized least-squares approach regularized with graph embedding for dimensionality reduction. Pattern Recognit 98:107023

    Article  Google Scholar 

  2. He XF, Yan SC, Hu YX, Niyogi P, Zhang HJ (2005) Face recognition using Laplacianfaces. Pattern Anal Mach Intell 27:328–340

    Article  Google Scholar 

  3. Turk M, Pentland A (1991) Eigenfaces for recognition. J Neurosci 3(1):71–86

    Google Scholar 

  4. P.N. Belhumeur, J.P. Hespanha, D. Kriegman, Eigenfaces vs. Fisherfaces: Recognition using class specific linear projection. IEEE Trans. Pattern Anal. Mach.Intell. 19 (7) (1997) 711–720.

  5. Belkin M, Niyogi P (2003) Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput 15:1373–1396

    Article  MATH  Google Scholar 

  6. X. He, S. Yan, Y. Hu, et al. Face recognition using laplacianfaces. IEEE Transactions on Pattern Analysis & Machine Intelligence (2005) 328–340.

  7. Cai H, Zheng V, Chang K (2017) A comprehensive survey of graph embedding: problems, techniques and applications. IEEE T Knowl DATA En 30(9):1616–1637

    Article  Google Scholar 

  8. Goyal P, Ferrara E (2018) Graph embedding techniques, applications, and performance: a survey. Knowl-Based Syst 151:78–94

    Article  Google Scholar 

  9. Roweis ST, Saul LK (2000) Nonlinear dimensionality reduction by locally linear embedding. Science 290:2323–2326

    Article  Google Scholar 

  10. M. Balasubramanian, E. Schwartz, J. Tenenbaum, V.d. Silva, J. C. Langford.The isomap algorithm and topological stability. Science 295 (2002)7a-7.

  11. H.C. Qu, L. Li, Z.N. Li, et al. Supervised discriminant isomap with maximum margin graph regularization for dimensionality reduction. Expert Syst. Appl. 180(15)(2021)115055.

  12. He X, Yan S, Hu Y et al (2005) Face recognition using Laplacian faces. IEEE T Pattern Anal 27(3):328–340

    Article  Google Scholar 

  13. D. Lu, C. Ding, J. Xu, S. Wang, Hierarchical discriminant analysis. Sensors, 18(1)(2018) 279.

  14. Yang X, Liu G, Yu Q, Wang R (2018) Stable and orthogonal local discriminant embedding using trace ratio criterion for dimensionality reduction. Multimed Tools Appl 77(3):3071–3081

    Article  Google Scholar 

  15. X.F. He, D. Cai, S.C. Yan, H.J. Zhang, Neighborhood preserving embedding. In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV’05), Beijing, China, 17–21 October 2005; Volume 1, pp. 1208–1213.

  16. Yan S, Xu D, Zhang B et al (2007) Graph embedding and extensions: A general framework for dimensionality reduction. IEEE Trans Pattern Anal Mach Intell 29(1):40–51

    Article  Google Scholar 

  17. H.T. Chen, H.W. Chang, T.L. Liu, Local discriminant embedding and its variants, in: Proceedings of International Conference on Computer Vision and Pattern Recognition, 2005.

  18. Zhang W, Xue XY, Lu H, Guo YF (2006) Discriminant neighborhood embedding for classification. Pattern Recognit 39:2240–2243

    Article  MATH  Google Scholar 

  19. Ding CT, Zhang L (2015) Double adjacency graphs-based discriminant neighborhood embedding. Pattern Recogn 48:1734–1742

    Article  MATH  Google Scholar 

  20. You Q, Zheng N, Du S, Wu Y (2007) Neighborhood discriminant projection for face recognition. Pattern Recogn Lett. https://doi.org/10.1016/j.patrec.2007.01.011

    Article  Google Scholar 

  21. M. Wan, Z. Lou, Z. Jin, Margin Maximum Embedding Discriminant (MMED) for Feature Extraction and Classification. IEEE Chinese Conference on Pattern Recognition, Nanjing, China, 2009, pp. 1–5

  22. Sugiyama M (2007) Dimensionality reduction of multimodal labeled data by local fisher discriminant analysis. J Mach Learning Res 8:1027–1061

    MATH  Google Scholar 

  23. D. Cai, X. He, K. Zhou, J. Han, and H. Bao, Locality sensitive discriminant analysis, in Proc. Joint Conf. Artificial Intell.(IJCAI) (2007) 1713–1726.

  24. C.T. Ding, Q.B. Sun, LBDAG-DNE: Locality Balanced Subspace Learning for Image Recognition. Collaborate Computing: Networking, Applications and Worksharing, 2017, pp. 199–210.

  25. Gou JP, Yi Z (2013) Locality-Based Discriminant Neighborhood Embedding. Comput J 9:1063–1082

    Article  Google Scholar 

  26. J.P. Gou, Y.Z. Zhan, M. Wan, et al, Maximum neighborhood margin discriminant projection for classification. The Scientific World Journal. (2014)16, http://dx.doi.org/https://doi.org/10.1155/2014/186749.

  27. Huang P, Chen C, Tang Z, Yang Z (2014) Feature extraction using local structure preserving discriminant analysis. Neurocomputing 140:104–113

    Article  Google Scholar 

  28. Gou J, Yang Y, Yi Z, Lv J, Zhan Y (2019) Discriminative globality and locality preserving graph embedding for dimensionality reduction. Expert Syst Appl 144:113079

    Article  Google Scholar 

  29. S. Wang, C. Ding, C. H. Hsu, F. Yang, Dimensionality reduction via preserving local information. Future Gener Comp. Sys. (2018)S0167739X17319696.

  30. Hu HS, Feng DZ, Chen QY (2020) A novel dimensionality reduction method: Similarity order preserving discriminant analysis. Signal Process 182:107933

    Article  Google Scholar 

  31. Gao Y, Zhang Y, Pan J et al (2021) Discriminant Analysis based on Reliability of Local Neighborhood. Expert Syst Appl 175:114790

    Article  Google Scholar 

  32. Liu Z, Shi K, Zhang K et al (2020) Discriminative sparse embedding based on adaptive graph for dimension reduction. Eng Appl Artif Intel 94:103758

    Article  Google Scholar 

  33. Wong WK, Zhao HT (2012) Supervised optimal locality preserving projection. Pattern Recogn 45(1):186–197

    Article  MATH  Google Scholar 

  34. Duda R, Hart P, Stork D (2000) Pattern Classification, 2nd edn. John Wiley & Sons, USA

    MATH  Google Scholar 

  35. R. G. Bachrach, A, Navot,N. Tishby, Margin based feature selection-Theory and algorithms. In: Proc. of the 21st Int'l Conf. on Machine Learning. Banff: ACM Press, 2004, pp. 43–50

  36. K. Crammer, R. Gilad-Bachrach, A. Navot, N. Tishby. Margin analysis of the lvq algorithm. In: Proceedings of 17th Conference on Neural Information Processing Systems, 2002.

  37. P.J. Phillips, The facial recognition technology (FERET) database <http://www.itl.nist.gov/iad/humanid /feret/feret_master.html> 2004.

  38. A.M.Martinez,R.Benavente,The AR face database.<http://cobweb.ec-n.purdue.edu/aleix/ aleix_face_DB.html>.

  39. Yang J, Zhang D, Yang J, Niu B (2007) Globally maximizing, locally minimizing: unsupervised discriminant projection with applications to face and palm biometrics. IEEE T Patt Anal Mach Intell 29(4):650–664

    Article  Google Scholar 

  40. M. Alshawabkeh, J. A. Aslam, J. G. Dy, D. Kaeli, Feature Weighting and Selection Using Hypothesis Margin of Boosting. IEEE International Conference on Data Mining, IEEE, (2013).

  41. Zhang C, Wang G, Yu B, Xie Y, Pan K (2020) Proximity-aware heterogeneous information network embedding. Knowl-Based Syst 193:105468

    Article  Google Scholar 

  42. Ali Z, Qi G, Muhammad K, Ali B, Abro W (2020) Paper recommendation based on heterogeneous network embedding. Knowl-Based Syst 210:106438

    Article  Google Scholar 

  43. Yu B, Lu B, Zhang C, Li C, Pan K (2020) Node proximity preserved dynamic network embedding via matrix perturbation. Knowl-Based Syst 196:105822

    Article  Google Scholar 

  44. Lai Z, Mo D, Wen J, Shen L, Wong WK (2019) Generalized robust regression for jointly sparse subspace learning. IEEE Trans Circ Syst Vid 29(3):756–772

    Article  Google Scholar 

  45. Lu JL, Lai ZH, Wang HL et al (2022) Generalized Embedding Regression: A Framework for Supervised Feature Extraction. IEEE Trans Neural Networks Learn Syst 33(1):185–199

    Article  Google Scholar 

Download references

Acknowledgements

This work is supported in part by Open fund project of national rare earth permanent magnet motor engineering technology research center (Grant No. 21AZ12), in part by the Henan Key Laboratory of Smart Lighting.

Author information

Authors and Affiliations

  1. School of Electronic Information Engineering, Shanghai Dian Ji University, Shanghai, 201306, China

    Guodong Zhao

  2. School of Art and Design, Shanghai Dian Ji University, Shanghai, 201306, China

    Zhiyong Zhou

  3. School of Biomedical Engineering, Shanghai Jiao Tong University, Shanghai, 200240, China

    Zhiyong Zhou

  4. College of Information Engineering, Huanghuai University, Henan, 463000, China

    Li Sun & Junming Zhang

  5. Henan Key Laboratory of Smart Lighting, Henan, 463000, China

    Guodong Zhao, Li Sun & Junming Zhang

Authors
  1. Guodong Zhao
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Zhiyong Zhou
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Li Sun
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Junming Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Guodong Zhao.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhao, G., Zhou, Z., Sun, L. et al. Effective weight function in graphs-based discriminant neighborhood embedding. Int. J. Mach. Learn. & Cyber. 14, 347–360 (2023). https://doi.org/10.1007/s13042-022-01643-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13042-022-01643-2

Keywords