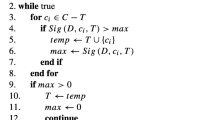Abstract
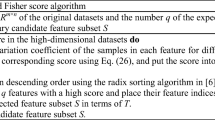
The optimal global feature subset cannot be found easily due to the high cost, and most swarm intelligence optimization-based feature selection methods are inefficient in handling high-dimensional data. In this study, a two-stage feature selection model based on fuzzy neighborhood rough sets (FNRS) and binary whale optimization algorithm (BWOA) is developed. First, to denote the fuzziness of samples for mixed data with symbolic and numerical features, fuzzy neighborhood similarity is presented to study the similarity matrix and fuzzy membership degree, and the lower and upper approximations can be developed to present new FNRS model. Fuzzy neighborhood-based uncertainty measures such as dependence degree, knowledge granularity, and entropy measures are studied. From the viewpoints of algebra and information, fuzzy knowledge granularity conditional entropy is presented to form a preselected feature reduction set in the first stage. Second, the cosine curve change is added to develop a new control factor, which slows down the convergence rate of BWOA in the early iteration to fully explore the global, and accelerates the convergence rate in the late iteration. Integrating dependence degree with fuzzy knowledge granularity conditional entropy, a new fitness function is designed for selecting an optimal feature subset in this second stage. Two strategies are fused to avoid BWOA falling into the local optimum: the population partition strategy with the adaptive neighborhood search radius to divide the whale population and the local interference strategy of the elite subgroup to adjust the whale position update. Finally, a two-stage feature selection algorithm is designed, where the Fisher score algorithm is employed to preliminarily delete those redundancy features of high-dimensional datasets. Experiments on six UCI datasets and five gene expression datasets show that our algorithm is valid compared to other related algorithms.







Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Zhang X, Yao Y (2022) Tri-level attribute reduction in rough set theory. Expert Syst Appl 190:116187
Ding W, Pedrycz W, Triguero I, Cao Z, Lin C (2021) Multigranulation supertrust model for attribute reduction. IEEE Trans Fuzzy Syst 29(6):1395–1408
Qian W, Dong P, Wang Y, Dai S, Huang J (2022) Local rough set-based feature selection for label distribution learning with incomplete labels. Int J Mach Learn Cybern 13:2345–2364
Sun L, Zhang X, Qian Y, Xu J, Zhang S (2019) Feature selection using neighborhood entropy-based uncertainty measures for gene expression data classification. Inf Sci 502:18–41
Sun L, Li M, Ding W, Zhang E, Mu X, Xu J (2022) AFNFS: Adaptive fuzzy neighborhood-based feature selection with adaptive synthetic over-sampling for imbalanced data. Inf Sci 612:724–744
Xu W, Yuan K, Li W (2022) Dynamic updating approximations of local generalized multigranulation neighborhood rough set. Appl Intell 52(8):9148–9173
Sun L, Huang M, Xu J (2022) Weak label feature selection method based on neighborhood rough sets and Relief. Chin Comput Sci 49(4):152–160
Zhang C, Ding J, Zhan J, Li D (2022) Incomplete three-way multi-attribute group decision making based on adjustable multigranulation Pythagorean fuzzy probabilistic rough sets. Int J Approx Reason 147:40–59
Zhang C, Li D, Liang J (2020) Multi-granularity three-way decisions with adjustable hesitant fuzzy linguistic multigranulation decision-theoretic rough sets over two universes. Inf Sci 507:665–683
Sun L, Wang X, Ding W, Xu J (2022) TSFNFR: Two-stage fuzzy neighborhood-based feature reduction with binary whale optimization algorithm for imbalanced data classification. Knowl Based Syst 256:109849
Sun L, Zhang J, Ding W, Xu J (2022) Feature reduction for imbalanced data classification using similarity-based feature clustering with adaptive weighted k-nearest neighbors. Inf Sci 593:591–613
Sun L, Wang L, Ding W, Qian Y, Xu J (2021) Feature selection using fuzzy neighborhood entropy-based uncertainty measures for fuzzy neighborhood multigranulation rough sets. IEEE Trans Fuzzy Syst 29(1):19–33
Sun L, Wang W, Xu J, Zhang S (2019) Improved LLE and neighborhood rough sets-based gene selection using Lebesgue measure for cancer classification on gene expression data. J Intell Fuzzy Syst 37(4):5731–5742
Zhang X, Jiang J (2022) Measurement, modeling, reduction of decision-theoretic multigranulation fuzzy rough sets based on three-way decisions. Inf Sci 607:1550–1582
Sun L, Xu J, Tian Y (2012) Feature selection using rough entropy-based uncertainty measures in incomplete decision systems. Knowl Based Syst 36:206–216
Xu W, Yuan K, Li W, Ding W (2022) An emerging fuzzy feature selection method using composite entropy-based uncertainty measure and data distribution. IEEE Trans Emerg Top Comput Intell. https://doi.org/10.1109/TETCI.2022.3171784
Xu W, Li W (2016) Granular computing approach to two-way learning based on formal concept analysis in fuzzy datasets. IEEE Trans Cybern 46(2):366–379
Li W, Zhou H, Xu W, Wang X, Pedrycz W (2022) Interval dominance-based feature selection for interval-valued ordered data. IEEE Trans Neural Netw Learn Syst. https://doi.org/10.1109/TNNLS.2022.3184120
Sun L, Yin T, Ding W, Qian Y, Xu J (2022) Feature selection with missing labels using multilabel fuzzy neighborhood rough sets and maximum relevance minimum redundancy. IEEE Trans Fuzzy Syst 30(5):1197–1211
Sun L, Wang L, Ding W, Qian Y, Xu J (2020) Neighborhood multi-granulation rough sets-based attribute reduction using Lebesgue and entropy measures in incomplete neighborhood decision systems. Knowl Based Syst 192:105373
Sun L, Wang L, Qian Y, Xu J, Zhang S (2019) Feature selection using Lebesgue and entropy measures for incomplete neighborhood decision systems. Knowl Based Syst 186:104942
Shu W, Qian W, Xie Y (2020) Incremental feature selection for dynamic hybrid data using neighborhood rough set. Knowl Based Syst 194:105516
Chen Y, Chen Y (2021) Feature subset selection based on variable precision neighborhood rough sets. Int J Comput Intell Syst 14(1):572–581
Tan A, Wu W, Qian Y, Liang J, Chen J, Li J (2019) Intuitionistic fuzzy rough set-based granular structures and attribute subset selection. IEEE Trans Fuzzy Syst 27(3):527–539
Zeng K, She K, Niu X (2013) Multi-granulation entropy and its applications. Entropy 15(6):2288–2302
Chen D, Yang Y (2014) Attribute reduction for heterogeneous data based on the combination of classical and fuzzy rough set models. IEEE Trans Fuzzy Syst 22(5):1325–1334
Wang C, Shao M, He Q, Qian Y, Qi Y (2016) Feature subset selection based on fuzzy neighborhood rough sets. Knowl Based Syst 111:173–179
Zhang X, Fan Y, Yang J (2021) Feature selection based on fuzzy-neighborhood relative decision entropy. Pattern Recogn Lett 146:100–107
Xu J, Wang Y, Mu H, Huang F (2019) Feature genes selection based on fuzzy neighborhood conditional entropy. J Intell Fuzzy Syst 36(1):117–126
Sun L, Si S, Zhao J, Xu J, Lin Y, Lv Z (2022) Feature selection using binary monarch butterfly optimization. Appl Intell. https://doi.org/10.1007/s10489-022-03554-9
Fan X, Chen H (2020) Stepwise optimized feature selection algorithm based on discernibility matrix and mRMR. Chin Comput Sci 47(1):87–95
Mirjalili S, Lewis A (2016) The whale optimization algorithm. Adv Eng Softw 95:51–67
Tian M, Liang X, Fu X, Sun Y, Li Z (2021) Multi-subgroup particle swarm optimization with game probability selection. Chin Comput Sci 48(10):67–76
Sun L, Kong X, Xu J, Xue Z, Zhai R, Zhang S (2019) A hybrid gene selection method based on ReliefF and Ant Colony Optimization algorithm for tumor classification. Sci Rep 9:8978
Sanjoy C, Apu K, Ratul C, Moumita S (2021) An enhanced whale optimization algorithm for large scale optimization problems. Knowl Based Syst 233:107543
Zheng Y, Li Y, Wang G, Chen Y, Xu Q, Fan J, Cui X (2019) A novel hybrid algorithm for feature selection based on whale optimization algorithm. IEEE Access 7:14908–14923
Moorthy U, Gandhi U (2021) A novel optimal feature selection technique for medical data classification using ANOVA based whale optimization. J Ambient Intell Humaniz Comput 12:3527–3538
Tawhid M, Ibrahim A (2020) Feature selection based on rough set approach, wrapper approach, and binary whale optimization algorithm. Int J Mach Learn Cybern 11(3):573–602
Wang S, Chen H (2020) Feature selection method based on rough sets and improved whale optimization algorithm. Chin Comput Sci 47(2):44–50
Sun L, Wang T, Ding W, Xu J, Tan A (2022) Two-stage-neighborhood-based multilabel classification for incomplete data with missing labels. Int J Intell Syst 37:6773–6810
Sun L, Zhang J, Ding W, Xu J (2022) Mixed measure-based feature selection using the Fisher score and neighborhood rough sets. Appl Intell. https://doi.org/10.1007/s10489-021-03142-3
Fang B, Chen H, Wang S (2019) Feature selection algorithm based on rough sets and fruit fly optimization. Chin Comput Sci 46(7):157–164
Sun L, Qin X, Ding W, Xu J (2022) Nearest neighbors-based adaptive density peaks clustering with optimized allocation strategy. Neurocomputing 473:159–181
Sun L, Qin X, Ding W, Xu J, Zhang S (2021) Density peaks clustering based on k-nearest neighbors and self-recommendation. Int J Mach Learn Cybern 12(7):1913–1938
Sun L, Zhang X, Qian Y, Xu J, Zhang S, Tian Y (2019) Joint neighborhood entropy-based gene selection method with fisher score for tumor classification. Appl Intell 49(4):1245–1259
Chen Y, Zhang Z, Zheng J, Ma Y, Xue Y (2017) Gene selection for tumor classification using neighborhood rough sets and entropy measures. J Biomed Inform 67:59–68
Xu F, Miao D, Wei L (2009) Fuzzy-rough attribute reduction via mutual information with an application to cancer classification. Comput Math Appl 57(6):1010–1017
Faramarzi A, Heidarinejad M, Stephens B, Mirjalili S (2020) Equilibrium optimizer: a novel optimization algorithm. Knowl Based Syst 191:105190
Faramaizi A, Heidarinejad M, Mirjalili S, Gandomi A (2020) Marine predators algorithm: a nature-inspired metaheuristic. Expert Syst Appl 152:113377
Bozorgi S, Yazdani S (2019) IWOA: an improved whale optimization algorithm for optimization problems. J Comput Des Eng 6(3):243–259
Fan Q, Chen Z, Zhang W, Fang X (2020) ESSAWOA: enhanced whale optimization algorithm integrated with Salp Swarm Algorithm for global optimization. Eng Comput. https://doi.org/10.1007/s00366-020-01189-3
Chakraborty S, Saha A, Sharma S, Chakraborty R, Debnath S (2021) A hybrid whale optimization algorithm for global optimization. J Ambient Intell Humaniz Comput. https://doi.org/10.1007/s12652-021-03304-8
Hu Q, Yu D, Xie Z (2006) Information-preserving hybrid data reduction based on fuzzy-rough techniques. Pattern Recogn Lett 27(5):414–423
Sun L, Wang T, Ding W, Xu J, Lin Y (2021) Feature selection using Fisher score and multilabel neighborhood rough sets for multilabel classification. Inf Sci 578:887–912
Xu J, Shen K, Sun L (2022) Multi-label feature selection based on fuzzy neighborhood rough sets. Complex Intell Syst 8(3):2105–2129
Sun L, Yin T, Ding W, Qian Y, Xu J (2020) Multilabel feature selection using ML-ReliefF and neighborhood mutual information for multilabel neighborhood decision systems. Inf Sci 537:401–424
Acknowledgements
This research was funded by the National Natural Science Foundation of China under Grants 62076089, 61772176, 61976082, 61976120, and 61901160; the Excellent Science and Technology Innovation Team of Henan Normal University under Grant 2021TD05; and the Natural Science Foundation of Jiangsu Province under Grant BK20191445.
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Sun, L., Wang, X., Ding, W. et al. TSFNFS: two-stage-fuzzy-neighborhood feature selection with binary whale optimization algorithm. Int. J. Mach. Learn. & Cyber. 14, 609–631 (2023). https://doi.org/10.1007/s13042-022-01653-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13042-022-01653-0