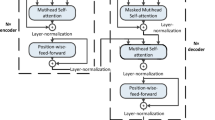
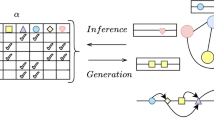
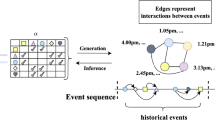
Abstract
Modeling Hawkes process using deep learning is superior to traditional statistical methods in the goodness of fit. However, methods based on RNN or self-attention are deficient in long-time dependence and recursive induction, respectively. Universal Transformer (UT) is an advanced framework to integrate these two requirements simultaneously due to its continuous transformation of self-attention in the depth of the position. In addition, migration of the UT framework involves the problem of effectively matching Hawkes process modeling. Thus, in this paper, an iterative convolutional enhancing self-attention Hawkes process with time relative position encoding (ICAHP-TR) is proposed, which is based on improved UT. First, the embedding maps from dense layers are carried out on sequences of arrival time points and markers to enrich event representation. Second, the deep network composed of UT extracts hidden historical information from event expression with the characteristics of recursion and the global receptive field. Third, two designed mechanics, including the relative positional encoding on the time step and the convolution enhancing perceptual attention are adopted to avoid losing dependencies between relative and adjacent positions in the Hawkes process. Finally, the hidden historical information is mapped by Dense layers as parameters in Hawkes process intensity function, thereby obtaining the likelihood function as the network loss. The experimental results show that the proposed methods demonstrate the effectiveness of synthetic datasets and real-world datasets from the perspective of both the goodness of fit and predictive ability compared with other baseline methods.








Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Data availability
The data that support the findings of this study are openly available in a public repository ifl-tpp at https://github.com/shchur/ifl-tpp.
References
Du N, Dai H, Trivedi R, Upadhyay U, Gomez-Rodriguez M, and Song L (2016) Recurrent marked temporal point processes: Embedding event history to vector. In: Proceedings of ACM SIGKDD International Conference on knowledge discovery and data mining, pp 1555–1564. https://doi.org/10.1145/2939672.2939875
Gao H, Huang T, Liu Y, Yin Y, Li Y (2022) PPO2: location privacy-oriented task offloading to edge computing using reinforcement learning for intelligent autonomous transport systems. IEEE Trans Neural Netw Learn Syst. https://doi.org/10.1109/TITS.2022.316-9421
Dai Z, Zhou H, Dong X (2020) Forecasting stock market volatility: the role of gold and exchange rate. AIMS Math 5(5):5094–5105. https://doi.org/10.3934/math.2020327
Gao H, Qiu B, Duran Barroso RJ, Hussain W, Xu Y, Wang X (2022) TSMAE: a novel anomaly detection approach for internet of things time series data using memory-augmented autoencoder. IEEE Trans Netw Sci Eng. https://doi.org/10.1109/TNSE.2022.3163144
Tang L, Zheng S, Zhou Z (2018) Estimation and test of restricted linear EV model with nonignorable missing covariates. Appl Math-A J Chin Univ 33(3):344–358. https://doi.org/10.1007/s11766-018-3550-8
Zhou Z, Tang L (2019) Testing for parametric component of partially linear models with missing covariates. Stat Pap 60(3):747–760. https://doi.org/10.1007/s00362-016-0848-6
Tan Z, Zheng S (2020) Extremes of a type of locally stationary Gaussian random fields with applications to Shepp statistics. J Theor Probab 33(4):2258–2279. https://doi.org/10.1007/s10959-019-00953-6
Chen Y, Tan Z (2019) Almost sure limit theorem for the order statistics of stationary Gaussian sequences. Filomat 32(9):3355–3364. https://doi.org/10.2298/FIL1809355C
Alan GH (1971) Spectra of some self-exciting and mutually exciting point processes. Biometrika 58:83–90. https://academic.oup.com/biomet/article/58/1/83/224809. Accessed 28 May 2021
Omi T, Ueda N, Aihara K (2019) Fully neural network-based model for general temporal point processes. arXiv preprint arXiv:1905.09690
Shchur O, Biloš M, Günnemann S (2019) Intensity-free learning of temporal point processes. arXiv preprint arXiv:1909.12127
Zhang Q, Lipani A, Kirnap O, and Yilmaz E (2019) Self-attentive Hawkes processes. arXiv preprint arXiv:1907.07561, 2019.
Zuo S, Jiang H, Li Z, Zhao T, Zha H (2020) Transformer Hawkes process. In: Proceedings of the 37th International Conference on machine learning, vol 119, pp 11692–11702
Gao H, Xu K, Cao M, Xiao J, Xu Q, Yin Y (2021) The deep features and attention mechanism-based method to dish healthcare under social IoT systems: an empirical study with a hand-deep local-global net. IEEE Trans Netw Sci Eng 9(1):336–347. https://doi.org/10.1109/TCSS.2021.3102591
Xiao J, Xu H, Gao H, Bian M, Li Y (2021) A weakly supervised semantic segmentation network by aggregating seed cues: the multi-object proposal generation perspective. ACM Trans Multimed Comput Commun Appl 17(1s):1–19. https://doi.org/10.1145/3-419842
Huang C, Liu B, Qian C, Cao J (2021) Stability on positive pseudo almost periodic solutions of HPDCNNs incorporating D operator. Math Comput Simul 190(2021):1150–1163. https://doi.org/10.1016/j.matcom.2021.06.027
Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez AN, Kaiser L, and Polosukhin I (2017) Attention is all you need. In: Proceedings of the 31st lnternational Conference on Neural lnformation Processing Systems, pp 6000–6010
Bengio Y (1994) Learning long-term dependencies with gradient descent difficult. IEEE Trans Neural Netw 5(2):157–166. https://ieeexplore.ieee.org/document/279181. Accessed 3 Apr 2021
Dehghani M, Gouws S, Vinyals O, Uszkoreit J, Kaiser U (2019) Universal transformers. In: Proceedings of the International Conference on learning representations, OpenReview.net. https://openreview.net/forum?id=HyzdRiR9Y7. Accessed 1 Apr 2021
Shaw P, Uszkoreit J, Vaswani A (2018) Self-attention with relative position representations. arXiv preprint arXiv:1803.02155
Su J, Wang Z, Chen M (2020) Orthogonal exponential functions of the planar self-affine measures with four digits. Fractals. https://doi.org/10.1142/S0218348X20500164
Li J, Li P (2018) Inverse elastic scattering for a random source. SIAM J Math Anal 51(6):4570–4603. https://doi.org/10.1137/18M1235119
Mei H, Eisner JM (2017) The neural Hawkes process: a neurally self-modulating multivariate point process. In: Proceedings of the 31st International Conference on Neural Information Processing Systems, pp 6754–6764
Lin Z, Feng M, Santos C, Yu M, Xiang B, Zhou B, Bengio Y (2017) A structured self-attentive sentence embedding. arXiv preprint arXiv:1703.03130
Gao H, Xiao J, Yin Y, Liu T, Shi J (2022) A mutually supervised graph attention network for few-shot segmentation: the perspective of fully utilizing limited samples. IEEE Trans Neural Netw Learn Syst. https://doi.org/10.1109/TNNLS.2022.3155486
Zhang L, Liu J, Song Z, Xin Z (2021) Universal Transformer Hawkes process with adaptive recursive iteration. Eng Appl Artif Intell. https://doi.org/10.1016/j.engappai.2021.104416
Guo R, Li J, Liu H (2018) Initiator: noise-contrastive estimation for marked temporal point process. In Proceedings of the International Joint Conference on artificial intelligence, pp 2191–2197. https://doi.org/10.24963/ijcai.2018/303
Xiao S, Farajtabar M, Ye X, Yan J, Song L, and Zha H (2017) Wasserstein learning of deep generative point process models. In: Proceedings of the 31st International Conference on Neural Information Processing Systems, pp 3247–3257
Xiao S, Xu H, Yan J, Farajtabar M, Yang X, Song L, Zha H (2018) Learning conditional generative models for temporal point processes. In: Proceedings of the 32nd AAAI Conference on artificial intelligence, vol 32(1), pp 6302–6310
Li S, Xiao S, Zhu S, Du N, Xie Y, Song L (2018) Learning temporal point processes via reinforcement learning. In: Proceedings of the 32nd Conference on Neural Information Processing Systems, pp 10781–10791
Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R (2014) Dropout: a simple way to prevent neural networks from overfitting. J Mach Learn Res 15(1):1929–1958
Ba JL, Kiros JR, and Hinton GE (2014). Layer normalization. arXiv preprint arXiv:1607.06450, 2016
Graves A, Wayne G, Danihelka I (2014) Neural turing machines. arXiv preprint arXiv:1410.5401
Liu Z, Zhou Y, Zhang Y (2020) On inexact alternating direction implicit iteration for continuous Sylvester equations. Numer Linear Algebra Appl. https://doi.org/10.1002/nla.2320
Zhou W, Zhang L (2020) A modified Broyden-like quasi-Newton method for nonlinear equations. J Comput Appl Math. https://doi.org/10.1016/j.cam.-2020.112744
Ogata Y (1981) On Lewis’ simulation method for point processes. IEEE Trans Inf Theory IT-27(1):23–31
Kumar S, Zhang X, Leskovec J (2019) Predicting dynamic embedding trajectory in Temporal Interaction Networks. In: Proceedings of the ACM SIGKDD International Conference, pp 1269–1278. https://doi.org/10.1145/3292500.3330895.
Acknowledgements
This work was supported by the Applied Basic Research Programs of Shanxi Province (Grant no. 201901D211105).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Bian, W., Li, C., Hou, H. et al. Iterative convolutional enhancing self-attention Hawkes process with time relative position encoding. Int. J. Mach. Learn. & Cyber. 14, 2529–2544 (2023). https://doi.org/10.1007/s13042-023-01780-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13042-023-01780-2