Unsupervised domain adaptation by incremental learning for concept drifting data streams

Abstract

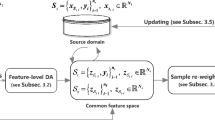
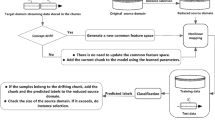
Incremental learning is a learning paradigm in which a model is updated continuously as new data becomes available, and its main challenge is to adapt to non-stationary environments without the time-consuming re-training process. Many efforts have been made on incremental supervised learning. However, providing sufficient labeled data remains a major problem. Recently, domain adaptation methods have gained attention. These methods aim to leverage the knowledge from an auxiliary source domain to boost the performance of the model in the target domain by reducing the domain discrepancy between them. Regarding these issues, in the present paper, a proposed model aims to incrementally learn a new domain characterized by drifts due to a non-stationary environment. It utilizes an unsupervised, fuzzy-based domain adaptation to classify data streams faced with concept drift while accounting for a label-agnostic incremental setting in the target domain. Incremental learning updates occur whenever the entropy-based metric indicates uncertainty, ensuring informative samples are integrated. Also, outdated samples are forgotten during the training stage using the dynamic sample weighting strategy. Through experimentation on forty-five tasks, the superiority of the proposed model in handling dynamic adaptation on non-stationary domains is demonstrated, showcasing improvements in accuracy and computational efficiency.

Appendices

Appendix I

This section contains detailed information for computing the metric $\mathcal{D}$ introduced by [13]. For each fuzzy feature vector ${\overline{A} }_{i}\left({a}_{i1},{a}_{i2},\dots ,{a}_{in}\right)\in F({\mathbb{R}}^{n})$. For each ${\overline{a} }_{ij}\in F({\mathbb{R}})$, its membership function is computed by Eq. (I1).

$${\mu }_{ij}(x|{\overline{a} }_{ij})=\left\{\begin{array}{l}0 \forall x<{a}_{ij}-{\rho }_{i} \\ 1-\frac{{\Vert x-{a}_{ij}\Vert }_{1}}{{\rho }_{i}} \forall {\Vert x-{a}_{ij}\Vert }_{1}\le {\rho }_{i}, \, x\in R \\ 0 \forall x>{a}_{ij}+{\rho }_{i}\end{array}\right.$$

(I1)

where ${a}_{ij}$ indicates the $j$ th feature value of the $i$ th sample and ${\rho }_{i}$ shows the hesitation degree of the $i$ th sample considering a triangular membership function. Utilizing Eq. (I2), ${\mu }_{ij}({\varvec{x}}|{\overline{A} }_{i})$ where ${\varvec{x}}=({x}_{1},{ x}_{2},\dots \text{, }{x}_{n})$ is obtained.

$${\mu }_{ij}\left({\varvec{x}}|{\overline{A} }_{i}\right)=\left\{\begin{array}{l}0 if \exists {x}_{j}, { x}_{j}<{a}_{ij}-{\rho }_{i} \\ 1-\frac{{\Vert {\varvec{x}}-{a}_{ij}\Vert }_{1}}{{n\rho }_{i}} if \forall {x}_{j}, {\Vert x-{a}_{ij}\Vert }_{1}\le {\rho }_{i}, x\in {\mathbb{R}}^{n} \\ 0 if \exists {x}_{j}, { x}_{j}>{a}_{ij}+{\rho }_{i}\end{array}\right.$$

(I2)

To define the fuzzy relation between two heterogeneous domains (source and target), the following metric is defined to measure the distance between the fuzzy vectors.

$$\mathcal{D}\left({\overline{A} }_{i},{\overline{A} }_{j}\right)=\frac{1}{n}\underset{0}{\overset{1}{\int }}sup\left\{{\mathcal{D}}_{\lambda }\left(u,v\right): {\mathcal{D}}_{\lambda }\left(u,v\right)\in\Omega \left(\lambda \right)\right\}d\lambda ; u\in {\overline{A} }_{i}\left(\lambda \right), v\in {\overline{A} }_{j}(\lambda )$$

(I3)

where $\lambda$ is the membership value, ${\mathcal{D}}_{\lambda }\left(u,v\right)$ indicates the distance between points $u$ and $v$ in ${\mathbb{R}}^{n}$ with the given $\lambda$. $\Omega \left(\lambda \right)$ is computed by Eq. (I4).

$$\begin{aligned}\Omega \left(\lambda \right)&=\left\{d(u,{\overline{A} }_{j}(\lambda ))\right\}\cup \left\{d(v,{\overline{A} }_{i}(\lambda ))\right\}\\ d(u,{\overline{A} }_{j}(\lambda ))&=min\left\{d\left(u,v\right), v\in {\overline{A} }_{j}(\lambda )\right\}\\ d(v,{\overline{A} }_{i}(\lambda ))&=min\left\{d\left(v,u\right), u\in {\overline{A} }_{i}(\lambda )\right\}\end{aligned}$$

(I4)

where $d\left(v,u\right)$ is the ${l}_{1}$-norm between two n-dimensional vectors ($u$ and $v$). Note that the supremum operator (sup) in Eq. (I3) indicates the longest distance between the fuzzy vector of one specific domain to the fuzzy set of another domain. Eq. (I3) can be re-written as Eq. (I5).

$$\mathcal{D}\left({\overline{A} }_{i},{\overline{A} }_{j}\right)=\frac{1}{n}\underset{0}{\overset{1}{\int }}d\left({A}_{i},{A}_{j}\right)+\frac{1}{2}\left|d\left(u,{\overline{A} }_{j}\left(\lambda \right)\right)+d(v,{\overline{A} }_{i}(\lambda ))\right|d\lambda$$

(I5)

The above equation is de-fuzzified regarding Eqs. (I1) and (I2) as follows.

$$\begin{aligned}\mathcal{D}\left({\overline{A} }_{i},{\overline{A} }_{j}\right)&=\frac{1}{n}d\left({A}_{i},{A}_{j}\right)+\frac{1}{2}\underset{0}{\overset{1}{\int }}\left|\left(1-\lambda \right){\rho }_{i}-\left(1-\lambda \right){\rho }_{j}\right|d\lambda \\ &=\frac{1}{n}d\left({A}_{i},{A}_{j}\right)+\frac{1}{2}{\Vert {\rho }_{i}-{\rho }_{j}\Vert }_{1}\underset{0}{\overset{1}{\int }}\left(1-\lambda \right)d\lambda \\ & =\frac{1}{n}d\left({A}_{i},{A}_{j}\right)+\frac{1}{4}{\Vert {\rho }_{i}-{\rho }_{j}\Vert }_{1}\end{aligned}$$

(I6)

Eq. (I6) cannot be used directly for computing the fuzzy relation because it does not satisfy two properties of the fuzzy relation, including (1) symmetry, a condition in which $\mathcal{D}\left({\overline{A} }_{i},{\overline{A} }_{j}\right)=\mathcal{D}\left({\overline{A} }_{j},{\overline{A} }_{i}\right)\text{, }\forall {\overline{A} }_{i}\text{, }{\overline{A} }_{j}$ and (2) reflexivity, a condition in which $\mathcal{D}\left({\overline{A} }_{i},{\overline{A} }_{j}\right)=1, \forall {\overline{A} }_{i}$. Thus, the following function is employed.

$${R}_{\mathcal{D}}\left({\overline{A} }_{i},{\overline{A} }_{j}\right)={e}^{-\frac{\mathcal{D}\left({\overline{A} }_{i},{\overline{A} }_{j}\right)}{2{\sigma }^{2}}}$$

(I7)

Appendix II

All the tables of SubSect. 5.3 are presented from here on (See Tables 11, 12, 13, 14, 15 and 16).

Table 11 Average accuracy (%) when sudden drift is inserted

Table 12 Average accuracy (%) when incremental drift is inserted

Table 13 Average accuracy (%) when gradual drift is inserted

Table 14 Computational time (second) when sudden drift is inserted

Table 15 Computational time (second) when incremental drift is inserted

Table 16 Computational time (second) when gradual drift is inserted