Abstract
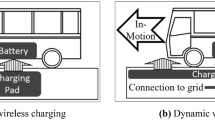
With the emergence of environmental problems, the implementation of electric vehicles in the transport sector presents a solution that meets environmental and economic objectives. For this reason, electric vehicles (EVs) have become increasingly popular as a mainstream transportation solution, opportunities to recharge the vehicle away from home have become a critical issue, and it needs a long waiting time, with a risk of electrocution. One of the solutions to avoid these disadvantages is the wireless charging EVs. For that reason, the main contribution of this work is to propose the strategic location of inductive power transmitters especially when there are several routes between an origin and a destination. Our goal is to find a compromise between the cost of installing the power transmitters and the cost of the battery while maintaining the quality of the vehicle routing. To show the efficiency of our mathematical model and resolution method, we compare our results with the results found in the literature.














Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Pye, S., Li, F.G.N., Price, J., Fais, B.: Achieving net-zero emissions through the reframing of UK national targets in the post-Paris agreement era. Nat. Energy. 2(3), (2017). https://doi.org/10.1038/nenergy.2017.24
Falkner, R.: The Paris agreement and the new logic of international climate politics. Int. Aff. 92(5), 1107–1125 (2016). https://doi.org/10.1111/1468-2346.12708
Mouhrim, N., El Hilali Alaoui, A., Boukachour, J.: Pareto efficient allocation of an in-motion wireless charging infrastructure for electric vehicles in a multipath network. Int. J. Sustain. Transp. 13(6), 419–432 (2019). https://doi.org/10.1080/15568318.2018.1481242
Peterson, S.B., Whitacre, J.F., Apt, J.: The economics of using plug-in hybrid electric vehicle battery packs for grid storage. J. Power Sources. 195(8), 2377–2384 (2010). https://doi.org/10.1016/j.jpowsour.2009.09.070
Ulrich, L.: State of charge. IEEE Spectr. 49(1), 56–59 (2012). https://doi.org/10.1109/MSPEC.2012.6117841
Ko, Y.D., Jang, Y.J.: The optimal system design of the online electric vehicle utilizing wireless power transmission technology. IEEE Trans. Intell. Transp. Syst. 14(3), 1255–1265 (2013). https://doi.org/10.1109/TITS.2013.2259159
Wang, Y.W.: An optimal location choice model for recreation-oriented scooter recharge stations. Transp. Res. Part D Transp. Environ. 12(3), 231–237 (2007). https://doi.org/10.1016/j.trd.2007.02.002
Wang, Y.W.: Locating flow-recharging stations at tourist destinations to serve recreational travelers. Int. J. Sustain. Transp. 5(3), 153–171 (2011). https://doi.org/10.1080/15568311003717199
Wang, Y.W., Lin, C.C.: Locating multiple types of recharging stations for battery-powered electric vehicle transport. Transp. Res. Part E Logist. Transp. Rev. 58, 76–87 (2013). https://doi.org/10.1016/j.tre.2013.07.003
Wang, Y.W.: Locating battery exchange stations to serve tourism transport: a note. Transp. Res. Part D Transp. Environ. 13(3), 193–197 (2008). https://doi.org/10.1016/j.trd.2008.01.003
Yang, J., Sun, H.: Battery swap station location-routing problem with capacitated electric vehicles. Comput. Oper. Res. 55, 217–232 (2015). https://doi.org/10.1016/j.cor.2014.07.003
Hof, J., Schneider, M., Goeke, D.: Solving the battery swap station location-routing problem with capacitated electric vehicles using an AVNS algorithm for vehicle-routing problems with intermediate stops. Transp. Res. Part B Methodol. 97, 102–112 (2017). https://doi.org/10.1016/j.trb.2016.11.009
Zhong, L., Pei, M.: Optimal design for a shared swap charging system considering the electric vehicle battery charging rate. Energies. 13(5), (2020). https://doi.org/10.3390/en13051213
Jang, Y.J., Jeong, S., Lee, M.S.: Initial energy logistics cost analysis for stationary, quasi-dynamic, & dynamicwireless charging public transportation systems. Energies. 9(7), (2016). https://doi.org/10.3390/en9070483
Panchal, C., Stegen, S., Lu, J.: Review of static and dynamic wireless electric vehicle charging system. Eng. Sci. Technol. Int. J. 21(5), 922–937 (2018). https://doi.org/10.1016/j.jestch.2018.06.015
Xiang, L., Sun, Y., Dai, X., Tang, C., Hu, C.: Evaluation of magnetic coupler for stationary EVs’ wireless charging. Int. J. Appl. Electromagn. Mech. 53(1), 167–179 (2017). https://doi.org/10.3233/JAE-160032
Jeong, S., Jang, Y.J., Kum, D.: Economic analysis of the dynamic charging electric vehicle. IEEE Trans. Power Electron. 30(11), 6368–6377 (2015). https://doi.org/10.1109/TPEL.2015.2424712
Ko, Y.D., Oh, Y.: Efficient deployment design of wireless charging electric tram system with battery management policy. Sustain. 12(7), (2020). https://doi.org/10.3390/su12072920
Jang, Y.J., Suh, E.S., Kim, J.W.: System architecture and mathematical models of electric transit bus system utilizing wireless power transfer technology. IEEE Syst. J. 10(2), 495–506 (2016). https://doi.org/10.1109/JSYST.2014.2369485
Jang, Y.J., Ko, Y.D., Jeong, S.: Optimal design of the wireless charging electric vehicle. In: 2012 IEEE international electric vehicle conference, IEVC 2012 (2012)
Ko, Y.D., Jang, Y.J.: The Parameter Design of the Wireless Power Electric Vehicle. In: IEEE Vehicular Technology Conference (2014)
Lee, M.S., Jang, Y.J.: Charging Infrastructure Allocation for Wireless Charging Transportation System. In: Proceedings of the Eleventh International Conference on Management Science and Engineering Management. pp. 1630–1644. Springer International Publishing (2018)
Mouhrim, N., El Hilali Alaoui, A., Boukachour, J.: Optimal allocation of wireless power transfer system for electric vehicles in a multipath environment. Proc. 3rd IEEE Int. Conf. Logist. Oper. Manag. GOL 2016. (2016). https://doi.org/10.1109/GOL.2016.7731684
Miller, J.M., Jones, P.T., Li, J.M., Onar, O.C.: ORNL experience and challenges facing dynamic wireless power charging of EV’s. IEEE Circuits Syst. Mag. 15(2), 40–53 (2015). https://doi.org/10.1109/MCAS.2015.2419012
Shin, S., Shin, J., Kim, Y., Lee, S., Song, B., Jung, G., Jeon, S.: Hybrid inverter segmentation control for online electric vehicle. In: 2012 IEEE international electric vehicle conference, IEVC 2012 (2012)
Lee, H., Ji, D., Cho, D.H.: Optimal design of wireless charging electric bus system based on reinforcement learning. Energies. 12(7), (2019). https://doi.org/10.3390/en12071229
Sagaama, I., Kchiche, A., Trojet, W., Kamoun, F.: Impact of Road Gradient on Electric Vehicle Energy Consumption in Real-World Driving. In: Advances in Intelligent Systems and Computing. pp. 393–404 (2020)
Multon, B., Hirsinger, L.: Problème de la motorisation d’un véhicule électrique. In: Journées de la section électrotechnique du club EEA 1994. p. 22p. (1994)
Posdijk, W., Dekker, P., Steinert-Threlkeld, S., Szymanik, J., Aloni, M., Zuidema, J.: The Influence of the Simplicity/Informativeness Trade-off on the Sematic Typology of Quantifiers. (2019)
Subashini, G., Bhuvaneswari, M.C.: Comparison of multi-objective evolutionary approaches for task scheduling in distributed computing systems. Sadhana Acad. Proc. Eng. Sci. 37(6), 675–694 (2012). https://doi.org/10.1007/s12046-012-0102-4
Deb, K., Pratap, A., Agarwal, S., Meyarivan, T.: A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 6(2), 182–197 (2002). https://doi.org/10.1109/4235.996017
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1 Linearization of the constraints (17) and (18) using the indicator constraints
The following constraints replaces the constraint (17). For this, we integrate the following binary variable \( {z}_{ij}^{l_p} \)
We apply the same procedure for the constraint (18)
Appendix 2 Coding of the nonlinear constraint (12)
forall(i in 0..I, j in 0..N-Lmax)
(if) (aij = 1)
{
for (var k = 0; k < Lm; k++)
(if) \( {\displaystyle \begin{array}{c}\left({z}_{ij}^k==k+1\right)\\ {}{y}_{ij}^{k0}=1-{S}_{i\left(j-1\right)}^0;\end{array}} \)
ilse
(if) \( {\displaystyle \begin{array}{c}\left({w}_{ij}^k==k+1\right)\\ {}{y}_{ij}^{k0}=1-{S}_{i\left(N-j+1\right)}^0;\end{array}} \)
else
}
}
Rights and permissions
About this article
Cite this article
Elbaz, ., Elhilali Alaoui, A. Optimal Installation of the Power Transmitters in the Dynamic Wireless Charging for Electric Vehicles in a Multipath Network with the Round-Trip Case. Int. J. ITS Res. 20, 46–63 (2022). https://doi.org/10.1007/s13177-021-00270-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13177-021-00270-5