Retailer’s optimal replenishment policy in a two-echelon supply chain under two-part delay in payments and disruption in delivery

Abstract

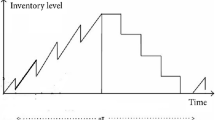
Now-a-days, the risks associated with transportation have received special attention among the global traders due to the unusual circumstances such as terrorist attack, earth quake, mishandling in transport, shipping damage, misplacing products etc. A mathematical model for an inventory system under such transport risk conditions is highly useful to run the supply chain (SC) smoothly and it paves the way to minimize the total cost incurred. In business, many suppliers offer two-part delay in payments, say $(\alpha /M_{1} ,{\text{ net }}M_{2} )$, in order to attract their retailers. This paper investigates retailer’s inventory system in a SC under the random effect of risk in delivery from a supplier to the retailer. Here, the supplier offers two-part trade credit to his retailer and the retailer in turn offers a full credit period to the customers. The total cost incurred at the retailer’s inventory system is minimized and the optimal replenishment policies are determined. Mathematical theorems are developed and numerical examples are presented to illustrate the sensitivity analysis of inventory key parameters.

Appendix 1

1.1 Proof of Theorem 1

Before going to the proof for the statements in Theorem 1, we need the following as a preliminary.

We could observe that $\frac{{d^{2} TC_{Ai} (T)}}{{dT^{2} }} > 0$ for i = 1, 2, 3, 4 under various conditions. So,

• (i) $\frac{{dTC_{A1} (T)}}{dT}$ is an increasing function on $[PM_{1} /\lambda ,\infty )$.

• (ii) $\frac{{dTC_{A2} (T)}}{dT}$ is an increasing function on $\left[ {M_{1} ,\frac{{PM_{1} }}{\lambda }} \right]$.

• (iii) $\frac{{dTC_{A3} (T)}}{dT}$ is an increasing function on $\left[ {M_{1} - N,M_{1} } \right]$.

$2A \ge \delta_{1}$ is implied from $T_{A1}^{*} \ge \frac{{PM_{1} }}{\lambda }$. Since $\frac{{dTC_{A1} (T)}}{dT}$ is an increasing function, we have $\frac{{dTC_{A1} (T_{A1}^{*} )}}{dT} \ge \frac{{dTC_{A1} (PM_{1} /\lambda )}}{dT}$. This implies that $\frac{{dTC_{A1} (PM_{1} /\lambda )}}{dT} \, \le 0$. Hence, $2A \ge \delta_{1}$ implies that $\frac{{dTC_{A1} (PM_{1} /\lambda )}}{dT} \, \le 0$ and so $2A \le \delta_{1}$ implies that $\frac{{dTC_{A1} (PM_{1} /\lambda )}}{dT} \, \ge 0.$ Similarly, $2A \ge \delta_{2}$ implies that $\frac{{dTC_{A2} (M_{1} )}}{dT} \, \le 0$ and so $2A \le \delta_{2}$ implies that $\frac{{dTC_{A2} (M_{1} )}}{dT} \, \ge 0.$

$2A \le \delta_{1}$ implies that $\frac{{dTC_{A2} (PM_{1} /\lambda )}}{dT} \, \ge 0$ and so $2A \ge \delta_{1}$ implies that $\frac{{dTC_{A2} (PM_{1} /\lambda )}}{dT} \, \le 0.$

$2A \le \delta_{2}$ implies that $\frac{{dTC_{A3} (M_{1} )}}{dT} \, \ge 0$ and so $2A \ge \delta_{2}$ implies that $\frac{{dTC_{A3} (M_{1} )}}{dT} \, \le 0.$

$2A \ge \delta_{3}$ implies that $\frac{{dTC_{A3} (M_{1} - N)}}{dT} \, \le 0$ and so $2A \le \delta_{3}$ implies that $\frac{{dTC_{A3} (M_{1} - N)}}{dT} \, \ge 0.$

$2A < \delta_{3}$ implies that $\frac{{dTC_{A4} (M_{1} - N)}}{dT} \, \ge 0$ and so $2A > \delta_{3}$ implies that $\frac{{dTC_{A4} (M_{1} - N)}}{dT} \, \le 0.$

• (a) If $2A \ge \delta_{1},$ then $TC_{A1} (T)$ is a convex function on $[PM_{1} /\lambda ,\infty )$ and $\frac{{dTC_{A1} (PM_{1} /\lambda )}}{dT} \, \le 0;$ This shows that $TC_{A1} (T)$ is decreasing on $[PM_{1} /\lambda ,T_{A1}^{*} ]$ and increasing on $[T_{A1}^{*} ,\infty ).$ Since $\delta_{1} \ge \delta_{2} \ge \delta_{3} \, ,$ we have $2A \ge \delta_{2}$ and $2A \ge \delta_{3}.$ These imply that $\frac{{dTC_{A2} (M_{1} )}}{dT} \, \le 0$ and $\frac{{dTC_{A3} (M_{1} )}}{dT} \, \le 0,$ $\frac{{dTC_{A3} (M_{1} - N)}}{dT} \, \le 0$ and $\frac{{dTC_{A4} (M_{1} - N)}}{dT} \, \le 0.$ $2A \ge \delta_{1}$ implies that $\frac{{dTC_{A2} (PM_{1} /\lambda )}}{dT} \, \le 0.$ Hence, we have (i) $TC_{A2} (T)$ is a decreasing function on $\left[ {M_{1} ,\frac{{PM_{1} }}{\lambda }} \right],$ (ii) $TC_{A3} (T)$ is a decreasing function on $\left[ {M_{1} - N,M_{1} } \right],$ (iii) $TC_{A4} (T)$ is a decreasing function on $\left[ {0,M_{1} - N} \right]$ since $\mathop { \lim }\limits_{{{\text{T}} \to 0}} TC_{A4}^{\prime } (T) = - \infty.$ Hence, $TC_{A} (T)$ is decreasing on [0, $T_{A1}^{*}$] and increasing on [$T_{A1}^{*}$,∞). Hence, $T^{*} = T_{A1}^{*}$ and $TC_{A}^{*} (T) = TC_{A1}^{*} (T_{A1}^{*} ).$

• (b) Let $\delta_{1} \ge 2A \ge \delta_{2}$. $\delta_{1} \ge 2A$ implies that $\frac{{dTC_{A1} (PM_{1} /\lambda )}}{dT} \, \ge 0$ and $\frac{{dTC_{A2} (PM_{1} /\lambda )}}{dT} \, \ge 0.$ $\delta_{2} \le 2A$ implies that $\frac{{dTC_{A2} (M_{1} )}}{dT} \, \le 0$ and $\frac{{dTC_{A3} (M_{1} )}}{dT} \, \le 0.$ $\delta_{3} \le \delta_{2} \le 2A$ implies that $\frac{{dTC_{A3} (M_{1} - N)}}{dT} \, \le 0$ and $\frac{{dTC_{A4} (M_{1} - N)}}{dT} \, \le 0.$ Since $TC_{A1}^{\prime } (T)$ is increasing on $[PM_{1} /\lambda ,\infty )$ and $\frac{{dTC_{A1} (PM_{1} /\lambda )}}{dT} \, \ge 0$ implies that $TC_{A1} (T)$ is increasing on $[PM_{1} /\lambda ,\infty ).$ Since $\delta_{1} \ge 2A \ge \delta_{2}$ implies that $TC_{A2} (T)$is a convex function on $[M_{1} ,PM_{1} /\lambda ]$ and $\frac{{dTC_{A2} (PM_{1} /\lambda )}}{dT} \, \ge 0$ and $\frac{{dTC_{A2} (M_{1} )}}{dT} \, \le 0.$ Therefore, $TC_{A2} (T)$ is decreasing on $[M_{1} ,T_{A2}^{*} ]$ and increasing on $[T_{A2}^{*} ,PM_{1} /\lambda ].$ Since $\frac{{dTC_{A3} (M_{1} )}}{dT} \, \le 0$ and $\frac{{dTC_{A3} (M_{1} - N)}}{dT} \, \le 0,$ $TC_{A3} (T)$ is decreasing on $\left[ {M_{1} - N,M_{1} } \right].$ Since $- \infty = \mathop { \lim }\limits_{{{\text{T}} \to 0}} TC_{A4}^{\prime } (T) < TC_{A4}^{\prime } (M_{1} - N) \le 0,$ $TC_{A4} (T)$ is decreasing on $\left[ {0,M_{1} - N} \right].$ Hence, $TC_{A} (T)$ is decreasing on [0, $T_{A2}^{*}$] and increasing on [$T_{A2}^{*}$, ∞). Hence, $T^{*} = T_{A2}^{*}$ and $TC_{A}^{*} (T) = TC_{A2}^{*} (T_{A2}^{*} ).$

• (c) Let $\delta_{2} \ge 2A \ge \delta_{3}.$ $\delta_{2} \ge 2A$ implies that $\delta_{1} \ge 2A.$ $\delta_{1} \ge 2A$ implies that $\frac{{dTC_{A1} (PM_{1} /\lambda )}}{dT} \, \ge 0$ and $\frac{{dTC_{A2} (PM_{1} /\lambda )}}{dT} \, \ge 0.$ $\delta_{2} \ge 2A$ implies that $\frac{{dTC_{A2} (M_{1} )}}{dT} \, \ge 0$ and $\frac{{dTC_{A3} (M_{1} )}}{dT} \, \ge 0.$ $2A \ge \delta_{3}$ implies that $\frac{{dTC_{A3} (M_{1} - N)}}{dT} \, \le 0$ and $\frac{{dTC_{A4} (M_{1} - N)}}{dT} \, \le 0.$ From the discussions in (b), $TC_{A1} (T)$ is increasing on $[PM_{1} /\lambda ,\infty ).$ Since $\frac{{dTC_{A2} (M_{1} )}}{dT} \, \ge 0$ and $\frac{{dTC_{A2} (PM_{1} /\lambda )}}{dT} \, \ge 0,$ $TC_{A2} (T)$is increasing on $[M_{1} ,PM_{1} /\lambda ].$ Since $\delta_{2} \ge 2A \ge \delta_{3},$ $TC_{A3} (T)$ is convex on $\left[ {M_{1} - N,M_{1} } \right]$ and $\frac{{dTC_{A3} (M_{1} - N)}}{dT} \, \le 0,$ $\frac{{dTC_{A3} (M_{1} )}}{dT} \, \ge 0,$ $TC_{A3} (T)$ is decreasing on $[M_{1} - N,T_{A3}^{*} ]$ and increasing on $[T_{A3}^{*} ,M_{1} ].$ Since $- \infty = \mathop { \lim }\limits_{{{\text{T}} \to 0}} TC_{A4}^{\prime } (T) < TC_{A4}^{\prime } (M_{1} - N) \le 0,$ $TC_{A4} (T)$ is decreasing on $\left[ {0,M_{1} - N} \right].$ Hence, $TC_{A} (T)$ is decreasing on [0, $T_{A3}^{*}$] and increasing on [$T_{A3}^{*}$, ∞). Hence, $T^{*} = T_{A3}^{*}$ and $TC_{A}^{*} (T) = TC_{A3}^{*} (T_{A3}^{*} )$

• (d) Let $\delta_{3} \ge 2A.$ Since $\delta_{1} \ge \delta_{2} \ge \delta_{3},$ we have the following

  (i) $\delta_{1} \ge 2A$ implies that $\frac{{dTC_{A1} (PM_{1} /\lambda )}}{dT} \, \ge 0$ and $\frac{{dTC_{A2} (PM_{1} /\lambda )}}{dT} \, \ge 0.$

  (ii) $\delta_{2} \ge 2A$ implies that $\frac{{dTC_{A2} (M_{1} )}}{dT} \, \ge 0$ and $\frac{{dTC_{A3} (M_{1} )}}{dT} \, \ge 0.$

  (iii) $\delta_{3} \ge 2A$ implies that $\frac{{dTC_{A3} (M_{1} - N)}}{dT} \, \ge 0$ and $\frac{{dTC_{A4} (M_{1} - N)}}{dT} \, \ge 0.$

  (iv) $TC_{A4} (T)$ is a convex function on $\left[ {0,M_{1} - N} \right].$

Therefore,

• (i) $TC_{A1} (T)$ is increasing on $[PM_{1} /\lambda ,\infty ).$

• (ii) $TC_{A2} (T)$ is increasing on $[M_{1} ,PM_{1} /\lambda ].$

• (iii) $TC_{A3} (T)$ is increasing on $[M_{1} - N,M_{1} ].$

• (iv) $TC_{A4} (T)$ is decreasing on $[0,T_{A4}^{*} ]$ and decreasing on $[T_{A4}^{*} ,M_{1} - N].$

Hence $TC_{A} (T)$ is decreasing on [0, $T_{A4}^{*}$] and increasing on [$T_{A4}^{*}$, ∞). Hence, $T^{*} = T_{A4}^{*}$ and $TC_{A}^{*} (T) = TC_{A4}^{*} (T_{A4}^{*} )$.