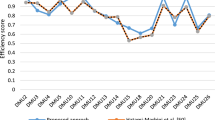
Abstract
DEA is a non-parametric technique for measuring the relative technical efficiencies of similar decision making units (DMUs) with multiple inputs and multiple outputs. In smoe real life situations, DMUs may perform different types of functions and can be segregated into independent components such that each component has its own set of inputs and outputs. Owing the importance of the internal structure of the DMUs, DEA has been extended to multi-component DEA (MC-DEA) which is a technique for measuring the technical efficiencies of the DMUs and their components. The conventional DEA and MC-DEA approaches require crisp input and output data which may not always be available precisely. However, in real life problems, data might be imprecise or vague which can suitably be represented by fuzzy numbers. Many researchers have proposed methods to deal with fuzzy parameters in DEA and MC-DEA. However, in real situations, the decision variables can also take fuzzy forms. Therefore, the aim of the present paper is fourfold: (i) to extend DEA in the presence of undesirable outputs to fully fuzzy DEA (FFDEA) for measuring the fuzzy technical efficiencies of the DMUs in fully fuzzy environments where all decision variables and parameters are taken as fuzzy numbers, in particular triangular fuzzy numbers, (ii) to extend MC-DEA in the presence of undesirable outputs to multi-component fully fuzzy DEA (MC-FFDEA) for measuring the fuzzy technical efficiencies of DMUs and their components in fully fuzzy environments, (iii) to propose a new ranking function approach to transform both the FFDEA and MC-FFDEA models into crisp linear programming problems, and (iv) to present numerical examples in order to validate the effectiveness and advantages of the proposed approach over the existing ones.



Similar content being viewed by others
References
Angiz LMZ, Emrouznejad A, Mustafa A (2012) Fuzzy data envelopment analysis: a discrete approach. Expert Syst Appl 39:2263–2269
Ashrafi A, Jaafar AB (2011) Efficiency measurement of series and parallel production systems with interval data by data envelopment analysis. Aust J Basic Appl Sci 5(11):1435–1443
Charnes A, Cooper WW, Rhodes E (1978) Measuring the efficiency of decision making units. Eur J Oper Res 2:429–444
Chen SM (1994) Fuzzy system reliability analysis using fuzzy number arithmetic operations. Fuzzy Sets Syst 66:31–38
Chen Y, Du J, Sherman HD, Zhu J (2010) DEA model with shared resources and efficiency decomposition. Eur J Oper Res 207:339–349
Cook WD, Green RH (2004) Multicomponent efficiency measurement and core business identification on multiplant firms: a DEA model. Eur J Oper Res 157:540–551
Cook WD, Roll Y (1993) Partial efficiencies in data envelopment analysis. Socio-Econ Plan Sci 37(3):171–179
Cook WD, Hababou M, Tuenter HJH (2000) Multicomponent efficiency measurement and shared inputs in DEA: an application to sales and service performance in bank branches. J Prod Anal 14:209–224
Cook WD, Zhu J, Bi GB, Yang F (2010) Network DEA: additive efficiency decomposition. Eur J Oper Res 207:1122–1129
Cooper WW, Seiford LM, Tone K (2007) Data envelopment analysis: a comprehensive text with models, applications, references and DEA-solver software, 2nd edn. Springer, New York
Emrouznejad A, Tavana M, Hatami-Marbini A (2014) The state of the art in fuzzy data envelopment analysis. In: Emrouznejad A, Tavana M (eds) Performance measurement with fuzzy data envelopment analysis, vol 309. Springer, Berlin, pp 1–45
Eslami GR, Mehralizadeh M, Jahanshahloo GR (2009) Efficiency measurement of multi-component decision making units using data envelopment analysis. Appl Math Comput 3(52):2575–2594
Färe R, Grosskopf S (1996) Productivity and intermediate products: a frontier approach. Econ Lett 50(1):65–70
Färe R, Grosskopf S (2004) Modeling undesirable factors in efficiency evaluation: comment. Eur J Oper Res 157:242–245
Färe R, Grabowski R, Grosskopf S, Kraft S (1997) Efficiency of a fixed but allocatable input: a non-parametric approach. Econ Lett 56:187–193
Guo P, Tanaka H (2001) Fuzzy DEA: a perceptual evaluation method. Fuzzy Sets Syst 119:149–160
Hatami-Marbini A, Emrouznejad A, Tavana M (2011a) A taxonomy and review of the fuzzy data envelopment analysis literature: two decades in the making. Eur J Oper Res 214:457–472
Hatami-Marbini A, Tavana M, Ebrahimi A (2011b) A fully fuzzified data envelopment analysis model. Int J Inf Decis Sci 3(3):252–264
Hosseinzadeh Lotfi F, Vaez-Ghasemi M (2013) Multi-component efficiency with shared resources in commercial banks. Int J Appl Oper Res 3(4):93–104
Jahanshahloo GR, Amirteimoori AR, Kordrostami S (2004a) Multi-component performance, progress and regress measurement and shared inputs and outputs in DEA for panel data: an application in commercial bank branches. Appl Math Comput 151:1–16
Jahanshahloo GR, Amirteimoori AR, Kordrostami S (2004b) Measuring the multi-component efficiency with shared inputs and outputs in data envelopment analysis. Appl Math Comput 155:283–293
Jahanshahloo GR, Hosseinzadeh Lotfi F, Shoja N, Tohidi G, Razavyan S (2005) Undesirable inputs and outputs in DEA models. App Math Comput 169:917–925
Jahanshahloo GR, Hosseinzadeh Lotfi F, Maddahi R, Jafari Y (2012) Efficiency and benchmarking in the presence of undesirable (bad) outputs: a DEA approach. Int J Appl Math Res 1(2):178–188
Kao C (2009a) Efficiency decomposition in network data envelopment analysis: a relational model. Eur J Oper Res 192:949–962
Kao C (2009b) Efficiency measurement for parallel production systems. Eur J Oper Res 196:1107–1112
Kao C (2012) Efficiency decomposition for parallel production systems. J Oper Res Soc 63:64–71
Kao C (2014a) Efficiency decomposition for general multi-stage systems in data envelopment analysis. Eur J Oper Res 232:117–124
Kao C (2014b) Network data envelopment analysis: a review. Eur J Oper Res 239:1–16
Kao C, Liu ST (2000) Fuzzy efficiency measures in data envelopment analysis. Fuzzy Sets Syst 113:427–437
Kazemi M, Alimi A (2014) A fully fuzzy approach to data envelopment analysis. J Math Comput Sci 11:238–245
Kordrostami S, Amirteimoori A (2005) Un-desirable factors in multi-component performance measurement. App Math Comput 171:721–729
León T, Liern V, Ruiz JL, Sirvent I (2003) A fuzzy mathematical programming approach to the assessment of efficiency with DEA models. Fuzzy Sets Syst 139:407–419
Lertworasirikul S, Fang SC, Joines JA, Nuttle HLW (2003) Fuzzy data envelopment analysis (DEA): a possibility approach. Fuzzy Sets Syst 139:379–394
Lewis HF, Sexton TR (2004) Network DEA: efficiency analysis of organizations with complex internal structure. Comput Oper Res 31:1365–1410
Liu WB, Meng W, Li XX, Zhang DQ (2010) DEA models with undesirable inputs and outputs. Ann Oper Res 173(1):177–194
Maleki HR (2002) Ranking functions and their applications to fuzzy linear programming. Far East J Math Sci 4:283–301
Park KS, Park K (2009) Measurement of multiperiod aggregative efficiency. Eur J Oper Res 193:567–580
Puri J, Yadav SP (2013) A concept of fuzzy input mix-efficiency in fuzzy DEA and its application in banking sector. Expert Syst Appl 40:1437–1450
Puri J, Yadav SP (2014) A fuzzy DEA model with undesirable fuzzy outputs and its application to the banking sector in India. Expert Syst Appl 41:6419–6432
Ramli NA, Munisamy S (2013) Modeling undesirable factors in efficiency measurement using data envelopment analysis: a review. J Sustain Sci Manag 8(1):126–135
Saati S, Memariani A, Jahanshahloo GR (2002) Efficiency analysis and ranking of DMUs with fuzzy data. Fuzzy Optim Decis Mak 1:255–267
Scheel H (2001) Undesirable outputs in efficiency valuations. Eur J Oper Res 132(2):400–410
Seiford L, Zhu J (2002) Modeling undesirable factors in efficiency evaluation. Eur J Oper Res 142(1):16–20
Sengupta JK (1992) A fuzzy systems approach in data envelopment analysis. Comput Math Appl 24(9):259–266
Shen Y, Ruan D, Hermans E, Brijs T, Wets G, Vanhoof K (2011) Modeling qualitative data in data envelopment analysis for composite indicators. Int J Syst Assur Eng Manag 2(1):21–30
Shiraz RK, Charles V, Jalalzadeh L (2014) Fuzzy rough DEA model: a possibility and expected value approaches. Expert Syst Appl 41:434–444
Tone K, Tsutsui M (2009) Network DEA: a slacks-based measure approach. Eur J Oper Res 197:243–252
Triantis K, Girod O (1998) A mathematical programming approach for measuring technical efficiency in a fuzzy environment. J Prod Anal 10:85–102
Wang YM, Chin KS (2011) Fuzzy data envelopment analysis: a fuzzy expected value approach. Expert Syst Appl 38:11678–11685
Wang YM, Luo Y, Liang L (2009) Fuzzy data envelopment analysis based upon fuzzy arithmetic with an application to performance assessment of manufacturing enterprising. Expert Syst Appl 36:5205–5211
Wei QL, Yan H, Pang LY (2011) Composite network data envelopment analysis model. Int J Inf Technol Decis Making 10:613–633
Yang Y, Ma B, Koike M (2000) Efficiency-measuring DEA model for production system with k independent subsystems. J Oper Res Soc Jpn 43:343–354
Zadeh LA (1965) Fuzzy sets. Inf Control 8:338–353
Zimmermann HJ (1996) Fuzzy set theory and its applications, 3rd edn. Kluwer-Nijhoff Publishing, Boston
Acknowledgments
The authors are thankful to the anonymous reviewer for the constructive comments and suggestions that helped us in improving the paper significantly. The first author is also thankful to the University Grants Commission (UGC), Government of India, New Delhi for financial assistance.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Puri, J., Yadav, S.P. A fully fuzzy approach to DEA and multi-component DEA for measuring fuzzy technical efficiencies in the presence of undesirable outputs. Int J Syst Assur Eng Manag 6, 268–285 (2015). https://doi.org/10.1007/s13198-015-0348-4
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13198-015-0348-4