Skip to main content
SpringerLink
Log in

Exploration of reliability algorithms using modified Weibull distribution: application on gas turbine

  • Case Study
  • Published:
International Journal of System Assurance Engineering and Management Aims and scope Submit manuscript

Abstract

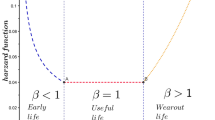
The main purpose of the present paper is the exploration of an algorithm for reliability assessment and analysis based on the modified Weibull distribution. Indeed, an original methodology for the monitoring and the evaluation of the a gas turbine system reliability has been proposed and set up. The obtained results in this work show the effectiveness of the used approach for assessing the operational reliability (observed and estimated) for the studied system by providing advantageous performance in minimizing the number of data classes. On the other side; these results allow a better understanding of the studied system behavior based on its reliability and survival function analyzing. Finally, the validation tests on heavily biased data and on incomplete data confirm the effectiveness of the proposed algorithm.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  • Ahmadi MV, Doostparast M, Ahmadi J (2013) Estimating the lifetime performance index with Weibull distribution based on progressive first-failure censoring scheme. J Comput Appl Math 239(1):93–102

    Article  MATH  MathSciNet  Google Scholar 

  • Almalki SJ, Yuan J (2013a) The new modified Weibull distribution. Reliab Eng Syst Saf 111:164–170

    Article  Google Scholar 

  • Almalki SJ, Yuan J (2013b) A new modified Weibull distribution. Reliab Eng Syst Saf 111(1):164–170

    Article  Google Scholar 

  • Ascher H (1981). Weibull distribution vs Weibull process. In: Annual reliability and maintainability symposium, pp 426–431

  • Ascher H, Feingold H (1984) Repairable systems modelling, inferences, misconceptions and their causes. Marcel Decker, New York

    MATH  Google Scholar 

  • Bain LJ, Engelhardt M, Wright FT (1984) Tests for an increasing trend in the intensity of a Poisson process: a power study. J Am Stat Assoc 390:419–423

    Google Scholar 

  • Barabadi A (2013) Reliability model selection and validation using Weibull probability plot—a case study. Electr Power Syst Res 101(1):96–101

    Article  Google Scholar 

  • Djeddi AZ, Hafaifa A, Salam A (2015) Gas turbine reliability model based on tangent hyperbolic reliability function. J Theor Appl Mech 53(3):723–730

    Article  Google Scholar 

  • Ebeling CE (2010) An introduction to reliability and maintainability engineering. Tata McGraw-Hill Education, Newyork

    Google Scholar 

  • Fei CW, Tang WZ, Bai GC (2014) Novel method and model for dynamic reliability optimal design of turbine blade deformation. Aerosp Sci Technol 39:588–595

    Article  Google Scholar 

  • Freedman D, Diaconis P (1981) On the histogram as a density estimator: L 2 theory. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete 57(4):453–476

    Article  MATH  MathSciNet  Google Scholar 

  • Garmabaki AHS, Ahmadi A, Mahmood YA, Barabadi A (2015) Reliability modelling of multiple repairable units. Qual Reliab Eng Int. doi:10.1002/qre.1938

    Google Scholar 

  • Guemana M, Hafaifa A, Rahmoune MB (2015) Reliability study of gas turbines for improving their availability by ensuring optimal exploitation. Oil Gas Eur Mag 2:88–91

    Google Scholar 

  • Hafaifa A, Belhadef R, Guemana M (2013) Reliability model exploitation in industrial system maintainability using expert system evaluation. In: Proceedings of the 4th international conference on integrity, reliability and failure, IRF2013, June 2013, Funchal, Madeira, Portugal, pp 387–388

  • Hafaifa A, Guemana M, Daoudi A (2015) Vibration supervision in gas turbine based on parity space approach to increasing efficiency. J Vib Control 21:622–1632

    Article  Google Scholar 

  • Hasumi T, Akimoto T, Aizawa Y (2009) The Weibull–log Weibull distribution for interoccurrence times of earthquakes. Phys A 388(4):491–498

    Article  Google Scholar 

  • Kumar U, Klefsjo B (1992) Reliability analysis of hydraulic systems of LHD machines using the power law process model. Reliab Eng Syst Saf 35:217–224

    Article  Google Scholar 

  • Lai CD (1994) Tests of univariate and bivariate stochastic ageing. IEEE Trans Reliab 43(2):233–241

    Article  Google Scholar 

  • Lai CD, Moore T, Xie M (1998) The beta integrated model. In: Prococeding of the international workshop on reliability modeling and analysis: from theory to practice, pp 153–159

  • Lai CD, Xie M, Murthy DNP (2003) A modified Weibull distribution. IEEE Trans Reliab 52(1):33–37

    Article  Google Scholar 

  • Liu W, Li J (2012) An improved cut-based recursive decomposition algorithm for reliability analysis of networks. Earthq Eng Eng Vib 11(1):1–10

    Article  Google Scholar 

  • Moeini A, Jenab K, Mohammadi M, Foumani M (2013) Fitting the three-parameter Weibull distribution with cross entropy. Appl Math Model 37(9):6354–6363

    Article  MathSciNet  Google Scholar 

  • Nadarajah S, Kotz S (2008) Strength modeling using Weibull distributions. J Mech Sci Technol 22(7):1247–1254

    Article  Google Scholar 

  • Nadarajah S, Cordeiro GM, Ortega EMM (2013) The exponentiated Weibull distribution: a survey. Stat Pap 54(3):839–877

    Article  MATH  Google Scholar 

  • Need R, Rampersad V, Riverol C (2015) Reliability evaluation of a gas turbine water wash system–a case study. J Nat Gas Sci Eng 24:457–463

    Article  Google Scholar 

  • Pham H, Lai CD (2007) On recent generalizations of the Weibull distribution. IEEE Trans Reliab 56(3):454–458

    Article  Google Scholar 

  • Rausand M, Høyland A (2004) System reliability theory: models, statistical methods, and applications. Wiley, Hoboken

    MATH  Google Scholar 

  • Rigdon SE (2002) Properties of the Duane plot for repairable systems. Qual Reliab Eng Int 18(1):1–4

    Article  Google Scholar 

  • Rigdon SE, Basu AP (2000) Statistical methods for the reliability of repairable systems. John Wiley, New York

    MATH  Google Scholar 

  • Sarhan AM, Apaloo J (2013) Exponentiated modified Weibull extension distribution. Reliab Eng Syst Saf 112:137–144

    Article  Google Scholar 

  • Scott DW (1979) On optimal and data-based histograms. Biometrika 66(3):605–610

    Article  MATH  MathSciNet  Google Scholar 

  • Shmueli G, Jank W, Hyde V (2008) Transformations for semi-continuous data. Comput Stat Data Anal 52(8):4000–4020

    Article  MATH  MathSciNet  Google Scholar 

  • Silva GO, Ortega EMM, Cancho VG (2010) Log-Weibull extended regression model: estimation, sensitivity and residual analysis. Stat Methodol 7(6):614–631

    Article  MATH  MathSciNet  Google Scholar 

  • Sturges H (1926) The choice of a class-interval. J Amer Statist Assoc 21: 65–66

    Article  Google Scholar 

  • Tsoutsanis E, Meskin N, Benammar M, Khorasani K (2016) A dynamic prognosis scheme for flexible operation of gas turbines. Appl Energy 164(15):686–701

    Article  Google Scholar 

  • Yang J, Scott DW (2013) Robust fitting of a Weibull model with optional censoring. Comput Stat Data Anal 67(1):149–161

    Article  MathSciNet  Google Scholar 

  • Zare V (2016) Exergoeconomic analysis with reliability and availability considerations of a nuclear energy-based combined cycle power plant. Energy 96:187–196

    Article  Google Scholar 

  • Zhu SP, Huang HZ, Peng W, Wang HK, Mahadevan S (2016) Probabilistic physics of failure-based framework for fatigue life prediction of aircraft gas turbine discs under uncertainty. Reliab Eng Syst Saf 146:1–12

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Applied Automation and Industrial Diagnostics Laboratory, Faculty of Science and Technology, University of Djelfa, 17000, Djelfa, Algeria

    Ahmed Zohair Djeddi, Ahmed Hafaifa & Abdellah Kouzou

  2. Faculty of Science and Technology, University of Medea, 26000, Medea, Algeria

    Salam Abudura

Authors
  1. Ahmed Zohair Djeddi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ahmed Hafaifa
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Abdellah Kouzou
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Salam Abudura
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ahmed Hafaifa.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Djeddi, A.Z., Hafaifa, A., Kouzou, A. et al. Exploration of reliability algorithms using modified Weibull distribution: application on gas turbine. Int J Syst Assur Eng Manag 8 (Suppl 2), 1885–1894 (2017). https://doi.org/10.1007/s13198-016-0480-9

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13198-016-0480-9

Keywords

Search

Navigation