Abstract
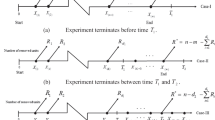
The life data analysis has been finding increasing importance for every industry, resulting in higher quality and cost reduction in current fierce competitive market. The hazard function for life models have three distinct phases of burn-in, useful life and wear-out shown in the bath-tub curves. Change points estimation is important for bathtub-shaped hazard function models in reliability and life data analysis for the product developer and designers to have a relatively accurate estimation of the burn-in, useful life and onset of the wear-out life phases. The applications are for determination and assisting to plan appropriate burn-in, guarantee, maintenance, repair and replacement strategies. In this research, life time interval is studied for bathtub shaped hazard function. Two change points are calculated for burn-in and useful life phases, as well as useful life and wear out phases. Two criteria are used in this study for determination of the change point including (1) minimum of hazard function and (2) maximum change in slope of hazard function. This research is structured as a parametric approach with Bayesian inference utilized as the parameter estimation. The modified Weibull distribution are determined as the suitable models for simulation of all three life phases. In this paper, failure data of an electronic system case is used for the method demonstration.




Similar content being viewed by others
Abbreviations
- \( {\text{t}}_{\text{i}} \) :
-
Time to failure (h)
- \( \alpha \) :
-
Scale parameter
- \( \beta \) :
-
Shape parameter
- λ:
-
Shape parameter
- \( {\text{h}}\left( {\text{t}} \right) \) :
-
Hazard function
- \( \delta \) :
-
Significant confidence area
- \( {\text{a}}_{\text{i}} \) :
-
Uniform distribution first parameter
- \( {\text{b}}_{\text{i}} \) :
-
Uniform distribution second parameter
- \( \bar{h} \) :
-
Estimated value of h
- σ :
-
Standard deviation
- K–S:
-
Kolmogorov–Smirnov
References
Aarest MV (1987) How to identify a bathtub hazard rate. IEEE Trans Reliab 36:106–108
Almalki SJ, Nadarjah S (2014) Modification of the Weibull distribution: a review. Reliab Eng Syst Saf 124:32–55
Almalki SJ, Yuan J (2013) The new modified Weibull distribution. Reliab Eng Syst Saf 111:164–170
Basu AP, Ghosh JK, Joshi SN (1988) On estimating change point in a failure rate, statistical decision theory and related topics IV, 2nd edn. Springer, NewYork, pp 239–252
Bebbington M, Lai CD, Wellington M, Zitikis R (2007) A flexible Weibull extension. Reliab Eng Syst Saf 92:719–726
Bebbington M, Lai CD, Wellington M, Zitikis R (2008) Estimating the turning point of a bathtub-shaped failure distribution. J Stat Plan Inference 138:1157–1166
Bebbington M, Lai CD, Wellington M, Zitikis R (2012) The discrete additive Weibull distribution: a bathtub shaped hazard for discontinuous failure data. Reliab Eng Syst Saf 106:37–44
Chen Z, Ferger D, Mi J (2001) Estimation of the change point of a distribution based on the number of failed test items. Metrika 53:31–38
Cooray K (2006) Generalization of the Weibull distribution: the odd Weibull family. Stat Model 6:265–277
Ghosh JK, Joshi SN (1992) On the asymptotic distribution of an estimate of the change point in a failure rate. Comm Stat Theory Methods 21:3571–3588
Ghosh JK, Joshi SN, Mukhopadhayay C (1993) A Bayesian approach to the estimation of change point in a hazard rate. Advances in reliability. Elsevier, Amsterdam, pp 141–170
Ghosh JK, Joshi SN, Mukhopadhyay C (1996) Asimptotics of a Bayesian approach to estimating change-point in a hazard rate. Commun Stat Theory Methods 25:3147–3166
Joshi SN, MacEachrrn SN (1997) Isotonic maximum likelihood estimation for the change point of a hazard rate. Sankhya Ser A 59:392–407
Karasoy D, Kadilar C (2009) Modified estimators for the change point in hazard function. J Comput Appl Math 229:152–157
Kulasekera KB, Lal Saxena KM (1991) J Stat Plan Inference 29:111–124
Lai CD, Xie M, Murthy DNP (2003) A modified Weibull distribution. IEEE Trans Reliab 52:33–37
Mudholkar GS, Kollia GD (1994) Generalized Weibull family: a structural analysis. Commun Stat Theory Methods 23:1149–1171
Mudholkar GS, Srivastava DK (1993) Exponentiated Weibull family for analyzing bathtub failure-rate data. IEEE Trans Reliab 42:299–302
Mudholkar GS, Srivastava DK, Freimer M (1995) The exponentiated Weibull family: a reanalysis of the bus-motor-failuredata. Technometrics 37:436–445
Mudholkar GS, Srivastava DK, Kollia GD (1996) A generalization of the weibull distribution with application to the analysis of survival data. J Am State Assoc 91:1575–1583
Murari M, Basu SK (1995) Change point estimation in non-monotonic aging models. Ann Inst Statist Math 47(3):483–491
Nguyen HT, Rogers GS, Walker EA (1984) Estimation in change-point hazard rate models. Biometrika 71:299–304
Nooghabi MS, Borzadaran GRM, Roknabadi AHR (2011) Discrete modified Weibull distribution. Metron 69:207–222
Pham TD, Ngunyen HT (1990) Strong consistency of the maximum likelihood estimators in the change point hazard rate model. Statistics 21:203–216
Pham TD, Ngunyen HT (1993) Bootstrapping the change point of a hazard rate models. Biometrika 71:299–304
Xie M, Lai C (1996) Reliability analysis using an additive Weibull model with bathtub-shaped failure rate function. Reliab Eng Syst Saf 52:87–93
Xie M, Tang Y, Goh TN (2002) A modified Weibull extension with bathtub shaped failure rate function. Reliab Eng Syst 7:279–285
Yao YC (1986) Maximum likelihood estimation in hazard rate models with a change-point. Commun Stat Theory Methods 15:2455–2466
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Aghazadeh Chakherloo, R., Pourgol-Mohammad, M. & Sepanloo, K. Change points estimations of bathtub-shaped hazard functions. Int J Syst Assur Eng Manag 8, 553–559 (2017). https://doi.org/10.1007/s13198-016-0567-3
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13198-016-0567-3