Abstract
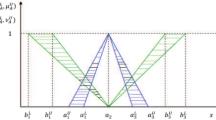
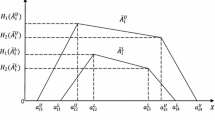
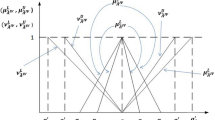
In decision making of real life two stage time minimizing transportation problem (TSTMTP), we face here the state of uncertainty as well as hesitation due to some uncontrollable factors. Many authors have used fixed or fuzzy data in TSTMTP. But, TSTMTP with uncertainty and hesitation cannot be solved properly by taking fixed or fuzzy data. In present article, we have considered TSTMTP with uncertainty and hesitation of supply, demand and time. Here we have made decision of real life TSTMTP with uncertainty and hesitation by using triangular intuitionistic fuzzy numbers (TIFNs). We have generalized expected interval and value of triangular fuzzy numbers for TIFNs which converts each TIFN to a real number, also proposed and proved some related results. Further, a method is presented for the solution of real life TSTMTP and degrees of acceptance and rejection of optimal decision are computed by using generalized Zadeh’s extension principle. Finally, proposed method is implemented in an example.

Similar content being viewed by others
References
Aizemberg L, Kramer HH, Pessoa AA, Uchoa E (2014) Formulations for a problem of petroleum transportation. Eur J Oper Res 237:82–90
Atanassov T (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20:87–96
Atony RJP, Savarimuthu SJ, Pathinathan T (2014) Method for solving the transporation problem using triangular intutitionistic fuzzy number. Int J Comput Algorithm 03:590–605
Bellman RE, Zadeh LA (1970) Decision making in a fuzzy environment. Manag Sci 17:B141–B164
Christi AK, Kumari S (2015) Two stage fuzzy transportation problem using symmetric trapezoidal fuzzy number. Int J Eng Invent 4:7–10
Das SK, Goswami A, Alam AA (1999) Multiobjective transportation problem with interval cost, source and destination parameters. Eur J Oper Res 117:100–112
Dinagar DS, Thiripurasundari K (2014) A novel method for solving fuzzy transporation problem involving intuitionistic fuzzy trapezoidal fuzzy numbers. Int J Curr Res 6:7038–7041
Gani AN, Razak KA (2006) Two stage fuzzy transportation problem. J Phys Sci 10:63–69
Gulati TR, Rani D, Kumar A (2014) A method for unbalanced transportation problems in fuzzy environment. Sadhana 39:573–581
Heilpern S (1992) The expected value of a fuzzy number. Fuzzy Sets Syst 47(1):81–86
Hitchcock FL (1941) The distribution of a product from several sources to numerous localities. J Math Phys 20:224–230
Kaur P, Dahiya K (2015) Two-stage interval time minimization transportation problem with capacity constraints. Innov Syst Des Eng 6:79–85
Kumar A, Gupta A (2011) A new method for solving linear multi-objective transportation problems with fuzzy parameters. Appl Math Model 36:1421–1430
Li L, Lai KK (2000) A fuzzy approach to the multiobjective transportation problem. Comput Oper Res 27:43–57
Maleki HR, Zangiabadi M (2007) Fuzzy goal programming for multiobjective transporation problems. J Appl Math Comput 24:449–460
Marinov E (2014) On extension principle for intuitionistic fuzzy sets. Notes Intuit Fuzzy Sets 20:34–41
Ritha W, Vinotha J (2009) Merline: multi-objective two stage fuzzy transportation problem. J Phys Sci 13:107–120
Sharma A, Verma V, Kaur P, Dahiya K (2015) An iterative algorithm for two level hierarchical time minimization transportation problem. Eur J Oper Res 000:1–8
Singh SK, Yadav SP (2015) Efficient approach for solving type-1 intuitionistic fuzzy transportation problem. Int J Syst Assur Eng Manag 6:259–267
Sonia, Malhotra R (2003) A polynomial algorithm for a two stage time minimising transportation problem. Opsearch 39:251–266
Sudhakar VK, Kumar NV (2011) A different approach for solving two stage fuzzy transportation problems. Int J Contemp Math Sci 6:517–526
Wahed W, Lee SM (2006) Interactive fuzzy goal programming for multi-objective transportation problems. Omega 34:158–166
Zadeh LA (1965) Fuzzy sets. Inf Control 8:338–353
Zimmermann HJ (1978) Fuzzy programming and linear programming with several objective functions. Fuzzy Sets Syst 1:45–55
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Bharati, S.K., Malhotra, R. Two stage intuitionistic fuzzy time minimizing transportation problem based on generalized Zadeh’s extension principle. Int J Syst Assur Eng Manag 8 (Suppl 2), 1442–1449 (2017). https://doi.org/10.1007/s13198-017-0613-9
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13198-017-0613-9