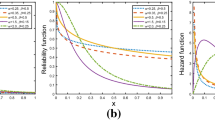
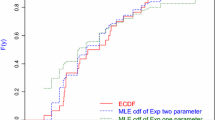
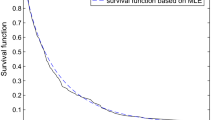
Abstract
This article deals with the classical and Bayesian estimation of the parameters of log-logistic distribution using random censorship model. The maximum likelihood estimators and the asymptotic confidence intervals based on observed Fisher information matrix of the parameters are derived. Bayes estimators of the parameters under generalized entropy loss function using independent gamma priors are obtained. For Bayesian computation, Tierney–Kadane’s approximation and Markov chain Monte Carlo (MCMC) methods are used. Also, the highest posterior credible intervals of the parameters based on MCMC method are constructed. A Monte Carlo simulation study is carried out to compare the behavior of various estimators developed in this article. Finally, a real data analysis is performed for illustration purposes.




Similar content being viewed by others
References
Abbas K, Tang Y (2016) Objective Bayesian analysis for log-logistic distribution. Commun Stat Simul Comput 45(8):2782–2791
Akaike H (1974) A new look at the statistical models identification. IEEE Trans Autom Control 19(6):716–723
Al-Shomrani AA, Shawky AI, Arif OH, Aslam M (2016) Log-logistic distribution for survival data analysis using MCMC. SpringerPlus 5(1774):1–16
Ameraouia A, Boukhetala K, Dupuy J-F (2016) Bayesian estimation of the tail index of a heavy tailed distribution under random censoring. Comput Stat Data Anal 104:148–168
Arnold BC, Press SJ (1983) Bayesian inference for Pareto populations. J Econom 21:287–306
Breslow N, Crowley J (1974) A large sample study of the life table and product limit estimates under random censorship. Ann Stat 2(3):437–453
Calibra R, Pulcini G (1996) Point estimation under asymmetric loss functions for life truncated exponential samples. Commun Stat Theory Methods 25(3):585–600
Chen Z (2006) Estimating the shape parameter of the log-logistic distribution. Int J Reliab Qual Saf Eng 13(3):257–266
Chen MH, Shao QM (1999) Monte Carlo estimation of Bayesian credible and HPD intervals. J Comput Graph Stat 8(1):69–92
Danish MY, Aslam M (2013) Bayesian estimation for randomly censored generalized exponential distribution under asymmetric loss functions. J Appl Stat 40(5):1106–1119
Danish MY, Aslam M (2014) Bayesian inference for the randomly censored Weibull distribution. J Stat Comput Simul 84(1):215–230
Dube M, Garg R, Krishna H (2016) On progressively first failure censored Lindley distribution. Comput Stat 31(1):139–163
Garg R, Dube M, Kumar K, Krishna H (2016) On randomly censored generalized inverted exponential distribution. Am J Math Manag Sci 35(4):361–379
Ghitany ME (2001) A compound Rayleigh survival model and its applications to randomly censored data. Stat Pap 42:437–450
Gilbert JP (1962) Random censorship. Ph.D. thesis, University of Chicago
Hastings WK (1970) Monte Carlo sampling methods using Markov chains and their applications. Biometrika 57:97–109
Kantam RRL, Rosaiah K, Srinivasa Rao G (2001) Acceptance sampling based on life test: log-logistic model. J Appl Stat 28(1):121–128
Kantam RRL, Srinivasa Rao G, Sriram B (2006) An economic reliability test plan: log-logistic distribution. J Appl Stat 33(3):291–296
Kaplan EL, Meier P (1958) Nonparametric estimation from incomplete observations. J Am Stat Assoc 53:457–481
Koziol JA, Green SB (1976) A Cramer-von Mises statistic for randomly censored data. Biometrika 63(3):465–474
Krishna H, Goel N (2017) Classical and Bayesian inference in two parameter exponential distribution with randomly censored data. Comput Stat. https://doi.org/10.1007/s00180-017-0725-3
Krishna H, Vivekanand, Kumar K (2015) Estimation in Maxwell distribution with randomly censored data. J Stat Comput Simul 85(17):3560–3578
Kumar K, Krishna H, Garg R (2015) Estimation of P(Y < X) in Lindley distribution using progressively first failure censoring. Int J Syst Assur Eng Manag 6(3):330–341
Kumar K, Garg R, Krishna H (2017) Nakagami distribution as a reliability model under progressive censoring. Int J Syst Assur Eng Manag 8(1):109–122
Kuş CS, Kaya MF (2006) Estimation of parameters of the Log-logistic distribution based on progressive censoring using the EM algorithm. Hacet J Math Stat 35(2):203–211
Lawless JF (2003) Statistical models and methods for lifetime data. Wiley, NewYork
Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E (1953) Equations of state calculations by fast computing machines. J Chem Phys 21:1087–1092
Mudholkar GS, Srivastava DK, Kollia GD (1996) A generalization of the Weibull distribution with application to the analysis of survival data. J Am Stat Assoc 91:1575–1583
Robert CP, Casella G (2004) Monte Carlo Statistical methods, 2nd edn. Springer, NewYork
Roberts GO, Smith AFM (1993) Bayesian computation via the Gibbs sampler and related Markov chain Monte Carlo methods. J R Stat Soc B 55(1):3–23
Saleem M, Aslam M (2009) On Bayesian analysis of the Rayleigh survival time assuming the random censor time. Pak J Sci 25(2):71–82
Schwarz G (1978) Estimating the dimension of a model. Ann Stat 6(2):421–464
Shah BK, Dave PH (1963) A note on log-logistic distribution. J Math Sci Univ Baroda (Science Number) 12:21–22
Tierney T, Kadane JB (1986) Accurate approximations for posterior moments and marginal densities. J Am Stat Assoc 81:82–86
Acknowledgements
The author expresses his sincere thanks to anonymous reviewers for their constructive comments and useful suggestions which led to improvement in the quality of this article.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Kumar, K. Classical and Bayesian estimation in log-logistic distribution under random censoring. Int J Syst Assur Eng Manag 9, 440–451 (2018). https://doi.org/10.1007/s13198-017-0688-3
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13198-017-0688-3