Abstract
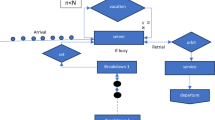
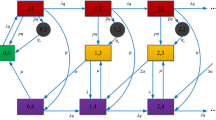
The paper investigates the M/M/s retrial queueing system with servers prone to breakdown and with voluntary service. During a phone call, if the caller finds a free call line, then it connects immediately to the call agent, considered as server. Those who finds the call busy either join the orbit for retrial or disconnect the call. After receiving the essential service either caller leaves the system or requests for voluntary service. The miniature used in the queueing system employs a quasi-birth-and-death process. The stationary probabilities are derived using matrix-analytic approach and then performance measures are calculated using these stationary probabilities. The impact of system parameters on performance measures is illustrated using graphs and tables. Total system cost is calculated as a function of orbit capacity, repair rate of breakdown and two different service rates. The optimization methodology is demonstrated using various cases. Further the Genetic algorithm is used to find the optimum value of both essential and optional service rates, rate of breakdown and orbit capacity to minimize the overall cost. The study of consistency of retrial queue with server prone to breakdowns and repairs is of great significance because of inadequate capability of repairs and strong impact of the breakdowns on the performance measures.









Similar content being viewed by others
References
Ahuja A, Jain A, Jain M (2019) Finite population multi-server retrial queueing system with an optional service and balking. Int J Comput Appl 41(1):53–60
Alkaff A, Qomarudin MN, Wiratno SE (2020) Matrix-analytic solutions in production lines without buffers. Comput Oper Res. https://doi.org/10.1016/j.cor.2020.104903
Chakravarthy SR, Kulshrestha R (2020) A queueing miniature with server breakdowns, repairs, vacations, and backup server. Oper Res Perspect. https://doi.org/10.1016/j.orp.2019.100131
Chang FM, Ke JC (2009) On a batch retrial miniature with J vacations. J Comput Appl Math 232(2):402–414. https://doi.org/10.1016/j.cam.2009.06.033
Chang FM, Liu TH, Ke JC (2018) On an unreliable-server retrial queue with customer feedback and impatience. Appl Math Miniat 55:171–182
Dimitriou I (2018) A two-class queueing system with constant retrial policy and general class dependent service times. Eur J Oper Res 270(3):1063–1073
Dudin AN, Dudin SA, Dudina OS, Samouylov KE (2020) Competitive queueing systems with comparative rating dependent arrivals. Oper Res Perspect. https://doi.org/10.1016/j.orp.2020.100139
Falin G (1990) A survey of retrial queues. Queueing Syst 7:127–167. https://doi.org/10.1007/BF01158472
Falin GI, Artalejo JR (1998) A finite source retrial queue. Eur J Oper Res 108(2):409–424
Gao S, Zhang D (2020) Performance and sensitivity analysis of an M/G/1 queue with retrial customers due to server vacation. Ain Shams Eng J 11(3):795–803
Gharbi N, Dutheillet C (2011) An algorithmic approach for analysis of finite-source retrial systems with unreliable servers. Comput Math Appl 62(6):2535–2546
Goldberg DE (1989) Genetic algorithms in search, optimization, and machine learning, Boston, MA: Addison-Wesley. ISBN: 978-0-201-15767-3
Gross D, Shortle JF, Thompson JM, Harris CM (2008) Fundamentals of queueing theory. John Wiley & Sons, Hoboken, NJ. https://doi.org/10.1002/9781118625651
Guo H (2012) Application of genetic algorithms in the new air traffic management simulation system. Phys Proc 33:604–611
Hu L, Jiang Y, Zhu J, Chen Y (2015) A PH/PH (n)/C/C state-dependent queueing miniature for metro station corridor width design. Eur J Oper Res 240(1):109–126. https://doi.org/10.1016/j.ejor.2014.06.010
Jahedsani H, Azimi P (2018) Optimizing a hierarchical location: allocation problem using the M/M/M queue miniature and solving it employing a genetic algorithm. Ind Eng Manag. https://doi.org/10.4172/2169-0316.1000267.
Jain M, Kumar P, Meena RK (2020) Fuzzy metrics and cost optimization of a fault-tolerant system with vacationing and unreliable server. J Ambient Intell Humaniz Comput 11:5755–5770. https://doi.org/10.1007/s12652-020-01951-x
Jain M, Shekhar C, Meena RK (2019) Performance analysis and control F-Policy for fault-tolerant system with working vacation. OPSEARCH 56:409–431
Kawanishi K (2008) QBD approximations of a call center queueing miniature with general patience distribution. Comput Oper Res 35(8):2463–2481. https://doi.org/10.1016/j.cor.2006.12.002
Ke JC, Chang FM (2009) Modified vacation policy for M/G/1 retrial queue with balking and feedback. Comput Ind Eng 57(1):433–443. https://doi.org/10.1016/j.cie.2009.01.002
Ke JB, Ke JC, Lin CH (2010) Cost optimization of an M/M/r queueing system with queue-dependent servers: genetic algorithm. In: Proceedings of the 5th international conference on queueing theory and network applications, pp 82–86
Ke JC, Wu CH, Pearn WL (2011) Multi-server retrial queue with second optional service: algorithmic computation and optimisation. Int J Syst Sci 42(10):1755–1769
Kumar P, Jain M, Meena RK (2021) Optimal control of fault tolerant machining system with reboot and recovery in fuzzy environment using harmony search algorithm. ISA Trans. ISSN 0019-0578. https://doi.org/10.1016/j.isatra.2021.02.027
Lan S, Tang Y (2020) An unreliable discrete-time retrial queue with probabilistic pre-emptive priority, balking customers and replacements of repair times. AIMS Math 5(5):4322–4344
Liou CD (2015) Markovian queue optimisation analysis with an unreliable server subject to working breakdowns and impatient customers. Int J Syst Sci 46(12):2165–2182. https://doi.org/10.1080/00207721.2013.859326
Liou CD, Wang KH, Liou MW (2013) Genetic algorithm to the machine repair problem with two removable servers operating under the triadic (0, Q, N, M) policy. Appl Math Miniat 37(18–19):8419–8430. https://doi.org/10.1016/j.apm.2013.03.036
Jain M, Meena R (2017) Markovian analysis of unreliable multi-components redundant fault tolerant system with working vacation and F-policy. Cogent Math 4:1–17
Markova E, Satin Y, Kochetkova I, Zeifman A, Sinitcina A (2020) Queuing system with unreliable servers and inhomogeneous intensities for analyzing the impact of non-stationarity to performance measures of wireless network under licensed shared access. Mathematics. https://doi.org/10.3390/MATH8050800
Meena RK, Jain M, Sanga SS, Assad A (2019) Fuzzy miniatureling and harmony search optimization for machining system with general repair, standby support and vacation. Appl Math Comput 361:858–873
Morozov E, Rumyantsev A, Dey S, Deepak TG (2019) Performance analysis and stability of multiclass orbit queue with constant retrial rates and balking. Perform Eval. https://doi.org/10.1016/j.peva.2019.102005
Mukeba Kanyinda JP, Mabela Makengo Matendo R, Ulungu Ekunda Lukata B (2015) Computing fuzzy queueing performance measures by L-R method. J Fuzzy Set Valued Anal 1:57–67. https://doi.org/10.5899/2015/jfsva-00226
Phung-Duc T, Kawanishi K (2014) Performance analysis of call centers with abandonment, retrial, and after-call work. Perform Eval 80:43–62
Sanga SS, Jain M (2019a) FM/FM/1 double orbit retrial queue with customers’ joining strategy: a parametric nonlinear programming approach. Appl Math Comput. https://doi.org/10.1016/j.amc.2019.06.056
Sanga SS, Jain M (2019b) Cost optimization and ANFIS computing for admission control of M/M/1/K queue with general Retrial times and discouragement. Appl Math Comput. https://doi.org/10.1016/j.amc.2019.124624
Sethi R, Jain M, Meena RK (2021) Markov model for fault tolerant machining system operating under admission control policy. Proc Natl Acad Sci India Sect A Phys Sci. https://doi.org/10.1007/s40010-021-00734-z
Shin YW, Choo TS (2009) M/M/s queue with impatient customers and retrials. Appl Math Miniat 33(6):2596–2606. https://doi.org/10.1016/j.apm.2008.07.018
Singh CJ, Jain M, Kaur S (2018) Performance analysis of bulk arrival queue with balking, optional service, delayed repair, and multi-phase repair. Ain Shams Eng J 9(4):2067–2077
Wang K-H, Chen W-L, Yang D-Y (2009) Optimal management of the machine repair problem with working vacation: Newton’s method. J Comput Appl Math 233:449–458
Funding
There was no funding obtained in this research.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Human or Animal rights
No animals and human participants data used in this research article.
Informed consent
We give consent for this publication.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Jain, M., Jain, A. Genetic algorithm in retrial queueing system with server breakdown and caller intolerance with voluntary service. Int J Syst Assur Eng Manag 13, 582–598 (2022). https://doi.org/10.1007/s13198-021-01364-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13198-021-01364-9