Skip to main content
Springer Nature Link
Log in

Order diminution and its application in controller design using salp swarm optimization technique

  • Original article
  • Published:
International Journal of System Assurance Engineering and Management Aims and scope Submit manuscript

Abstract

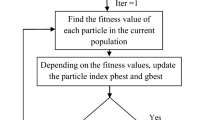
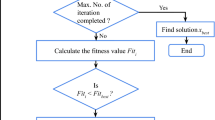
Order diminution (OD) or model order reduction (MOR), a very important field of System Engineering, has been explored by many researchers. Different methods are available for reducing the complexity of a control system, which are subsequently utilized to get a cost-effective controller. Model order reduction is done by either using classical methods or by using optimization techniques. In optimization algorithms, accuracy, complexity, and convergent rate are the main criteria for comparison in OD. This paper contributes a novel fast and more accurate OD (MOR) technique based on Salp Swarm Optimization. Further, the proposed method is applied to a time-delay system in four different manners. The effectiveness of the proposed technique is shown by reducing four benchmark systems, including a system with time delay and an 84th order system. Finally, the application of OD is shown by designing a reduced-based H-infinity controller for the 84th order system which results in a great saving of time (\(\approx 96\%\)). The obtained results are comparable or better than those from the existing well-known order reduction techniques available in the literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  • Abdullah Hadeel N (2019) A hybrid bacterial foraging and modified particle swarm optimization for model order reduction. Int J Elect Comput Eng (IJECE) 9(2):1100–1109

    Article  Google Scholar 

  • Abu-Al-Nadi Dia, Alsmadi Othman MK, Abo-Hammour Zaer S (2011) Reduced order modeling of linear mimo systems using particle swarm optimization. In The seventh international conference on Autonomic and Autonomous Systems (ICAS 2011), pages 3–7, 2011

  • Afzal Sikander, Rajendra B, Prasad. (2015) A novel order reduction method using cuckoo search algorithm. IETE J Res 61(2):83–90

    Article  Google Scholar 

  • Ahamad Nafees, Sikander Afzal, Singh Gagan (2019) Substructure preservation based approach for discrete time system approximation. Microsyst Technol 25(2):641–649

    Article  Google Scholar 

  • Ahamad Nafees, Singh Gagan, Khan Shahala, Sikander Afzal (2017) Design and performance analysis of optimal reduced order h-infinity controller: L1 norm based genetic algorithm technique. In 2017 International Conference on Power and Embedded Drive Control (ICPEDC), pages 8-13. IEEE, 2017

  • Bhaumik Adrish, Kumar Yashwant, Srivastava Saurabh, Islam Sk Mafizul (2016) Performance studies of a separately excited dc motor speed control fed by a buck converter using optimized pi\(lambda\)d\(mu\) controller. pp 1–6

  • Biradar Shivanagouda, Hote Yogesh V, Saxena Sahaj (2016) Reduced-order modeling of linear time invariant systems using big bang big crunch optimization and time moment matching method. Appl Math Model 40(15–16):7225–7244

    Article  MathSciNet  Google Scholar 

  • Chahlaoui Younes, Van Dooren Paul (2005) Benchmark examples for model reduction of linear time-invariant dynamical systems. Dimension Reduction of Large-Scale Systems. Springer, Berlin Heidelberg, pp 379–392

  • Desai SR, Rajendra Prasad (2013) A novel order diminution of lti systems using big bang big crunch optimization and routh approximation. Appl Math Modelling 37(16–17):8016–8028

    Article  MathSciNet  Google Scholar 

  • Eitelberg E (1981) Model reduction by minimizing the weighted equation error. Int J Control 34(6):1113–1123

    Article  MathSciNet  Google Scholar 

  • Eitelberg E (1982) Comments on model reduction by minimizing the equation error. IEEE Trans Autom Control 27(4):1000–1002

    Article  MathSciNet  Google Scholar 

  • El-Attar R, Vidyasagar M (1978) Order reduction by l-1-and l-infinity-norm minimization. IEEE Trans Autom Control 23(4):731–734

    Article  Google Scholar 

  • Gahinet Pascal, Apkarian Pierre (1994) A linear matrix inequality approach to h-infinity control. Int J Robust Nonlin Cont 4(4):421–448

    Article  Google Scholar 

  • Ganguli Souvik, Kaur Gagandeep, Sarkar Prasanta (2018) A hybrid intelligent technique for model order reduction in the delta domain: a unified approach. Soft Comput pp 1–14

  • Garg Harish (2016) A hybrid pso-ga algorithm for constrained optimization problems. Appl Math Comput 274:292–305

    MathSciNet  MATH  Google Scholar 

  • Garg Harish (2019) A hybrid gsa-ga algorithm for constrained optimization problems. Inf Sci 478:499–523

    Article  Google Scholar 

  • Garg Harish (2015) A hybrid ga-gsa algorithm for optimizing the performance of an industrial system by utilizing uncertain data. In Handbook of research on artificial intelligence techniques and algorithms, pages 620–654. IGI Global, 2015

  • Golberg David E (1989) Genetic algorithms in search, optimization, and machine learning. Addion wesley 1989(102):36

    Google Scholar 

  • Kennedy James (2010) Particle swarm optimization. Encyclopedia of machine learning. pp 760–766

  • Mirjalili Seyedali, Gandomi Amir H, Mirjalili Seyedeh Zahra (2017) Shahrzad Saremi, Hossam Faris, and Seyed Mohammad Mirjalili. Salp swarm algorithm: A bio-inspired optimizer for engineering design problems. Adv Eng Softw 114:163–191

    Article  Google Scholar 

  • Parmar G, Prasad R, Mukherjee S (2007) Order reduction of linear dynamic systems using stability equation method and ga. Int J Comput Inf Syst Sci Eng 1(1):26–32

    Google Scholar 

  • Philip Boby, Pal Jayanta (2010) An evolutionary computation based approach for reduced order modelling of linear systems. pp 1–8

  • Prajapati Arvind Kumar, Prasad Rajendra (2019) Order reduction in linear dynamical systems by using improved balanced realization technique. Circuits, Systems, and Signal Processing 1–15

  • Rahimian Mohammad (2019) Measuring efficiency in dea by differential evolution algorithm. Ann Optimiz Theory Practice 2(1):19–26

    Google Scholar 

  • Rashid Pathan Siraj, Deepak Panwar (2020) A smart channel estimation approach for lte systems using pso algorithm. Ann Optimiz Theory Practice 3(3):1–13

    Google Scholar 

  • Sambariya DK, Omveer Sharma (2016) Model order reduction using routh approximation and cuckoo search algorithm. J Automat Cont 4(1):1–9

    Google Scholar 

  • Seok Lee Kang, Woo Geem Zong (2004) A new structural optimization method based on the harmony search algorithm. Comput Struct 82(9–10):781–798

    Google Scholar 

  • Sikander A (2016) Reduced order modelling for linear systems and controller design. Indian Institute of Technology Roorkee, Roorkee, India (PhD thesis)

    Google Scholar 

  • Sikander Afzal, Prasad Rajendra (2015) Linear time-invariant system reduction using a mixed methods approach. Appl Math Model 39(16):4848–4858

    Article  MathSciNet  Google Scholar 

  • Storn Rainer, Price Kenneth (1997) Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces. J Global Optim 11(4):341–359

    Article  MathSciNet  Google Scholar 

  • Vishwakarma CB, Prasad R (2008) Clustering method for reducing order of linear system using pade approximation. IETE J Res 54(5):326–330

    Article  Google Scholar 

  • White AS, Kelly C (1994) Optimization of a control algorithm using a simulation package. Microprocess Microsyst 18(2):89–94

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Electrical and Electronics and Communication Engineering Department, DIT University, Dehradun, India

    Nafees Ahamad & Gagan Singh

  2. Department of Instrumentation and Control Engineering, Dr. B. R. Ambedkar National Institute of Technology Jalandhar, Jalandhar, India

    Afzal Sikander

Authors
  1. Nafees Ahamad
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Afzal Sikander
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Gagan Singh
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Nafees Ahamad.

Ethics declarations

Funding

No funding was received to assist with the preparation of this manuscript.

Conflict of interest

The authors declare that they have no conflict of interest.

Availability of data and material

All data generated or analysed during this study are included in this published article.

Code availability

MarhWorks®

Ethics approval

Not applicable

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ahamad, N., Sikander, A. & Singh, G. Order diminution and its application in controller design using salp swarm optimization technique. Int J Syst Assur Eng Manag 13, 933–943 (2022). https://doi.org/10.1007/s13198-021-01367-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13198-021-01367-6

Keywords