Neutrosophic trade-credit EOQ model for deteriorating items considering expiration date of the items using different variants of particle swarm optimizations

Abstract

In reality, many businessmen often offer their products on delay or trade credit payments scheme to boost sales and diminish inventory. Trade credit financing plays a vital role in enabling retailers and customers to purchase goods without making prompt payments. As part of the trade credit financing scheme, the retailer receives an upstream trade credit from the supplier, while the retailer offers downstream trade credit to its customers. This paper proposes and explores an EOQ model involving an inventory-dependent demand and a trade credit scheme. In addition, expiration dates are taken into account when calculating the deterioration rate (e.g., various packaged food items, medicines, some cosmetic items etc.). As few parameters involve some sorts of uncertainty, we develop an imprecise and a crispified model in close parallel with the deterministic one. To represent this impreciseness in terms of linear trapezoidal neutrosophic fuzzy numbers (LTrNFN) as well as to crispify them, we use the removal area method. Then the crisp and crispified models are solved by using Weighted Quantum-Behaved Particle Swarm Optimization (WQPSO), Gaussian Quantum-Behaved Particle Swarm Optimization (GQPSO), and Adaptive Quantum-Behaved Particle Swarm Optimization (AQPSO), and the optimum profit is obtained from the best profit of these three algorithms. A number of numerical examples are presented in order to evaluate the validity of the proposed models and algorithms. Finally, the effects of changes of different inventory parameters involved in the crisp and crispified models are performed and some managerial insights are pointed out.

Appendix

1.1 A. Basic concepts of neutrosophic set

1.1.1 Neutrosophic Set (NSS)

Suppose $X$ be the space of points and let $x \in X,$ a neutrosophic set $\tilde{A}^{N}$ characterized by the truth membership function $\mu_{{\tilde{A}^{N} }} (x),$ non-membership function $\nu_{{\tilde{A}^{N} }} (x)$ and indeterminacy function $\xi_{{\tilde{A}^{N} }} (x)$ having the following form

$$\tilde{A}^{N} = \left\{ {(x,\mu_{{\tilde{A}^{N} }} (x),\nu_{{\tilde{A}^{N} }} (x),\xi_{{\tilde{A}^{N} }} (x)):x \in X} \right\}$$

where the above stated functions are standard or nonstandard subsets of $(0,1)$ that is $\mu_{{\tilde{A}^{N} }} (x):X \to (0^{ - } ,1^{ + } );\quad \nu_{{\tilde{A}^{N} }} (x):X \to (0^{ - } ,1^{ + } );\quad \xi_{{\tilde{A}^{N} }} (x):X \to (0^{ - } ,1^{ + } ).$

For the above functions, ${\text{sup}}\mu_{{\tilde{A}^{N} }} (x),{\text{ sup}}\nu_{{\tilde{A}^{N} }} (x),{\text{ sup}}\xi_{{\tilde{A}^{N} }} (x)$ the following inequality is satisfied

$$0^{ - } \le {\text{sup}}\mu_{{\tilde{A}^{N} }} (x) + {\text{sup}}\nu_{{\tilde{A}^{N} }} (x) + {\text{sup}}\xi_{{\tilde{A}^{N} }} (x) \le 3^{ + } .$$

From the definition it is evident that a neutrosophic set $\tilde{A}^{N}$ takes real value in $(0^{ - } ,1^{ + } )$ but in the present real scenario it is difficult to use the value from the set $(0^{ - } ,1^{ + } ).$

1.1.2 Trapezoidal neutrosophic number

Let $y$ be a Trapezoidal neutrosophic fuzzy number. Then its truth membership, indeterminacy membership and falsity membership functions are stated as follows:

$$T_{y} (p) = \left\{ {\begin{array}{*{20}l} {\frac{{\left( {p - a_{1}^{\prime } } \right)t_{y} }}{{\left( {a_{2}^{\prime } - a_{1}^{\prime } } \right)}},} \hfill & {a_{1}^{\prime } \le p \le a_{2}^{\prime } } \hfill \\ {t_{y} ,} \hfill & {a_{2}^{\prime } \le p \le a_{3}^{\prime } } \hfill \\ {\frac{{\left( {a_{4}^{\prime } - p} \right)t_{y} }}{{\left( {a_{4}^{\prime } - a_{3}^{\prime } } \right)}},} \hfill & {a_{3}^{\prime } \le p \le a_{4}^{\prime } } \hfill \\ {0,} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$

$$I_{y} (p) = \left\{ {\begin{array}{*{20}l} {\frac{{\left( {a_{2}^{\prime } - p} \right) + \left( {p - a_{1}^{\prime } } \right)i_{y} }}{{\left( {a_{2}^{\prime } - a_{1}^{\prime } } \right)}},} \hfill & {a_{1}^{\prime } \le p \le a_{2}^{\prime } } \hfill \\ {i_{y} ,} \hfill & {a_{2}^{\prime } \le p \le a_{3}^{\prime } } \hfill \\ {\frac{{(p - a_{3}^{\prime } ) + \left( {a_{4}^{\prime } - p} \right)i_{y} }}{{\left( {a_{4}^{\prime } - a_{3}^{\prime } } \right)}},} \hfill & {a_{3}^{\prime } \le p \le a_{4}^{\prime } } \hfill \\ {0,} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$

$$F_{y} (p) = \left\{ {\begin{array}{*{20}l} {\frac{{\left( {a_{2}^{\prime } - p} \right) + \left( {p - a_{1}^{\prime } } \right)f_{y} }}{{\left( {a_{2}^{\prime } - a_{1}^{\prime } } \right)}},} \hfill & {a_{1}^{\prime } \le p \le a_{2}^{\prime } } \hfill \\ {f_{y} ,} \hfill & {a_{2}^{\prime } \le p \le a_{3}^{\prime } } \hfill \\ {\frac{{(p - a_{3}^{\prime } ) + \left( {a_{4}^{\prime } - p} \right)f_{y} }}{{\left( {a_{4}^{\prime } - a_{3}^{\prime } } \right)}},} \hfill & {a_{3}^{\prime } \le p \le a_{4}^{\prime } } \hfill \\ {0,} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$

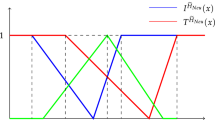
Here $0 \le T_{y} (p) \le 1,0 \le I_{y} (p) \le 1,0 \le F_{y} (p) \le 1\;{\text{and}}\;0 \le T_{y} (p) + I_{y} (p) + F_{y} (p) \le 1,\;a_{1}^{\prime } ,a_{2}^{\prime } ,a_{3}^{\prime } ,a_{4}^{\prime } \in R.$ Then $y = \left( {\left[ {a_{1}^{\prime } ,a_{2}^{\prime } ,a_{3}^{\prime } ,a_{4}^{\prime } } \right]:t_{y} ,i_{y} ,f_{y} } \right)$ is called the Trapezoidal neutrosophic fuzzy number (Fig. 21). 

Fig. 21

Trapezoidal neutrosophic fuzzy number

1.1.3 Single Valued Neutrosophic Set (SVNS)

A Single Valued Neutrosophic Set $\tilde{A}^{N}$ generated by the truth membership function $\mu_{{\tilde{A}^{N} }} (x),$ non-membership function $\nu_{{\tilde{A}^{N} }} (x)$ and indeterminacy function $\xi_{{\tilde{A}^{N} }} (x)$ has the following form $\tilde{A}^{N} = \left\{ {(x,\mu_{{\tilde{A}^{N} }} (x),\nu_{{\tilde{A}^{N} }} (x),\xi_{{\tilde{A}^{N} }} (x)):x \in X} \right\}$, where the above stated functions are standard or non-standard subsets of $(0,1)$ that is

$$\mu_{{\tilde{A}^{N} }} (x):X \to [0,1];\,\nu_{{\tilde{A}^{N} }} (x):X \to [0,1];\,\,\xi_{{\tilde{A}^{N} }} (x):X \to [0,1]$$

The functions $\mu_{{\tilde{A}^{N} }} (x), \, \nu_{{\tilde{A}^{N} }} (x), \, \xi_{{\tilde{A}^{N} }} (x)$ satisfy the following inequality

$$0 \le \mu_{{\tilde{A}^{N} }} (x) + \nu_{{\tilde{A}^{N} }} (x) + \xi_{{\tilde{A}^{N} }} (x) \le 3 \, \forall x \in X.$$

1.1.4 Single valued trapezoidal neutrosophic set (SVTNN)

A Single Valued Trapezoidal Neutrosophic number $\tilde{P}$ is defined as $\tilde{P} = \left( {\left[ {\left( {i_{1} ,i_{2} ,i_{3} ,i_{4} } \right);\rho } \right],\left[ {\left( {j_{1} ,j_{2} ,j_{3} ,j_{4} } \right);\sigma } \right],\left[ {\left( {k_{1} ,k_{2} ,k_{3} ,k_{4} } \right);\delta } \right];} \right),$ where $\rho ,\sigma ,\delta \in [0,1].$

The truth membership functions $(\mu_{{\tilde{P}}} ):{\mathbf{\mathbb{R}}} \to [0,\rho ]$, the non-membership function $(\nu_{{\tilde{P}}} ):{\mathbf{\mathbb{R}}} \to [\sigma ,1]$ and indeterminancy membership function $(\xi_{{\tilde{P}}} ):{\mathbf{\mathbb{R}}} \to [\delta ,1]$ are given as (Fig. 22): 

Fig. 22

Single valued trapezoidal neutrosophic set

:

$$\mu_{{_{{\tilde{P}}} }} (x) = \left\{ {\begin{array}{*{20}l} {\mu_{{_{{\tilde{P}l1}} }} (x),} \hfill & {i_{1} \le x \le i_{2} } \hfill \\ {\rho ,} \hfill & {i_{2} \le x \le i_{3} } \hfill \\ {\mu_{{_{{\tilde{P}l2}} }} (x){,}} \hfill & {i_{3} \le x \le i_{4} } \hfill \\ {0,} \hfill & {{\text{Otherwise}}} \hfill \\ \end{array} } \right\}{;}\quad \nu_{{_{{\tilde{P}}} }} (x) = \left\{ {\begin{array}{*{20}l} {\nu_{{_{{\tilde{P}l1}} }} (x),} \hfill & {j_{1} \le x \le j_{2} } \hfill \\ {\sigma ,} \hfill & {j_{2} \le x \le j_{3} } \hfill \\ {\nu_{{_{{\tilde{P}l2}} }} (x){,}} \hfill & {j_{3} \le x \le j_{4} } \hfill \\ {1,} \hfill & {{\text{Otherwise}}} \hfill \\ \end{array} } \right\};\quad \xi_{{_{{\tilde{P}}} }} (x) = \left\{ {\begin{array}{*{20}l} {\xi_{{_{{\tilde{P}l1}} }} (x),} \hfill & {k_{1} \le x \le k_{2} } \hfill \\ {\delta ,} \hfill & {k_{2} \le x \le k_{3} } \hfill \\ {\xi_{{_{{\tilde{P}l2}} }} (x),} \hfill & {k_{3} \le x \le k_{4} } \hfill \\ {1,} \hfill & {{\text{Otherwise}}} \hfill \\ \end{array} } \right\}$$

1.1.5 Crispification of neutrosophic trapezoidal fuzzy number using Removal Area Method

With the consideration of the assumptions mentioned in Sect. 2, first we formulate the crisp model in which all control parameters are taken as fixed real numbers. Then the neutrosophic fuzzy model is formulated taking the parameters as neutrosophic fuzzy numbers. This model is more realistic in terms uncertainties prevailed in the real life situation of the model. Thereafter, the crispified model is deduced in order to avoid the direct computational complexity of the neutrosophic model.

Let us consider a linear trapezoidal neutrosophic fuzzy number as follows (Fig. 23).

Fig. 23

Pictorial representation of neutrosophic trapezoidal fuzzy number

Let us consider a real number $p \in {\mathbf{\mathbb{R}}}{.}$ We also consider a fuzzy number $\tilde{A}$ associated with the lower trapezium, and then left hand side removal area of $\tilde{A}$ with respect to $p$ is $P_{l} (\tilde{A},p)$ and is defined as the area bounded by $p$ and the left hand side of the fuzzy number $\tilde{A}.$ Similarly, if we consider the right hand side removal of $\tilde{A}$ with respect to $p$ it will be $P_{r} (\tilde{A},p)$; we also consider a fuzzy number $\tilde{B}$ associated with the left most upper trapezium ( ABCD), then left hand side removal area of $\tilde{B}$ with respect to $p$ will be $P_{l} (\tilde{B},p),$ and is defined as the area bounded by r and the left side of the fuzzy number $\tilde{B}.$ Similarly, if we consider the right hand side removal area of $\tilde{B}$ with respect to $p$ it will be $P_{l} (\tilde{B},p),$ A fuzzy number $\tilde{C}$ associated with the right most upper trapezium ( STUV), then left side removal of $\tilde{C}$ with respect to $p$ is $P_{l} (\tilde{C},p),$ and is defined as the area bounded by r and the left hand side of the fuzzy number $\tilde{C}$. Finally, the right hand side removal of $\tilde{C}$ with respect to $p$ is $P_{r} (\tilde{C},p).$

The mean is defined as

$$\begin{gathered} P(\tilde{A},p) = \frac{{P_{l} (\tilde{A},p) + {\text{P}}_{r} (\tilde{A},p)}}{2}, \hfill \\ P(\tilde{B},p) = \frac{{P_{l} (\tilde{B},p) + {\text{P}}_{r} (\tilde{B},p)}}{2}, \hfill \\ P(\tilde{C},p) = \frac{{P_{l} (\tilde{C},p) + {\text{P}}_{r} (\tilde{C},p)}}{2}. \hfill \\ \end{gathered}$$

Then, we define the crispification of a linear neutrosophic trapezoidal fuzzy as:

$$P(\tilde{C}_{r} ,p) = \frac{{P(\tilde{A},p) + P(\tilde{B},p) + P(\tilde{C},p)}}{3}.$$

For $p = 0,$

$$P(\tilde{C}_{r} ,0) = \frac{{P(\tilde{A},0) + P(\tilde{B},0) + P(\tilde{C},0)}}{3}.$$

Let, $\tilde{A}_{tn} = \left( {a_{1} ,a_{2} ,a_{3} ,a_{4} ;b_{1} ,b_{2} ,b_{3} ,b_{4} ;c_{1} ,c_{2} ,c_{3} ,c_{4} } \right)$ be a linear neutrosophic trapezoidal fuzzy number.

$$P_{ \, l} (\tilde{A},0) = {\text{Area of trapezium OGHW}} = \frac{{(a_{1} + a_{2} )}}{2}.1$$

$$P_{ \, r} (\tilde{A},0) = {\text{Area of trapezium OJUW}} = \frac{{(a_{3} + a_{4} )}}{2}.1$$

$$P_{ \, l} (\tilde{B},0) = {\text{Area of trapezium OBAW}} = \frac{{(b_{1} + b_{2} )}}{2}.1$$

$$P_{ \, r} (\tilde{B},0) = {\text{Area of trapezium OCDW}} = \frac{{(b_{3} + b_{4} )}}{2}.1$$

$$P_{ \, l} (\tilde{C},0) = {\text{Area of trapezium OTSW}} = \frac{{(c_{1} + c_{2} )}}{2}.1$$

$$P_{ \, r} (\tilde{C},0) = {\text{Area of trapezium OUVW}} = \frac{{(c_{3} + c_{4} )}}{2}.1$$

Then, $P(\tilde{A},0) = \frac{{(a_{1} + a_{2} + a_{3} + a_{4} )}}{4},P(\tilde{B},0) = \frac{{(b_{1} + b_{2} + b_{3} + b_{4} )}}{4},P(\tilde{C},0) = \frac{{(c_{1} + c_{2} + c_{3} + c_{4} )}}{4}.$

Hence, $P(\tilde{C}_{r} ,0) = \frac{{a_{1} + a_{2} + a_{3} + a_{4} + b_{1} + b_{2} + b_{3} + b_{4} + c_{1} + c_{2} + c_{3} + c_{4} }}{12}.$