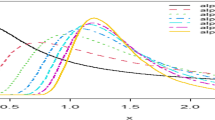
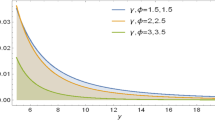
Abstract
If the items are very reliable, assessing the lifetime of them in regular usage requires more time and money than in accelerated conditions. As a result, life testing studies benefit greatly from accelerated life testing (ALT) since it saves time and money. In ALT, the components are subjected to higher levels of stress than usual in order to detect early failures in a short period of time and so decrease the expenses associated with component testing while maintaining quality. In this paper, a problem-based constant stress partially accelerated life test for multiple censored data is investigated. Under normal and accelerated settings, failure data from test objects is supposed to follow the Power Lindley distribution. The maximum likelihood estimates (MLEs) are obtained by solving the likelihood equations numerically. The approximate confidence intervals for the parameters are calculated using a normal approximation to the asymptotic distribution of MLEs. A simulation study is then used to test and validate the estimators' performance.








Similar content being viewed by others
References
Abushal TA, AL-Zaydi AM (2017) Inference on constant-partially accelerated life tests for mixture of pareto distributions under progressive type-II censoring. Open J Stat 7(02):323
Alam I, Ahmed A (2020) Parametric and interval estimation under step-stress partially accelerated life tests using adaptive type-II progressive hybrid censoring. Ann Data Sci. https://doi.org/10.1007/s40745-020-00249-1
Alam I, Ahmed A (2021) Inference on maintenance service policy under step-stress partially accelerated life tests using progressive censoring. J Stat Comput Simul. https://doi.org/10.1080/00949655.2021.1975282
Alam I, Islam AU, Ahmed A (2019) Parametric estimation on constant stress partially accelerated life tests for the exponentiated exponential distribution using multiple censoring. Reliab Theory Appl 14(4):20–31
Alam I, Islam A, Ahmed A (2020) Accelerated life test plans and age-replacement policy under warranty on burr type-X distribution with Type-II censoring. J Stat Appl Probab 9(3):515–524
Alam I, Intezar MA, Ahmed A (2021) Costs of maintenance service policy: a new approach on constant stress partially accelerated life test for generalized inverted exponential distribution. Reliab Theory Appl 16(2):45–57
Alam I, Haq A, Sharma LK, Sharma S (2023) Warranty costs analysis under accelerated life test for power Ishita distribution with type-I censored data. Int J Q Reliab Manag 40(8):1983–1998
Bader MG, Priest AM (1982) Statistical aspects of fiber and bundle strength in hybrid composites. In: Hayashi T, Kawata K, Umekawa S (eds), Progress in Science and Engineering Composites. ICCM-IV, Tokyo, pp 1129–1136
Bai DS, Chung SW (1992) Optimal design of partially accelerated life tests for the exponential distribution under type-I censoring. IEEE Trans Reliab 41(3):400–406
Bakouch HS, Al-Zahrani BM, Al-Shomrani AA, Marchi VA, Louzada F (2012) An extended Lindley distribution. J Korean Stat Soc 41(1):75–85
Cheng YF, Wang FK (2012) Estimating the Burr XII parameters in constant-stress partially accelerated life tests under multiple censored data. Commun Stat-Simul Comput 41(9):1711–1727
DeGroot MH, Goel PK (1979) Bayesian estimation and optimal designs in partially accelerated life testing. Naval Res Log Q 26(2):223–235
El-Din MM, Abu-Youssef SE, Ali NS, Abd El-Raheem AM (2016) Estimation in constant-stress accelerated life tests for extension of the exponential distribution under progressive censoring. Metron 74(2):253–273
EL-Sagheer RM, Khder MA (2021) Estimation in K-stage step-stress partially accelerated life tests for generalized pareto distribution with progressive type-I censoring. Appl Math Inf Sci 15(3):299–305
Ghitany ME, Al-Mutairi DK, Balakrishnan N, AlEnezi LJ (2013a) Power Lindley distribution and associated inference. Comput Stat Data Anal 64:20–33
Ghitany ME, Al-Mutairi DK, Balakrishnan N, Al-Enezi LJ (2013b) Power Lindley distribution and associated inference. Comput Stat Data Anal 64:20–33
Ghitany ME, Al-Mutairi DF, Aboukhamseen SM (2015) Estimation of the reliability of a stress–strength system from power Lindley distributions. Commun Stat Simul Comput 44(1):118–136
Guan Q, Tang Y, Fu J, Xu A (2014) Optimal multiple constant-stress accelerated life tests for generalized exponential distribution. Commun Stat-Simul Comput 43(8):1852–1865
Han D, Bai T (2020) Design optimization of a simple step-stress accelerated life test–contrast between continuous and interval inspections with non-uniform step durations. Reliab Eng Syst Saf 199:106875
Hassan AS, Assar MS, Zaky AN (2015) Constant-stress partially accelerated life tests for inverted Weibull distribution with multiple censored data. Int J Adv Stat Probab 3(1):72–82
Ismail AA (2016) Reliability analysis under constant-stress partially accelerated life tests using hybrid censored data from weibull distribution. Hacettepe J Math Stat 45(1):181–193
Kamal M (2013) Application of geometric process in accelerated life testing analysis with type-I censored weibull failure data. Reliab Theory Appl 8(3):87–96
Kamal M (2021) Parameter estimation for progressive censored data under accelerated life test with k levels of constant stress. Reliab Theory Appl 16(3):149–159
Kamal M, Zarrin S, Islam AU (2013) Constant stress partially accelerated life test design for inverted weibull distribution with type-I censoring. Algorithms Res 2(2):43–49
Kamal M, Zarrin S, Islam A (2014) Design of accelerated life testing using geometric process for type-II censored Pareto failure data. Int J Mathe Modell Comput 4(2):125–134
Kamal M, Rahman A, Ansari SI, Zarrin S (2020) Statistical analysis and optimum step stress accelerated life test design for nadarajah haghighi distribution. Reliab Theory Appl 15(4):1–9
Ling L, Xu W, Li M (2009) Parametric inference for progressive type-I hybrid censored data on a simple step-stress accelerated life test model. Math Comput Simul 79(10):3110–3121
Mahmoud MA, EL-Sagheer RM, Abou-Senna AM (2018) Estimating the modified weibull parameters in the presence of constant-stress partially accelerated life testing. J Stat Theory Appl 17(2):242–260
Meeker WQ, Escobar LA, Lu CJ (1998) Accelerated degradation tests: modeling and analysis. Technometrics 40(2):89–99
Nadarajah S, Bakouch HS, Tahmasbi R (2011) A generalized Lindley distribution. Sankhya 73(20):331–359
Nassr SG, Elharoun NM (2019) Inference for exponentiated Weibull distribution under constant stress partially accelerated life tests with multiple censored. Commun Stat Appl Methods 26(2):131–148
Nelson W (1990) Accelerated testing: statistical models, test plans and data analysis. Wiley, New York
Rahman A, Sindhu TN, Lone SA, Kamal M (2020) Statistical inference for Burr type X distribution using geometric process in accelerated life testing design for time censored data. Pak J Stat Oper Res 16(3):577–586
Rahman A, Kamal M, Khan S, Khan MF, Mustafa MSA, Hussam E, Atchadé MM, Al Mutairi A (2023) Statistical inferences under step stress partially accelerated life testing based on multiple censoring approaches using simulated and real-life engineering data. Sci Rep 13(1):12452
Saxena S, Zarrin S, Kamal M, Islam AU (2012) Optimum step stress accelerated life testing for Rayleigh distribution. Int J Stat Appl 2(6):120–125
Shanker R, Sharma S, Shanker R (2013) A two-parameter lindley distribution for modeling waiting and survival times data. Appl Math 4(2):363–368
Shi X, Shi Y (2016) Constant-stress partially accelerated life tests on masked series systems under progressive type-II censoring. J Phys Sci 21:29–36
Tobias PA, Trindade DC (1995) Applied reliability, 2nd edn. Chapman and Hall/CRC
Valiollahi R, Raqab MZ, Asgharzadeh A, Alqallaf FA (2018) Estimation and prediction for power Lindley distribution under progressively type II right censored samples. Math Comput Simul 149:32–47
Xiaolin SHI, Pu LU, Yimin SHI (2018) Inference and optimal design on step-stress partially accelerated life test for hybrid system with masked data. J Syst Eng Electron 29(5):1089–1100
Zarrin S, Kamal M, Saxena S (2012) Estimation in constant stress partially accelerated life tests for Rayleigh distribution using type-I censoring. Reliab Theory Appl 7(4):41–52
Zheng D, Fang X (2017) Exact confidence limits for the acceleration factor under constant-stress partially accelerated life tests with type-I censoring. IEEE Trans Reliab 67(1):92–104
Funding
No funds, grants, or other support was received.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Confict of interest
The authors declare that they have no confict of interest.
Human or animals rights
This work does not involve human participants and/or animals.
Informed consent
Research does not involve humans.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Alam, I., Kamal, M., Rahman, A. et al. Statistical analysis using multiple censoring scheme under partially accelerated life tests for the power Lindley distribution. Int J Syst Assur Eng Manag 15, 3424–3436 (2024). https://doi.org/10.1007/s13198-024-02350-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13198-024-02350-7