Abstract
This paper investigates the time-inconsistency problem of labor taxes in an economy with balanced-budget policies and no capital taxes. With full commitment, we show that Ramsey labor taxes change with the cost of distortionary taxation and with the cost of not being able to tax capital. We numerically show that these make labor taxes increasing over time. With limited commitment, we find that this time-inconsistency problem leads to underprovision of public consumption. For our baseline parameter values, we find that imposing carefully chosen bounds on labor taxes as constitutional constraints can be optimal. While our proposed bounds sustain the Ramsey as the best sustainable equilibrium, our lower bounds alone or, in combination with some upper bounds, induce higher public consumption and higher welfare in the worst sustainable equilibrium.




Similar content being viewed by others
Notes
The finding that optimal labor taxes are increasing over time when capital cannot be taxed is connected to the comments of Atkenson et al. [3]. They observe that a positive tax on capital is comparable to an increasing tax rate on consumption and the latter corresponds to an increasing tax rate on labor income. These policies are comparable but not equivalent. In our economy, we do not count with consumption taxes and not having capital taxes eliminates an instrument that is necessary for decentralization and therefore changes the Ramsey problem.
More precisely, in Ramsey problems with full commitment, access to bonds, capital taxes, and with homothetic preferences, optimal labor taxes are typically low (even negative) in the initial period and then positive and roughly constant from then on. In contrast, in our paper, labor taxes are increasing over the transitional phase.
An alternative approach is to consider Markov-perfect equilibria as in [15].
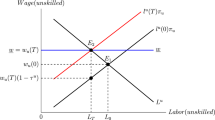
In this model, with only one source of government income, the non-negativity of public consumption requires a non-negative labor tax. Moreover, Laffer curve effects generate a ’natural’ upper bound on labor tax rates.
The first-order conditions in period 0 are different due to the initial wealth.
As usual, an optimal interior solution is assumed to exist.
We discretize the state space with \(400\) equally spaced points for \(k\in [0.01,1.5]\), \(400\) points for \(m\), and \(100\) points for \(\tau \in [0,0.9]\). We use linear interpolation for values falling outside of the grid. We ran our C++ MPI code using an IBM iDataPlex cluster, with 50 Intel Sandy Bridge 2.6 GHZ processors.
References
Abreu D, Pearce D, Stacchetti E (1990) Toward a theory of discounted repeated games with imperfect monotoring. Econometrica 58:1041–1063
Albanesi S, Armenter R (2012) Intertemporal distortions in the second best. Rev Econ Stud 79:1271–1307
Atkenson A, Chari VV, Kehoe PJ (1999) Taxing capital income: a bad idea. Fed Reserve Bank Minneap Q Rev 23:3–18
Chari VV, Christiano LJ, Kehoe PJ (1994) Optimal fiscal policy in a business cycle model. J Polit Econ 102:617–652
Chari VV, Kehoe PJ (1998) Optimal fiscal and monetary policy. Federal Reserve Bank of Minneapolis Staff, Report 251
Chari VV, Kehoe PJ (1990) Sustainable plans. J Polit Econ 98:783–802
Correia IH (1996) Should capital income be taxed in the steady state? J Public Econ 60:147–151
Domínguez B (2007) Public debt and optimal capital taxes without commitment. J Econ Theory 135:159–170
Domínguez B (2010) The time-consistency of government debt and institutional restrictions on the level of debt (manuscript submitted for publication)
Domínguez B, Feng Z (2014) An evaluation of constitutional constraints on capital taxation (manuscript submitted for publication)
Feng Z (2014) Time consistent optimal fiscal policy over the business cycle. Quant Econ (forthcoming)
Feng Z, Miao J, Peralta-Alva A, Santos M (2014) Numerical simulation of nonoptimal dynamic equilibrium models. Int Econ Rev 55:83–110
Fernández-Villaverde J, Tsyvinski A (2002) Optimal fiscal policy in a business cycle model without commitment (manuscript submitted for publication)
Judd K, Yeltekin S, Conklin J (2003) Computing supergame equilibria. Econometrica 71:1239–1254
Klein P, Krusell P, Ríos-Rull J-V (2008) Time-consistent public policy. Rev Econ Stud 75:789–808
Kydland FE, Prescott EC (1977) Rules rather than discretion: the inconsistency of optimal plans. J Polit Econ 85:473–491
Lucas RE (1990) Supply-side economics: an analytical review. Oxf Econ Pap 42:293–316
Lucas RE, Stokey NL (1983) Optimal fiscal and monetary policy in an economy without capital. J Monet Econ 12:55–93
McCallum BT (1995) Two fallacies concerning central-bank independence. Am Econ Rev 85:207–211
Mankiw NG, Weinzierl M, Yagan D (2009) Optimal taxation in theory and practice. J Econ Perspect 23:147–174
Phelan C, Stacchetti E (2001) Sequential equilibria in a Ramsey tax model. Econometrica 69:1491–1518
Rogoff K (1985) The optimal degree of commitment to an intermediate monetary target. Q J Econ 100:1169–1189
Rogoff K (1987) Reputational constraints on monetary policy. Carnegie–Rochester Conf Ser Public Policy 26:141–182
Sleet C (1997) Recursive methods for solving credible government policy problems. Mimeo, KSM-MEDS, Northwestern University, Chicago
Sleet C, Yeltekin S (2015) On the computation of value correspondences for dynamic games. Dyn Games Appl. doi:10.1007/s13235-015-0139-1
Stockman D (2001) Balanced-budget rules: welfare loss and optimal policies. Rev Econ Dyn 4:438–459
Author information
Authors and Affiliations
Corresponding author
Additional information
We thank the Editors and an anonymous Referee for their valuable comments. All the remaining errors are ours.
Appendix
Appendix
1.1 Calibration
In order to calibrate the parameters for our quantitative exercise, we consider an initial steady state that corresponds to an economy with similar statistics to those of the USA. In our simulations, one period corresponds to 1 year.
Our calibration follows that of [4], which is consistent with US data. In the initial steady state, the tax rates on capital and labor income are set equal to 27.1 and 23.7 %, respectively. We choose a public consumption to output ratio equal to 19 % and consider no public debt.
We assume the utility function (2) and a Cobb-Douglas production function \(y_{t}=k_{t}^{\alpha }n_{t}^{1-\alpha }.\) We choose a capital share of 0.34 and a depreciation rate of 0.08. The discount factor is set to deliver a capital to output ratio of 2.71 in the initial steady state. In (2), the coefficient of risk aversion \(\sigma \) is set equal to unity and the labor-supply elasticity is set so that \(\chi \)= 0.32. The weight on labor disutility \(\gamma _{n}\) is chosen so that hours worked are 0.23 in the initial steady state. The weight on public consumption \(\gamma _{g}\) is chosen so that social planner’s solution delivers a public consumption to output ratio equal to 19 %.
Table 1 summarizes the parameter values used in our baseline economy.
Rights and permissions
About this article
Cite this article
Domínguez, B., Feng, Z. The Time-Inconsistency Problem of Labor Taxes and Constitutional Constraints. Dyn Games Appl 6, 225–242 (2016). https://doi.org/10.1007/s13235-015-0149-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13235-015-0149-z