Dynamic Price Competition with Switching Costs

Abstract

We characterize a relatively simple Markov Perfect equilibrium in a continuous-time dynamic model of competition with switching costs. When firms cannot price-discriminate between old and new consumers, the effect of switching costs on prices critically depends on the degree of market share asymmetries: If firms’ market shares are sufficiently asymmetric, an increase in switching costs leads to higher prices. However, as market shares become sufficiently symmetric, price competition turns fiercer, and in the long-run, switching costs have a pro-competitive effect. If firms can price-discriminate, an increase in switching costs make all consumers better off regardless of market structure.

Appendices

Appendix 1: Forward-Looking Consumers

In this appendix, we show that the pro-competitive effect of switching costs on steady-state prices found in the basic model of Sect. 2 is robust to allowing for more forward-looking consumers who aim to maximize their total discounted consumption surplus over the infinite horizon. Hence, they may abstain from switching when they correctly anticipate price increases in the future. In our extended model of switching, we assume that consumers are able to correctly anticipate infinite price trajectories when deciding whether or not to switch. However, we only consider the open-loop solution to the stochastic optimization problem in which a consumer has to decide whether or not to switch taking into account future opportunities to switch (at random times) subject to (random) switching costs. For simplicity, we only focus on the case of (exogenously given) symmetric switching costs.

Let us denote by $p_{i}^{e}(\tau )$ consumers’ anticipation of firm i’s price at time $\tau >t$. Given current prices, $p_{i}(t)$, consumers assume

$$\begin{aligned} p_{1}^{e}(\tau )= & {} \alpha p_{1}(t)\hbox {e}^{-\gamma (\tau -t)}+\beta \end{aligned}$$

(9)

$$\begin{aligned} p_{2}^{e}(\tau )= & {} \alpha p_{2}(t)\hbox {e}^{-\gamma (\tau -t)}+\beta , \end{aligned}$$

(10)

where $\alpha ,\beta ,\gamma >0$. Note that consumers anticipate that price differences will gradually decrease over time. We assume all consumers use a normalized discount rate.

When an opportunity to switch arises at time $t>0$ , a consumer currently served by firm j would opt for firm i provided that

$$\begin{aligned}&{\textstyle \int \limits _{t}^{\infty }}(v-p_{i}^{e}(\tau ))\hbox {e}^{-\tau }\hbox {d}\tau -\tilde{s} >{\textstyle \int \limits _{t}^{\infty }}(v-p_{j}^{e}(\tau ))\hbox {e}^{-\tau }\hbox {d}\tau . \end{aligned}$$

Thus, the probability $\bar{q}_{ji}(t)$ that a customer served by firm j switches to firm i at time $t>0$ is given by

$$\begin{aligned} \bar{q}_{ji}(t)=\Pr \left( {\textstyle \int \limits _{t}^{\infty }}(v-p_{i}^{e}(\tau ))\hbox {e}^{-\tau }\hbox {d}\tau -\tilde{s}>{\textstyle \int \limits _{t}^{\infty }}(v-p_{j}^{e}(\tau ))\hbox {e}^{-\tau }\hbox {d}\tau \right) \cdot \end{aligned}$$

With some algebra,

$$\begin{aligned} \bar{q}_{ji}(t)=\frac{1}{2}(1-s)-\frac{\alpha }{1+\gamma }\left( p_{i}(t)-p_{j}(t)\right) , \end{aligned}$$

assuming that $p_{i}(t)-p_{j}(t)\in \left[ -\frac{1+\gamma }{\alpha }(1-s), \frac{1+\gamma }{\alpha }(1+s)\right]$. Conversely, the probability that a customer already served by firm i maintains this relationship at time $t>0$ is given by

$$\begin{aligned} \bar{q}_{ii}(t)= & {} \Pr \left( \tilde{s}>{\textstyle \int \limits _{t}^{\infty }}(p_{i}^{e}(\tau )-p_{j}^{e}(\tau ))\hbox {e}^{-(\tau -t)}\hbox {d}\tau \right) \\= & {} \frac{1}{2}(1+s)-\frac{\alpha }{1+\gamma }\left( p_{i}(t)-p_{j}(t)\right) . \end{aligned}$$

Note that when $\frac{\alpha }{1+\gamma }<1,$ forward-looking consumers are less sensitive to current price differences than myopic consumers.

By comparing switching probabilities with myopic and with forward-looking consumers, it can be seen that equilibrium prices $\bar{p}_{i}(x_{1})$ in the latter case can be obtained by a simple rescaling of the equilibrium prices in the former, i.e., $\bar{p}_{i}(x_{1})=\frac{1+\gamma }{\alpha } p_{i}(x_{1})\cdot$ Therefore, the price dynamics with forward-looking consumers remained unaltered as compared to the myopic consumers case. In other words, the pro-competitive effect of switching costs on steady- state prices survives the presence of more sophisticated consumers. Still, the pro-competitive effect is slightly attenuated because forward-looking consumers are less sensitive to current price differences.

For completeness, let us stress that consumers’ anticipation of price differences over time is correct provided that

$$\begin{aligned} p_{1}^{e}(t)-p_{2}^{e}(t)=\frac{1+\gamma }{\alpha }\left( p_{1}(t)-p_{2}(t)\right) , \end{aligned}$$

or equivalently, using expressions (9), (10) and Proposition 1,

$$\begin{aligned} \alpha \hbox {e}^{-\gamma t}=\frac{1+\gamma }{\alpha }\frac{2}{3}\left( s-a\right) x_{1}(0)\hbox {e}^{-\left( 1-\frac{s+2a}{3}\right) t}\cdot \end{aligned}$$

For this to be the case, $\alpha$ and must take the following values,

$$\begin{aligned} \begin{array}{ccc} \gamma =1-\frac{s+2a}{3}&\quad \text {and}&\quad \alpha =\sqrt{2\left( 1-\frac{s+2a}{3 }\right) (\frac{s-a}{3})x_{1}(0)}. \end{array} \end{aligned}$$

Appendix 2: Proofs of Lemmas and Propositions

Basic Model

1.1 Proof of Proposition 1

The Hamiltonians are

$$\begin{aligned} \mathcal {H}_{i}=\hbox {e}^{-\rho t}[\pi _{i}+\lambda _{i}\dot{x}_{1}], \end{aligned}$$

for $i=1,2$. The Hamiltonians are strictly concave so that first order conditions for MPE are also sufficient (see [5]),

$$\begin{aligned}&\frac{\partial \mathcal {H}_{i}}{\partial p_{i}}=0\\&-\,\frac{\partial \mathcal {H}_{i}}{\partial x_{1}}-\frac{\partial \mathcal {H} _{i}}{\partial p_{j}}\frac{\partial p_{j}}{\partial x_{1}}=\dot{\lambda } _{i}-\rho \lambda _{i}, \end{aligned}$$

for $i=1,2$. These, respectively, lead to:

$$\begin{aligned}&p_{1}=\frac{1}{2}\left( p_{2}+s\left( x_{1}-\frac{1}{2}\right) +\frac{1}{2} -\lambda _{1}\right) \end{aligned}$$

(11)

$$\begin{aligned}&-\,sp_{1}+(1-s)\lambda _{1}-(p_{1}+\lambda _{1})\frac{\partial p_{2}}{\partial x_{1}}=\dot{\lambda }_{1}-\rho \lambda _{1} \end{aligned}$$

(12)

$$\begin{aligned}&p_{2}=\frac{1}{2}\left( p_{1}-s\left( x_{1}-\frac{1}{2}\right) +\frac{1}{2} +\lambda _{2}\right) \end{aligned}$$

(13)

$$\begin{aligned}&sp_{2}+(1-s)\lambda _{2}-(p_{2}-\lambda _{2})\frac{\partial p_{1}}{\partial x_{1}}=\dot{\lambda }_{2}-\rho \lambda _{2} \end{aligned}$$

(14)

Equations (11) and (13) are firms’ best reply functions. Using them we can obtain equilibrium prices,

$$\begin{aligned} p_{1}= & {} \frac{s}{3}\left( x_{1}-\frac{1}{2}\right) +\frac{1}{2}+\frac{1}{3} (\lambda _{2}-2\lambda _{1}) \\ p_{2}= & {} -\frac{s}{3}\left( x_{1}-\frac{1}{2}\right) +\frac{1}{2}+\frac{1}{3} (2\lambda _{2}-\lambda _{1}) \end{aligned}$$

Thus,

$$\begin{aligned} \begin{array}{cccc} \frac{\partial p_{2}}{\partial x_{1}}=-\frac{s}{3}&\,&\frac{\partial p_{1} }{\partial x_{1}}=\frac{s}{3}&\end{array} \end{aligned}$$

Substituting into (12) and (14) we obtain

$$\begin{aligned} \frac{2s}{3}p_{2}+\left( 1-\frac{2s}{3}\right) \lambda _{2}= & {} \dot{\lambda }_{2}-\rho \lambda _{2} \\ -\frac{2s}{3}p_{1}+\left( 1-\frac{2s}{3}\right) \lambda _{1}= & {} \dot{\lambda }_{1}-\rho \lambda _{1} \end{aligned}$$

We solve this system of differential equations by the method of undetermined coefficients. Assume $\lambda _{i}=a_{i}(x_{1}-\frac{1}{2})+b_{i}$ for $i=1,2$. Substitution into the last equation yields

$$\begin{aligned}&-\frac{2s}{3}\left( \frac{s}{3}\left( x_{1}-\frac{1}{2}\right) +\frac{1}{2}+\frac{1}{3} \left( a_{2}(x_{1}-\frac{1}{2}\right) +b_{2}-2a_{1}\left( x_{1}-\frac{1}{2}\right) -2b_{1})\right) \\&\qquad +\left( 1- \frac{2s}{3}\right) \left( a_{1}\left( x_{1}-\frac{1}{2}\right) +b_{1}\right) =a_{1}\dot{x}_{1}-\rho \left( a_{1}\left( x_{1}-\frac{1}{2}\right) +b_{1}\right) \\&\quad =a_{1}\left( -x_{1}(1-s)+\frac{1-s}{2}-p_{1}+p_{2}\right) -\rho a_{1}\left( x_{1}- \frac{1}{2}\right) -\rho b_{1} \\&\quad = a_{1}\left( -x_{1}(1-s)+\frac{1-s}{2}-\frac{2s}{3}(x_{1}-\frac{1}{2})+\frac{ \lambda _{1}+\lambda _{2}}{3}\right) -\rho a_{1}\left( x_{1}-\frac{1}{2}\right) -\rho b_{1} \\&\quad = a_{1}\left( -(1-s)\left( x_{1}-\frac{1}{2}\right) -\frac{2s}{3}\left( x_{1}-\frac{1}{2}\right) +\frac{ a_{1}\left( x_{1}-\frac{1}{2}\right) +b_{1}+a_{2}\left( x_{1}-\frac{1}{2}\right) +b_{2}}{3}\right) \\&\qquad -\,\rho a_{1}\left( x_{1}-\frac{1}{2}\right) -\rho b_{1} \end{aligned}$$

This results in the following two equations:

$$\begin{aligned}&-\frac{2}{9}s^{2}+\frac{2}{9}s(2a_{1}-a_{2})+\left( 1-\frac{2s}{3}\right) a_{1}=-\left( 1-\frac{ s}{3}\right) a_{1}+\frac{1}{3}(a_{1}+a_{2})a_{1}-\rho a_{1} \end{aligned}$$

(15)

$$\begin{aligned}&-\frac{s}{3}-\frac{2s}{9}(b_{2}-2b_{1})+b_{1}\left( 1-\frac{2s}{3}\right) =\frac{1}{3} (b_{1}+b_{2})a_{1}+\frac{a_{1}}{2}\left( 1-\frac{s}{3}\right) -\rho b_{1} \end{aligned}$$

(16)

In a similar fashion,

$$\begin{aligned}&\frac{2s}{3}\left( -\frac{s}{3}\left( x_{1}-\frac{1}{2}\right) +\frac{1}{2}+ \frac{1}{3}(2a_{2}\left( x_{1}-\frac{1}{2}\right) +2b_{2}-a_{1}\left( x_{1}- \frac{1}{2}\right) -b_{1})\right) \\&\qquad +\,(1-\frac{2s}{3})(a_{2}\left( x_{1}-\frac{1 }{2}\right) +b_{2}) \\&\quad = a_{2}\dot{x}_{1}-\rho (a_{2}\left( x_{1}-\frac{1}{2}\right) +b_{2}) \\&\quad = a_{2}\left( -x_{1}(1-s)+\frac{1-s}{2}-\frac{2s}{3}\left( x_{1}-\frac{1}{2}\right) +\frac{ a_{1}\left( x_{1}-\frac{1}{2}\right) +b_{1}+a_{2}\left( x_{1}-\frac{1}{2} \right) +b_{2}}{3}\right) \\&\qquad -\,\rho a_{2}\left( x_{1}-\frac{1}{2}\right) -\rho b_{2} \\&\quad = a_{2}\left( -(1-s)\left( x_{1}-\frac{1}{2}\right) -\frac{2s}{3}(x_{1}-\frac{1}{2})+\frac{ a_{1}\left( x_{1}-\frac{1}{2}\right) +b_{1}+a_{2}\left( x_{1}-\frac{1}{2} \right) +b_{2}}{3}\right) \\&\qquad -\,\rho a_{2}\left( x_{1}-\frac{1}{2}\right) -\rho b_{2} \end{aligned}$$

We obtain two additional equations:

$$\begin{aligned}&-\frac{2}{9}s^{2}+\frac{2}{9}s(2a_{2}-a_{1})+\left( 1-\frac{2s}{3}\right) a_{2}=-\left( 1-\frac{ s}{3}\right) a_{2}+\frac{1}{3}(a_{1}+a_{2})a_{2}-\rho a_{2}\end{aligned}$$

(17)

$$\begin{aligned}&\frac{s}{3}+\frac{2s}{9}(2b_{2}-b_{1})+b_{2}\left( 1-\frac{2s}{3}\right) =\frac{1}{3} (b_{1}+b_{2})a_{2}+\frac{a_{2}}{2}\left( 1-\frac{s}{3}\right) -\rho b_{2} \end{aligned}$$

(18)

Thus, substracting (15) from (17) we get:

$$\begin{aligned} \left[ 1-\frac{s}{3}-\frac{1}{3}(a_{1}+a_{2})+\frac{2}{9}s+1-\frac{2s}{3} +\rho \right] (a_{1}-a_{2})=0 \end{aligned}$$

Hence, $a_{1}-a_{2}=0$. Let $a_{1}=a_{2}=a,$ we solve the quadratic equation implicit in (15):

$$\begin{aligned} 2a^{2}-3\left( 2+\rho -\frac{7}{9}s\right) a+\frac{2}{3}s^{2}=0 \end{aligned}$$

Then (16) and (18) imply $b_{1}+b_{2}=0$ and

$$\begin{aligned} b_{1}=\frac{s(1+\frac{a}{2})}{3(1+\rho )}-\frac{a}{2(1+\rho )} \end{aligned}$$

So the equilibrium strategies can be rewritten as

$$\begin{aligned} p_{1}= & {} \frac{s}{3}\left( x_{1}-\frac{1}{2}\right) +\frac{1}{2}+\frac{1}{3} (\lambda _{2}-2\lambda _{1}) \\ p_{2}= & {} -\frac{s}{3}\left( x_{1}-\frac{1}{2}\right) +\frac{1}{2}+\frac{1}{3} (2\lambda _{2}-\lambda _{1}) \end{aligned}$$

Or equivalently,

$$\begin{aligned} p_{1}= & {} \frac{s-a}{3}\left( x_{1}-\frac{1}{2}\right) +\frac{1}{2}+\frac{a}{ 2(1+\rho )}-\frac{s(1+\frac{a}{2})}{3(1+\rho )} \\ p_{2}= & {} -\frac{s-a}{3}\left( x_{1}-\frac{1}{2}\right) +\frac{1}{2}+\frac{a}{ 2(1+\rho )}-\frac{s(1+\frac{a}{2})}{3(1+\rho )} \end{aligned}$$

Finally, we note that given the assumption $s<\frac{3}{5}$ the pricing policies satisfy:

$$\begin{aligned} p_{1}(x_{1})-p_{2}(x_{1})=\frac{2}{3}(s-a)\left( x_{1}-\frac{1}{2}\right) \in \left( -\frac{1-s}{2},\frac{1-s}{2}\right) \end{aligned}$$

so that $q_{0},q_{1}\in (0,1)$.

1.2 Proof of Lemma 3

We first note that implicit differentiation in (3) yields:

$$\begin{aligned} \frac{\partial a}{\partial s}=\frac{4s+7a}{9(2+\rho )-7s-12a}\in (0,1) \end{aligned}$$

• (i) Using this result, it is straightforward to see that $\frac{\partial p_{2}}{\partial s}<0.$ Taking derivatives,

  $$\begin{aligned} \frac{\partial p_{2}}{\partial s}= & {} -\frac{1}{3}\left( \left( 1-\frac{ \partial a}{\partial s}\right) \left( x_{1}-\frac{1}{2}\right) +\frac{ \partial a}{\partial s}\right) \\&-\,\frac{1}{3}\frac{1}{1+\rho }\left( \frac{2}{3}\left( \frac{s}{3}+\frac{a}{ 2}\right) +\left( 1-\frac{s}{3}\right) \left( \frac{1}{3}+\frac{1}{2}\frac{ \partial a}{\partial s}\right) \right) \end{aligned}$$

• (ii) Taking derivatives,

  $$\begin{aligned} \frac{\partial p_{1}}{\partial s}= & {} \frac{1}{3}\left( \left( 1-\frac{ \partial a}{\partial s}\right) x_{1}-\frac{1}{2}\left( 1+\frac{\partial a}{ \partial s}\right) \right) \\&-\frac{1}{3}\frac{1}{1+\rho }\left( \frac{2}{3}\left( \frac{s}{3}+\frac{a}{ 2}\right) +\left( 1-\frac{s}{3}\right) \left( \frac{1}{3}+\frac{1}{2}\frac{ \partial a}{\partial s}\right) \right) \end{aligned}$$

  The second term is negative, while the sign of the first term cannot be determined in general. Solving for $x_{1}$, expression above is positive if and only if

  $$\begin{aligned} x_{1}>\widehat{x}_{1}\!=\!\frac{1}{\left( 1\!-\!\frac{\partial a}{\partial s}\right) }\left( \frac{1}{1\!+\!\rho }\left( \frac{2}{3}\left( \frac{s}{3}\!+\!\frac{a}{2} \right) +\left( 1-\frac{s}{3}\right) \left( \frac{1}{3}+\frac{1}{2}\frac{ \partial a}{\partial s}\right) \right) +\frac{1}{2} \left( 1+\frac{\partial a }{\partial s}\right) \right) \end{aligned}$$

  The fact that $\widehat{x}_{1}>\frac{1}{2}$ follows since $\frac{\partial p_{1}}{\partial s}$ is weakly increasing in $x_{1}\$and $\frac{\partial p_{1}}{\partial s}<0$ for $x_{1}=\frac{1}{2},$ as the first term becomes $- \frac{\partial a}{\partial s}<0.$

• (iii) It follows from the fact that the price differential $p_{1}-p_{2}$ is directly proportional to $s-a$ and, as shown above, $\frac{\partial a}{ \partial s}<1.$

• (iv) The proof is provided in the main text.

1.3 Proof of Lemma 4

(i) It follows from the fact that $\dot{p}(t)$ is inversely proportional to $s-a$ and, as shown above, $\frac{\partial a}{\partial s}<1.$ (ii) The transition to the steady state occurs at a rate which is inversely proportional to $\frac{s+2a}{3},$ and as shown above, $\frac{\partial a}{ \partial s}>0.$

1.4 Proof of Lemma 5

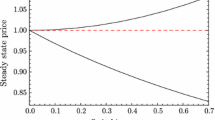
Steady-state prices are

$$\begin{aligned} \lim _{t\rightarrow \infty }p_{i}(t)=p^{*}=\frac{1}{2}+\frac{a}{2(1+\rho ) }-\frac{s(1+\frac{a}{2})}{3(1+\rho )}. \end{aligned}$$

Taking derivatives w.r.t. s, 

$$\begin{aligned} \frac{\partial p^{*}}{\partial s}=\frac{a}{2(1+\rho )}\frac{\partial a}{ \partial s}-\frac{1+\frac{a}{2}}{3(1+\rho )}-\frac{s}{6(1+\rho )}\frac{ \partial a}{\partial s}<0, \end{aligned}$$

where the inequality follows from $\frac{\partial a}{\partial s}\in (0,1)$ and $a<\frac{s}{2}$.

Price Discrimination

1.1 Proof of Proposition 2

The Hamiltonians are:

$$\begin{aligned} \mathcal {H}_{i}=\hbox {e}^{-\rho t}[\pi _{i}+\lambda _{i}\dot{x}_{1}] \end{aligned}$$

for $i=1,2.$ A necessary condition for optimality is:

$$\begin{aligned} \frac{\partial \pi _{i}}{\partial p_{ii}}=-\lambda _{i}\frac{\partial \dot{x} _{1}}{\partial p_{ii}} \frac{\partial \pi _{i}}{\partial p_{ji}} =-\lambda _{i}\frac{\partial \dot{x}_{1}}{\partial p_{ji}} \end{aligned}$$

These conditions imply:

$$\begin{aligned} \frac{1+s}{2}-2p_{11}+p_{12}-\lambda _{1}= & {} 0 \\ \frac{1-s}{2}-2p_{12}+p_{11}+\lambda _{2}= & {} 0 \\ \frac{1-s}{2}-2p_{21}+p_{22}-\lambda _{1}= & {} 0 \\ \frac{1+s}{2}-2p_{22}+p_{21}+\lambda _{2}= & {} 0 \end{aligned}$$

Note that these “instantaneous” best reply functions do not depend on $x_{1}$. Hence,

$$\begin{aligned} \begin{array}{c} p_{11}=p_{22}=\frac{1}{2}\left( 1+\frac{s}{3}\right) +\frac{\lambda _{2}-2\lambda _{1}}{3} \\ p_{12}=p_{21}=\frac{1}{2}\left( 1-\frac{s}{3}\right) +\frac{2\lambda _{2}-\lambda _{1}}{3} \end{array} \end{aligned}$$

The remaining conditions are:

$$\begin{aligned} -\frac{\partial \mathcal {H}_{i}}{\partial x_{1}}-\frac{\partial \mathcal {H} _{i}}{\partial p_{ij}}\frac{\partial p_{ij}}{\partial x_{1}}-\frac{\partial \mathcal {H}_{i}}{\partial p_{jj}}\frac{\partial p_{jj}}{\partial x_{1}}=\dot{ \lambda }_{i}-\rho \lambda _{i}\cdot \end{aligned}$$

Since $\frac{\partial p_{ii}}{\partial x_{1}}=\frac{\partial p_{ij}}{ \partial x_{1}}=0$ we have

$$\begin{aligned}&-p_{11}\left( \frac{1+s}{2}-p_{11}+p_{12}\right) +p_{21}\left( \frac{1-s}{2}-p_{21}+p_{22}\right) \\&+\,\lambda _{1}(1-s+p_{11}-p_{12}-p_{21}+p_{22})=\dot{\lambda }_{1}-\rho \lambda _{1} \end{aligned}$$

and

$$\begin{aligned}&-p_{12}\left( \frac{1-s}{2}-p_{12}+p_{11}\right) +p_{22}\left( \frac{1}{2} (1+s)-p_{22}+p_{21}\right) \\&+\,\lambda _{2}(1-s+p_{11}-p_{12}-p_{21}+p_{22})= \dot{\lambda }_{2}-\rho \lambda _{2} \end{aligned}$$

We posit a solution of the form $\lambda _{i}=b_{i},$ $i=1,2.$ Solving the equations above, we respectively get:

$$\begin{aligned}&-\left( \frac{1}{2}+\frac{s}{6}+\frac{b_{2}-2b_{1}}{3}\right) \left( \frac{ 1}{2}+\frac{s}{6}+\frac{b_{2}+b_{1}}{3}\right) \\&\quad +\,\left( \frac{1}{2}-\frac{s}{6}+\frac{2b_{2}-b_{1}}{3}\right) \left( \frac{ 1}{2}-\frac{s}{6}+\frac{b_{2}+b_{1}}{3}\right) +b_{1}\left( 1-\frac{s}{3} \right) \\&\quad =-b_{1}\rho \\&\quad -\,\left( \frac{1}{2}-\frac{s}{6}+\frac{2b_{2}-b_{1}}{3}\right) \left( \frac{ 1}{2}-\frac{s}{6}+\frac{b_{2}+b_{1}}{3}\right) \\&\quad +\,\left( \frac{1}{2}+\frac{s}{6}+\frac{b_{2}-2b_{1}}{3}\right) \left( \frac{ 1}{2}+\frac{s}{6}+\frac{b_{2}+b_{1}}{3}\right) +b_{2}\left( 1-\frac{s}{3} \right) \\&\quad =-b_{2}\rho \end{aligned}$$

Adding these equations we obtain:

$$\begin{aligned} \left( b_{1}+b_{2}\right) \left( 1+\rho -\frac{s}{3}\right) =0. \end{aligned}$$

Thus, $b_{1}=-b_{2}$. Plugging this into the FOCs above,

$$\begin{aligned} b_{1}=\frac{\frac{s}{3}}{1+\rho -\frac{2s}{3}}\cdot \end{aligned}$$

Thus, prices are

$$\begin{aligned} p_{11}= & {} p_{22}=\frac{1}{2}-\frac{s}{3}\left( \frac{1}{1+\rho -\frac{2s}{3}} -\frac{1}{2}\right) \\ p_{12}= & {} p_{21}=\frac{1}{2}-\frac{s}{3}\left( \frac{1}{1+\rho -\frac{2s}{3}} +\frac{1}{2}\right) . \end{aligned}$$

Note that the price discount to new consumers is:

$$\begin{aligned} p_{ii}-p_{ij}=\frac{s}{3}\cdot \end{aligned}$$

Condition $s<1$ guarantees that $p_{ii}-p_{ij}\in \left[ -\frac{1}{2}(1-s), \frac{1}{2}(1+s)\right]$ and $p_{ji}-p_{jj}\in \left[ -\frac{1}{2}(1+s), \frac{1}{2}(1-s)\right]$, as we had previously assumed.

1.2 Proof of Lemma 6

The comparative statics of prices with respect to s is,

$$\begin{aligned} \frac{\partial p_{ij}}{\partial s}= & {} -3\frac{1+\rho }{\left( 2s-3\rho -3\right) ^{2}}-\frac{1}{6}<0 \\ \frac{\partial p_{ii}}{\partial s}= & {} \frac{\partial p_{ij}}{\partial s}+ \frac{1}{3} \\= & {} -3\frac{1+\rho }{\left( 2s-3\rho -3\right) ^{2}}+\frac{1}{6}<0 \end{aligned}$$

under the assumption $\rho <1.$

Asymmetric Switching Costs

1.1 Proof of Proposition 3

As in the proof of Proposition 1, the Hamiltonians are

$$\begin{aligned} \mathcal {H}_{i}=\hbox {e}^{-\rho t}[\pi _{i}+\lambda _{i}\dot{x}_{1}] \end{aligned}$$

for $i=1,2$. First order conditions (which in this case due to concavity are also sufficient) are:

$$\begin{aligned}&\frac{\partial \mathcal {H}_{i}}{\partial p_{i}}=0\\&-\frac{\partial \mathcal {H}_{i}}{\partial x_{1}}-\frac{\partial \mathcal {H} _{i}}{\partial p_{j}}\frac{\partial p_{j}}{\partial x_{1}}=\dot{\lambda } _{i}-\rho \lambda _{i} \end{aligned}$$

The first order conditions lead to:

$$\begin{aligned}&p_{1}=\frac{1}{2}\left( p_{2}+\frac{s}{2}x_{1}+\frac{1}{2}-\lambda _{1}\right) \end{aligned}$$

(19)

$$\begin{aligned}&-\frac{s}{2}p_{1}+\left( 1-\frac{s}{2}\right) \lambda _{1}-(p_{1}+\lambda _{1})\frac{ \partial p_{2}}{\partial x_{1}}=\dot{\lambda }_{1}-\rho \lambda _{1} \end{aligned}$$

(20)

$$\begin{aligned}&p_{2}=\frac{1}{2}\left( p_{1}-\frac{s}{2}x_{1}+\frac{1}{2}+\lambda _{2}\right) \end{aligned}$$

(21)

$$\begin{aligned}&\frac{s}{2}p_{2}+(1-\frac{s}{2})\lambda _{2}-(p_{2}-\lambda _{2})\frac{\partial p_{1}}{\partial x_{1}}=\dot{\lambda }_{2}-\rho \lambda _{2} \end{aligned}$$

(22)

Here, (19) and (21) imply that equilibrium prices are of the form:

$$\begin{aligned} p_{1}= & {} \frac{s}{6}x_{1}+\frac{1}{2}+\frac{\lambda _{2}-2\lambda _{1}}{3} \\ p_{2}= & {} -\frac{s}{6}x_{1}+\frac{1}{2}+\frac{2\lambda _{2}-\lambda _{1}}{3} \end{aligned}$$

Hence $\frac{\partial p_{1}}{\partial x_{1}}=-\frac{\partial p_{2}}{\partial x_{1}}=\frac{s}{6}$. Substituting into (20) and (22) we obtain

$$\begin{aligned} \frac{s}{3}p_{2}+\left( 1-\frac{s}{3}\right) \lambda _{2}= & {} \dot{\lambda }_{2}-\rho \lambda _{2} \\ -\frac{s}{3}p_{1}+\left( 1-\frac{s}{3}\right) \lambda _{1}= & {} \dot{\lambda }_{1}-\rho \lambda _{1} \end{aligned}$$

We solve using method of undetermined coefficients. Assume $\lambda _{i}=a_{i}x_{1}+b_{i}$ for $i=1,2$. Substitution into the last equation yields

$$\begin{aligned}&-\frac{s}{3}\left( \frac{s}{6}x_{1}+\frac{1}{2}+\frac{1}{3} (a_{2}x_{1}+b_{2}-2a_{1}x_{1}-2b_{1})\right) +\left( 1-\frac{s}{3}\right) (a_{1}x_{1}+b_{1}) \\&\quad = a_{1}\dot{x}_{1}-\rho (a_{1}x_{1}+b_{1}) \\&\quad = a_{1}\left( -x_{1}\left( 1-\frac{s}{2}\right) +\frac{1}{2}-p_{1}+p_{2}\right) -\rho a_{1}x_{1}-\rho b_{1} \\&\quad = a_{1}\left( -x_{1}\left( 1-\frac{s}{2}\right) +\frac{1}{2}-\frac{1s}{3}x_{1}+\frac{ \lambda _{1}+\lambda _{2}}{3}\right) -\rho a_{1}x_{1}-\rho b_{1} \\&\quad = a_{1}\left( -x_{1}\left( 1-\frac{s}{2}+\frac{s}{3}\right) +\frac{1}{2}+\frac{ a_{1}x_{1}+b_{1}+a_{2}x_{1}+b_{2}}{3}\right) -\rho a_{1}x_{1}-\rho b_{1} \end{aligned}$$

This results in the following two equations:

$$\begin{aligned}&-\frac{s^{2}}{18}-\frac{s}{9}(a_{2}-2a_{1})+\left( 1-\frac{s}{3}\right) a_{1}=-\left( 1-\frac{s }{6}\right) a_{1}+\frac{1}{3}(a_{1}+a_{2})a_{1}-\rho a_{1} \end{aligned}$$

(23)

$$\begin{aligned}&-\frac{s}{6}-\frac{s}{9}(b_{2}-2b_{1})+b_{1}\left( 1-\frac{s}{3}\right) =\frac{1}{3} (b_{1}+b_{2})a_{1}+\frac{a_{1}}{2}-\rho b_{1} \end{aligned}$$

(24)

In a similar fashion, we obtain two additional equations:

$$\begin{aligned}&-\frac{s^{2}}{18}-\frac{s}{9}(a_{1}-2a_{2})+\left( 1-\frac{s}{3}\right) a_{2}=-\left( 1-\frac{s }{6}\right) a_{2}+\frac{1}{3}(a_{1}+a_{2})a_{2}-\rho a_{2} \end{aligned}$$

(25)

$$\begin{aligned}&\frac{s}{6}+\frac{s}{9}(2b_{2}-b_{1})+b_{2}\left( 1-\frac{s}{3}\right) =\frac{1}{3} (b_{1}+b_{2})a_{2}+\frac{a_{2}}{2}-\rho b_{2} \end{aligned}$$

(26)

The symmetry of Eqs. (23) and (25) imply $a_{1}=a_{2}=a$ which is a solution to the quadratic equation:

$$\begin{aligned} g(a)=2a^{2}-3\left( 2+\rho -\frac{7}{18}s\right) a+\frac{s^{2}}{6}=0 \end{aligned}$$

By adding and substracting (24) and (26) we obtain

$$\begin{aligned} b_{1}+b_{2}=\frac{a}{1+\rho -\frac{2}{3}\left( a+\frac{s}{3}\right) } b_{1}-b_{2}= \frac{s}{3(1+\rho )} \end{aligned}$$

It follows that

$$\begin{aligned} b_{1}= & {} \frac{1}{2}\left[ \frac{s}{3(1+\rho )}+\frac{a}{1+\rho -\frac{2}{3} \left( a+\frac{s}{3}\right) }\right] \\ b_{2}= & {} \frac{1}{2}\left[ -\frac{s}{3(1+\rho )}+\frac{a}{1+\rho -\frac{2}{3} \left( a+\frac{s}{3}\right) }\right] \end{aligned}$$

The equilibrium pricing strategies can be written as:

$$\begin{aligned} p_{1}= & {} \frac{x_{1}}{3}\left( \frac{s}{2}-a\right) +\frac{1}{2}-\frac{1}{2} \left( \frac{s}{3(1+\rho )}+\frac{a}{1+\rho -\frac{2}{3}\left( a+\frac{s}{3}\right) } \right) \\ p_{2}= & {} -\frac{x_{1}}{3}\left( \frac{s}{2}-a\right) +\frac{1}{2}-\frac{1}{2} \left( \frac{s}{3(1+\rho )}-\frac{a}{1+\rho -\frac{2}{3}\left( a+\frac{s}{3}\right) } \right) , \end{aligned}$$

which concludes the proof.