Abstract
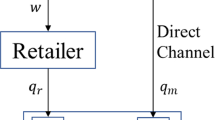
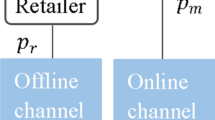
This paper investigates the dynamic pricing strategies of firms selling complementary products in a marketing channel. The problem is modelled as a non-cooperative differential game that takes place between decisions makers controlling transfer and retail prices. We computed and compared prices and sales rates of channel members under two scenarios: (i) The first involves a single retailer that sells a unique brand produced by a monopolist manufacturer and (ii) in the second, a complementary product is introduced by an additional manufacturer. We found that in both scenarios, transfer and retail prices decrease over time, but prices decrease faster when the complementary product is introduced into the market. Furthermore, the entry of the complementary product onto the market boosts the sales rate of the existing product. Finally, we found that the retailer in the second scenario always has a non-negative retail margin, meaning that practicing a loss-leadership strategy is not optimal.



Similar content being viewed by others
Notes
The interested reader could read [13] for a complete survey of non-competitive models on this topic.
See [14] for a complete survey on the topic.
See [1].
The author built a general model and then examined different subclasses of it. In the particular case where the diffusion rate was technically similar to the model used in our paper, the author found that the monopolistic firm fixed a price that decreased monotonically. This result was not affected by the discount rate level or the presence of cost learning.
Competition is attributed either to the presence of substitute products offered by competitors in an oligopoly, or to the introduction of new generations of technologies by the same firm.
The only exception is Dockner and Gaunersdorfer [8], in which the authors used a feedback information structure. But here again, the authors examined the case of a duopoly where two substitute products were sold.
A common assumption in this body of literature is that the number of adopters is equal to the number of units sold. Hence, the cumulative number of adopters at the end of the planning horizon is equal to the market potential.
We assume that both manufacturers face similar constant unit production costs c.
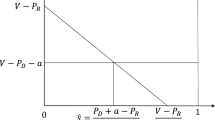
This expression represents the sales rate when \(x(t)=0\) and when the product is sold at cost.
Since the objective functionals are quadratic in the state and the control variables, and the state dynamics is linear in these variables, we have a linear-quadratic differential game.
Another result not reported here is \(\alpha _{0}=2\beta _{0}\).
If these expressions are positive.
The differential game studied under this second scenario is particular in that the Ricatti Eqs. (44)–(46) and (50)–(52) given in “Appendix B” are highly nonlinear. We solve them numerically with MATLAB’s fsolve routine to obtain the value function coefficients \(h_{11},h_{12},h_{13},h_{21},h_{22}\), \(h_{23}\) and \(R_{1},R_{2},R_{3}\), respectively. Once these coefficients are known, we compute the values function coefficients \(h_{14},h_{15},h_{24}\), \(h_{25}\) and \(R_{4},R_{5}\) from (47)–(48) and (53)–(54). Finally, we solve the Eqs. (49) and (55) for \(h_{16},h_{26}\) and \(R_{6}\).
Superscripts B, R2M refer to bilateral monopoly and One-retailer–two-manufacturers vertical channel, respectively.
This result is in line with [24].
References
Bass F (1969) A new product growth model for consumer durables. Manag Sci 15(5):215–227
Benchekroun H, Martín-Herrán G, Taboubi S (2009) Could myopic pricing be a strategic choice in marketing channels? A game theoretic analysis. J Econ Dyn Control 33(9):1699–1718
Choi CS (1991) Price competition in a channel structure with a common retailer. Market Sci 10(4):271–296
Choi CS (1996) Price competition in a duopoly common retailer channel. J Retail 72(2):117–134
Coughlan A (1987) Distribution channel choice in a market with complementary goods. Int J Res Market 4:85–97
Dean J (1950) Pricing policies for new products. Harv Bus Rev 18:45–56
Dockner EJ (1985) Optimal pricing in a dynamic duopoly game model. Z für Op Res 29:1–6
Dockner EJ, Gaunersdofer A (1996) Strategic new product pricing when demand obeys saturation effects. Eur J Op Res 90:589–598
Dockner EJ, Jørgensen S (1988) Optimal pricing strategies for new products in dynamic oligopolies. Market Sci 7:315–334
Eliashberg J, Jeuland AP (1986) The impact of competitive entry in a developing market upon dynamic pricing strategies. Market Sci 5:20–36
Fibich G, Gavious A, Lowengart O (2003) Explicit solutions of optimization models and differential games with nonsmooth (asymmetric) reference-price effects. Op Res 51:721–734
Fibich G, Gavious A, Lowengart O (2007) Optimal price promotion in the presence of asymmetric reference-price effects. Manage Decis Econ 28:569–577
Ingene CA, Taboubi S, Zaccour G (2012) Game-theoretic coordination mechanisms in distribution channels: integration and extensions for models without competition. J Retail 88:476–496
Jørgensen S, Zaccour G (2004) Differential games in marketing. International series in quantitative marketing. Kluwer Academic Publishers, Massachusetts
Kalish S (1983) Monopolist pricing with dynamic demand and production costs. Market Sci 2:135–160
Mahajan V, Muller E (1991) Pricing and diffusion of primary and contingent products. Technol Forecast Soc Change 39:291–307
Minowa Y, Choi SC (1995) Optimal pricing strategies for primary and contingent products under duopoly environment. In: Jorgensen S, Zaccour G (eds) Proceedings of the international workshop on dynamic competitive analysis in marketing, pp 235-240
McGuire T, Staelin R (1983) An industry equilibrium analysis of downstream vertical integration. Market Sci 2(2):161–192
Martín-Herrán G, Taboubi S (2015) Price coordination in distribution channels: a dynamic perspective. Eur J Op Res 240:401–414
Martín-Herrán G, Taboubi S, Zaccour G (2012) Dual role of price and myopia in a marketing channel. Eur J Op Res 219(2):284–295
Nerlove M, Arrow KJ (1962) Optimal advertising policy under dynamic conditions. Economica 29:129–142
Popescu I, Wu Y (2007) Dynamic pricing strategies with reference effects. Op Res 55(3):413–429
Robinson B, Lakhani C (1975) Dynamic price models for new-product planning. Manage Sci 21:1113–1122
Simon H, Jacquet F, Brault F (2005) La Stratégie Prix, Dunod (2ième Édition), Paris
Trivedi M (1998) Marketing channels: an extension of exclusive retailership. Manage Sci 44(7):896–909
Author information
Authors and Affiliations
Corresponding author
Additional information
F. Ngendakuriyo: The project was initiated during the post-doctorate at GERAD.
Research supported by NSERC, Canada.
The authors wish to thank the two anonymous Reviewers for their constructive comments.
Appendix
Appendix
1.1 Appendix A
The sufficient condition for a stationary feedback Stackelberg equilibrium requires us to find bounded and continuously differentiable functions, \(V_{R}(x)\) and \(V_{M}(x)\) for the retailer and the manufacturer, respectively, which satisfy for all \(x(t)\geqslant 0\), the HJB equations obtained after the substitution of (10) and (8) into Eqs (7) and (9).
Guided by the model’s linear-quadratic structure, we conjecture that the functions \(V_{R}(x)\) and \(V_{M}(x)\) are quadratic and given by the expressions (13) and (14) in the proposition. The coefficients \(\beta _{1},\beta _{2},\beta _{0},\alpha _{1},\alpha _{2}\) and \(\alpha _{0}\) are obtained by identification after replacing \(V_{R}(x)\) and \(V_{M}(x)\) as well as their first derivatives into the HJB equations.
Finally, plugging the derivatives of these values functions into the expressions (10) and (8) provides the channel members’ pricing strategies at the equilibrium displayed in the proposition.
The terminal conditions
are sufficient conditions guaranteeing that the expressions (13) and (14) are the retailer’s and manufacturer’s value functions and that (11)–(12) are the pricing strategies.
1.2 Appendix B
As in the previous scenario, after computing the retailer’s reaction functions, we move to the manufacturer’s problems. We consider that both manufacturers play à la Nash. In other words, they solve their optimization problems simultaneously. The manufacturer i’s HJB equations are:
Substituting (24) and (25) into (41), the HJB equations of the leaders, and performing the maximization of the right-hand side provide the strategies:
where \(\lambda _{1}=a_{2}\gamma +2\kappa (a_{1}+c\kappa )\) and \(\lambda _{2}=a_{1}\gamma +2\kappa (a_{2}+c\kappa ).\)
Substituting \(p_{Ri}\) and \(p_{Mi}\), namely (24), (25), (42), 43), into the HJB Eqs. (23) and (41) leads to conjecture the quadratic value functions in Eqs. (30) and (31).
We replace \(V_{Mi}(x_{1},x_{2})\) as well as their first derivatives in the HJB equations. To identify the value function coefficients \(h_{ij}\) for \(i=1,2\) and \(j=1,2,...,6\) for manufacturers, we need to solve the twelve Ricatti equations (not printed here). Their canonical forms are the following, for \(i=1,2\); \(\forall i\ne j\):
The value function coefficients for the retailer, \(R_{i}\) for \(i=1,2,....,6\), are identified through the six Ricatti equations below.
We compute the pricing strategies of all channel members by substituting the derivatives of the value functions into expressions (42), (43), (24) and (25). where
The transversality condition
guarantees that the expressions (30), (31); and (26), (27), (28) and (29) are the manufacturer i’s and retailer’s value functions, and the pricing strategies. Notice that \((x_{1}(t),x_{2}(t)) \) is the solution of the closed-loop dynamics resulting in substitution of (26), (27), (28) and (29) into the dynamic demand (4). We have to solve the following dynamical system:
where
The solution gives the expressions for both products’ cumulative sales rate trajectories \(x_{1}(t)\) and \(x_{2}(t)\) given in the proposition. The paths for the pricing strategies are obtained after replacing \(x_{1}(t)\) and \(x_{2}(t)\) by their expressions (32) and (33) in (26), (27), (28) and (29).
Rights and permissions
About this article
Cite this article
Ngendakuriyo, F., Taboubi, S. Pricing Strategies of Complementary Products in Distribution Channels: A Dynamic Approach. Dyn Games Appl 7, 48–66 (2017). https://doi.org/10.1007/s13235-016-0181-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13235-016-0181-7