Matching, Imitation, and Coordination in Networks

Abstract

This paper develops a coevolutionary model of social coordination and matching in which agents are embedded in an arbitrary fixed network and are matched in pairs to play a coordination game. In each period, based on payoff comparison with their neighbors, agents decide whether to imitate their neighbors’ actions and whether to end their present partnerships. Inertia exists in action revision and partnership updating. Each agent can exit a partnership unilaterally. All separated agents are randomly matched in pairs at the beginning of the next period. Occasionally, agents make mistakes in action revision and partnership updating. When the size of the society is large, in the long run, all agents will play the Pareto-efficient action for a particular subset of networks.

Appendix

1.1 Radius–Coradius Theorem

Here, we present the modified radius-coradius theorem of Ellison [12]. Some preliminary definitions are necessary. Consider the perturbed dynamics $(\{X^{\epsilon }(t)\}_{t\in {\mathbb {N}}},S)$, $\epsilon \in (0,1)$. For any $\epsilon$, $\epsilon \in (0,1)$, $\{X^{\epsilon }(t)\}_{t\in {\mathbb {N}}}$ is an irreducible Markov chain. For any two states s and $s^{'}$, the resistance is defined as

$$\begin{aligned} r(s,s^{'})=\lim _{\epsilon \rightarrow 0}\frac{\log \text {Prob}\{X^{\epsilon }(t+1)=s^{'}|X^{\epsilon }(t)=s\}}{\log \epsilon }. \end{aligned}$$

For any two subset ${\bar{\varOmega }}$ and ${\bar{\varOmega }}^{'}$ of $\varOmega$, ${\bar{\varOmega }}\cap {\bar{\varOmega }}^{'}=\emptyset$, a path from ${\bar{\varOmega }}$ to ${\bar{\varOmega }}^{'}$ is a sequence of distinct states $(s^{1}, \ldots ,s^{m})$ with $s^{1}\in {\bar{\varOmega }}$, $s^{l}\notin {\bar{\varOmega }}^{'}$ for $2\le l\le m-1$ and $s^{m}\in {\bar{\varOmega }}^{'}$. Define the resistance of the path $(s^{1}, \ldots ,s^{m})$ as

$$\begin{aligned} r(s^{1}, \ldots ,s^{m})=\sum _{1\le l\le (m-1)} r(s^{l},s^{l+1}). \end{aligned}$$

Let $\mathbf {\text {P}}({\bar{\varOmega }},{\bar{\varOmega }}^{'})$ be the set of all paths from ${\bar{\varOmega }}$ to ${\bar{\varOmega }}^{'}$.

For any absorbing set ${\bar{\varOmega }}$, the radius$R({\bar{\varOmega }})$ is

$$\begin{aligned} R({\bar{\varOmega }})=\min _{(s^{1}, \ldots ,s^{m})\in \mathbf {\text {P}}({\bar{\varOmega }}, \varOmega {\setminus } D({\bar{\varOmega }}))} r(s^{1}, \ldots ,s^{m}). \end{aligned}$$

If a path $(s^{1}, \ldots ,s^{m})$ passes through absorbing sets ${\bar{\varOmega }}^{1}, \ldots ,{\bar{\varOmega }}^{k}$, the modified-resistance is

$$\begin{aligned} r^{*}(s^{1}, \ldots ,s^{m})= r(s^{1}, \ldots ,s^{m})-\sum _{2\le l\le (k-1)}R(\{{\bar{\varOmega }}^{l}\}). \end{aligned}$$

The notation of modified-resistance can be extended to a point-set concept by setting

$$\begin{aligned} r^{*}(s, {\bar{\varOmega }})=\min _{(s^{1}, \ldots ,s^{m})\in \mathbf {\text {P}}(\{s\},{\bar{\varOmega }})} r^{*}(s^{1}, \ldots ,s^{m}). \end{aligned}$$

For any absorbing set ${\bar{\varOmega }}$, the modified-coradius$CR^{*}({\bar{\varOmega }})$ is defined by

$$\begin{aligned} CR^{*}({\bar{\varOmega }})=\max _{s\notin D({\bar{\varOmega }})} r^{*}(s,{\bar{\varOmega }}). \end{aligned}$$

Theorem 2 in Ellison [12], p.24) shows that for any union of absorbing sets ${\bar{\varOmega }}$, when $R({\bar{\varOmega }})>CR^{*}({\bar{\varOmega }})$, ${\bar{\varOmega }}$ contains all stochastically stable equilibria. Intuitively, if there is less resistance to enter the basin of attraction $D({\bar{\varOmega }})$ than to leave it, ${\bar{\varOmega }}$ is relatively stable against the perturbation of random noises and will be observed most of the time when random noises vanish.

1.2 Proofs

Proof of Theorem 1

The proof consists of two parts. The first part shows that a state is a limit state if and only if the conditions in Theorem 1 are satisfied. The proof of sufficiency is trivial. For the sake of space, we only prove the necessity. The second part proves the convergence of the unperturbed dynamics $\{S(t)\}_{t\in {\mathbb {N}}}$.

$\mathbf {Part}$${\mathbf {I}}$: Characterization of limit states

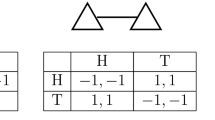
The state $s=((a_{1}, \ldots ,a_{n}),m)$ is an absorbing state if and only if (1) no one is motivated to alter her action and (2) the number of agents who are motivated to end the present partnerships is no more than two. If the number is two, then these two agents are in a partnership. Formally, for any agent $i\in {\mathbf {N}}$, either (i) $u(a_{i},a_{m_{i}})\ge \max _{j\in N(i)}u(a_{j},a_{m_{j}})$ or (ii) $u(a_{i},a_{m_{i}})<\max _{k\in N(i)}u(a_{k},a_{m_{k}})=u(a_{j_{0}},a_{m_{j_{0}}})$ for some neighbor $j_{0}$ with $a_{i}=a_{j_{0}}$. There exists no agent, only one agent $i_{0}$ or two agents $i_{0}$ and $m_{i_{0}}$ satisfying condition (ii). Note that agents play a $2\times 2$ coordination game G with partners. When there are three or more agents satisfying condition (ii), two of them choose the same action, and in the next period, with positive probability, they will be matched to each other and will have no incentive to end the present partnership between them. This behavior implies that the number of agents satisfying condition (ii) can be reduced strictly. Accordingly, the proof of Part ${\mathbf {I}}$ is divided into three cases: no agent, only one agent and two agents satisfying condition (ii). We only focus on the first two cases. The last case can be analyzed similarly.

$\mathbf {Case}$$\mathbf {1}$: $\not \exists i_{0}$ satisfying condition (ii).

This nonexistence means that for any $i\in {\mathbf {N}}$, $u(a_{i},a_{m_{i}})\ge \max _{j\in N(i)}u(a_{j},a_{m_{j}})$. As a result, for any $i,j\in {\mathbf {N}}$, if $g_{ij}=1$, $a_{i}=a_{j}$, and $a_{m_{i}}=a_{m_{j}}$. This result implies that for each component, all members choose the same action, and their partners also choose the same action. Therefore, there is no polymorphic-action component. It is straightforward to conclude that for any component ${\mathbf {c}}$, ${\mathbf {I}}_{A}(s,{\mathbf {c}})={\mathbf {I}}_{B}(s,{\mathbf {c}})=\emptyset$ and ${\mathbf {P}}_{A}(s,{\mathbf {c}})={\mathbf {P}}_{B}(s,{\mathbf {c}})=\emptyset$.

$\mathbf {Case}$$\mathbf {2}$: $\exists$ only one agent $i_{0}$ satisfying condition (ii).

Assume that $i_{0}$ is from the component ${\mathbf {c}}^{'}$. Note that for any $a,a^{'}\in \{A,B\}$, when $a\ne a^{'}$, $u(a,a^{'})<u(a,a)$ holds. It implies that $a_{i_{0}}\ne a_{m_{i_{0}}}$. The uniqueness of $i_{0}$ implies that there exists at most one component ${\mathbf {c}}_{AB}$ such that both actions are played by its members.

The component ${\mathbf {c}}^{'}$ is ${\mathbf {c}}_{AB}$ when ${\mathbf {c}}_{AB}$ exists. Note that in any other component, all members play the same action, and their partners also play the same action. Otherwise, there is at least one more agent satisfying condition (ii). As a result, it must be true that ${\mathbf {c}}_{AB}$ coincides with ${\mathbf {c}}^{'}$. Furthermore, for ${\mathbf {c}}^{'}$, ${\mathbf {I}}_{A}(s,{\mathbf {c}}^{'})={\mathbf {I}}_{B}(s,{\mathbf {c}}^{'})=\emptyset$, ${\mathbf {P}}_{a_{i_{0}}}(s, {\mathbf {c}}^{'})=\{i_{0}\}$ and ${\mathbf {P}}_{a_{m_{i_{0}}}}(s, {\mathbf {c}}^{'})=\emptyset$.

Similarly, when ${\mathbf {c}}_{AB}$ does not exist, then for each component, all members choose the same action. Furthermore,

$$\begin{aligned} \sum _{{\mathbf {c}}\in {\mathbf {C}}} |{\mathbf {P}}_{a_{i_{0}}}(s, {\mathbf {c}})|= |{\mathbf {P}}_{a_{i_{0}}}(s, {\mathbf {c}}^{'})|=1\text { and } \sum _{{\mathbf {c}}\in {\mathbf {C}}} |{\mathbf {P}}_{a_{m_{i_{0}}}}(s, {\mathbf {c}})|=0. \end{aligned}$$

$\mathbf {Part}$$\mathbf {II}$: Convergence of the unperturbed dynamics.

Let $s(t)=\big ({\mathbf {a}}(t),m(t)\big )$ be the state in period t. For any $s\in \varOmega$, let ${\mathbf {N}}_{AA}(s)$ be the set of A-players who are matched to A-players. Note that if $i\in {\mathbf {N}}_{AA}(s)$, then $m(i)\in {\mathbf {N}}_{AA}(s)$. According to whether ${\mathbf {N}}_{AA}(s(0))$ is empty or not, the proof is divided into two cases.

$\mathbf {Case}$$\mathbf {1}$: ${\mathbf {N}}_{AA}(s(0))\ne \emptyset$.

Note that A is the Pareto-efficient action. In period 0, any agent $i\in N({\mathbf {N}}_{AA}(s(0)))$ performs strictly worse than some neighbor in ${\mathbf {N}}_{AA}(s(0))$. In period 1, with strictly positive probability, all agents in $N({\mathbf {N}}_{AA}(s(0)))$ play A, and they are matched into $\lfloor \frac{|N({\mathbf {N}}_{AA}(s(0)))|}{2}\rfloor$ pairs. The remaining agent is matched to a B-player when $|N({\mathbf {N}}_{AA}(s(0)))|$ is odd. Furthermore, all agents in ${\mathbf {I}}_{A}(s(0),{\mathbf {c}}){\setminus } N({\mathbf {N}}_{AA}(s(0)))$ switch from A to B for any ${\mathbf {c}}\in {\mathbf {C}}$. It is straightforward to see that ${\mathbf {N}}_{AA}(s(0))\subseteq {\mathbf {N}}_{AA}(s(1))$ and when $t\ge 1$, ${\mathbf {I}}_{A}(s(t),{\mathbf {c}})=\emptyset$ for any ${\mathbf {c}}\in {\mathbf {C}}$.

Following the same logic, in some period $t_{1}\ge 1$, $\{S(t)\}_{t\in {\mathbb {N}}}$ arrives at a state $s(t_{1})$ where ${\mathbf {N}}_{AA}(s(t_{1}))={\mathbf {N}}_{AA}(s(t_{1}-1))$. The state $s(t_{1})$ is a limit state. When the number of A-players in $s(t_{1})$ is even, all A-players constitute ${\mathbf {N}}_{AA}(s(t_{1}))$; otherwise, at least one A-player is motivated to switch to B, which yields a contradiction. The coincidence of ${\mathbf {N}}_{AA}(s(t_{1}))$ and the set of A-players and the equation ${\mathbf {N}}_{AA}(s(t_{1}))={\mathbf {N}}_{AA}(s(t_{1}-1))$ together imply that each agent plays the same action as her partner; for each B-player, all neighbors play action B. That is, in each component, all members play the same action, and for any $i,j\in {\mathbf {N}}$, if $g_{ij}=1$, $u(a_{i}(t_{1}),a_{m_{i}(t_{1})}(t_{1}))= u(a_{j}(t_{1}),a_{m_{j}(t_{1})}(t_{1}))$. Thus, $s(t_{1})$ is a limit state. When the number of A-players in $s(t_{1})$ is odd, all A-players except one, denoted by $i_{0}$, constitute ${\mathbf {N}}_{AA}(s(t_{1}))$, and $i_{0}\in N({\mathbf {N}}_{AA}(s(t_{1})))$. The equation ${\mathbf {N}}_{AA}(s(t_{1}))={\mathbf {N}}_{AA}(s(t_{1}-1))$ implies that except $i_{0}$ and her partner, each agent is matched to an agent playing the same action, and for each B-player, all neighbors except $i_{0}$ play action B. Therefore, $u(a_{i}(t_{1}),a_{m_{i}(t_{1})}(t_{1}))\ge \max _{j\in N(i)}u(a_{j}(t_{1}),a_{m_{j}(t_{1})}(t_{1}))$ for any $i\in {\mathbf {N}}{\setminus }\{i_{0},m_{i_{0}}(t_{1})\}$, while neither $i_{0}$ nor her partner is motivated to alter action. Therefore, $s(t_{1})$ is also a limit state.

$\mathbf {Case}$$\mathbf {2}$: ${\mathbf {N}}_{AA}(s(0))=\emptyset$.

In this case, in the initial state, all A-players are matched to B-players and receive a common payoff of zero.

Assume that in the initial state, for each A-player, all neighbors play action A. In any component, all members play the same action, and all A-players are matched to B-players. If there are two or more B-players such that the partner of each is an A-player and one neighbor is matched to a B-player, each of these B-players is motivated to exit from the present partnership. In the initial period, with strictly positive probability, two of these B-players, denoted by $i_{0}$ and $j_{0}$, have the opportunity to update their partnerships. In the next period, with strictly positive probability, only two A-players $m_{i_{0}}(0)$ and $m_{j_{0}}(0)$ are matched to each other. Then, we return to Case 1. If there is a unique B-player satisfying that the partner is an A-player and one neighbor is matched to a B-player, then among all agents, only this B-player wants to exit from the partnership, while nobody is motivated to alter action. The initial state therefore is a limit state.

Assume that there exist two or more A-players such that for each of them, one neighbor plays action B. Each of these A-players receives a strictly lower payoff than some neighbor. This lower payoff implies that she is motivated to exit from the present partnership. In the initial period, with strictly positive probability, two of these A-players only have the opportunity to update their partnerships. In the next period, with strictly positive probability, the two A-players are matched to each other. Thus, we return to Case 1.

Assume that in the initial state, there is a unique A-player, denoted by $i_{1}$, satisfying that one neighbor plays action B. Agent $i_{1}$ receives a strictly lower payoff than some neighbor. In the next period, with strictly positive probability, $i_{1}$ switches to action B. For the state s(1), either the condition in one of the above two paragraph holds, or the condition in this paragraph holds. Following the same logic, after a finite number of periods, only the condition in one of the above two paragraph holds. $\square$

Proof of Theorem 2

Assume that there is a limit state $s=((a_{1}, \ldots ,a_{n}),m)$ such that both actions coexist in a widely connected component ${\mathbf {c}}=\big ({\mathbf {N}}^{'},(g_{ij}) _{i,j\in {\mathbf {N}}^{'}}\big )$. Let ${\mathbf {N}}_{a}(s)$ denote the set of all a-players for any $a\in \{A,B\}$. Theorem 1 shows that ${\mathbf {P}}_{A}(s,{\mathbf {c}})$ is nonempty. Furthermore, the discussion Theorem 1 implies that there exist at least two A-players in ${\mathbf {c}}$; that is, $|{\mathbf {N}}^{'}\cap {\mathbf {N}}_{A}(s)|\ge 2$.

Let $\mathbf {B}(s,{\mathbf {c}})$ denote the set of A-players in ${\mathbf {c}}$ who have neighbors playing B. Formally,

$$\begin{aligned} \mathbf {B}(s,{\mathbf {c}})= \{i\in {\mathbf {c}}: a_{i}=A \text { and }\exists j\in N(i)\ a_{j}=B\}. \end{aligned}$$

It is straightforward to see that

$$\begin{aligned} \mathbf {B}(s,{\mathbf {c}})=N({\mathbf {N}}^{'}\cap {\mathbf {N}}_{B}(s))=N({\mathbf {N}}^{'}{\setminus }({\mathbf {N}}^{'}\cap {\mathbf {N}}_{A}(s))). \end{aligned}$$

Note that $|{\mathbf {N}}^{'}\cap {\mathbf {N}}_{A}(s)|\ge 2$. The wide connectedness of ${\mathbf {c}}$ shows that $|\mathbf {B}(s,{\mathbf {c}})|=|N({\mathbf {N}}^{'}{\setminus }({\mathbf {N}}^{'}\cap {\mathbf {N}}_{A}(s)))|\ge 2$. In addition, following from the fact that s is a limit state, ${\mathbf {P}}_{A}(s,{\mathbf {c}})=\mathbf {B}(s,{\mathbf {c}}_{AB})$ holds. Theorem 1 shows that ${\mathbf {P}}_{A}(s,{\mathbf {c}})$ is a singleton, which yields a contradiction. $\square$

Proof of Lemma 1

Assume that the initial state is $\displaystyle \big ((B,B, \ldots ,B),m\big )\in \varOmega _{B}$. In the initial period, only agents $i_{0}$ and $m_{i_{0}}$ receive the opportunity of action revision and switch from B to A by mistake. No one is provided with the opportunity to update her partnership.

In the next period, both agents $i_{0}$ and $m_{i_{0}}$ obtain the highest possible payoff of 1 from the interaction. In the following periods, each of these two agents has no incentive to either switch to B or end the partnership between them.

Following the same logic as in the Proof of Theorem 1, after a finite number of periods, with probability one, $\{S^{\epsilon }(t)\}_{t\in {\mathbb {N}}}$ will arrive at a limit state in $\varOmega _{A}$. $\square$

To facilitate the Proof of Lemma 2, we introduce the following notation. The distance between any two matchings m and $m^{'}$ is defined as the number of partnerships between different pairs of agents. Formally,

$$\begin{aligned} d(m,m^{'})\doteq \frac{|\{i\in {\mathbf {N}}:m_{i}\ne m^{'}_{i}\}|}{2}. \end{aligned}$$

It is straightforward to see that two matchings m and $m^{'}$ are identical if and only if $d(m,m^{'})=0$, and for any two distinct matchings m and $m^{'}$, $d(m,m^{'})\ge 2$.

Proof of Lemma 2

We only focus on the case that $\lambda \le 1$. The case that $\lambda >1$ can be analyzed in a similar manner. Let s denote $((a,a, \ldots ,a),m)$, and let $s^{'}$ denote $((a,a, \ldots ,a),m^{'})$. Assume that the initial state is s.

Let ${\mathbf {N}}_{p}(m,m^{'})$ be the set of agents whose partners are different in m and $m^{'}$. Formally, ${\mathbf {N}}_{p}(m,m^{'})\doteq \{i\in {\mathbf {N}}:m_{i}\ne m^{'}_{i}\}$. It is straightforward to see that $|{\mathbf {N}}_{p}(m,m^{'})|=2\times d(m,m^{'})$.

In the initial period, no one receives the opportunity of action revision, and only $i_{0}$ and $m^{'}_{i_{0}}$, $i_{0}\in {\mathbf {N}}_{p}(m,m^{'})$, receive the opportunity of partnership updating. By two partnership mutations, $i_{0}$ and $m^{'}_{i_{0}}$ end their partnerships in m.

Following the unperturbed behavior rule, in the next period, with strictly positive probability, $i_{0}$ and $m^{'}_{i_{0}}$ form a partnership, and $m_{i_{0}}$ and $m_{m^{'}_{i_{0}}}$ form a partnership. Therefore, another limit state $((a,a, \ldots ,a),\tilde{m})\in \varOmega ^{a}$ is arrived at where (1) $\tilde{m}_{i}=m_{i}$ for any $i\in {\mathbf {N}}{\setminus } \{i_{0},m_{i_{0}},m^{'}_{i_{0}},m_{m^{'}_{i_{0}}}\}$ and (2) $\tilde{m}_{i_{0}}=m^{'}_{i_{0}}$ and $\tilde{m}_{m_{i_{0}}}=m_{m^{'}_{i_{0}}}$. Furthermore, for the matching $\tilde{m}$,

$$\begin{aligned} d(\tilde{m}, m^{'})=\left\{ \begin{array}{l@{\quad }l} d(m, m^{'})-2 &{} \text {if } m^{'}_{m_{i_{0}}}=m_{m^{'}_{i_{0}}};\\ d(m, m^{'})-1 &{} \text {otherwise}.\\ \end{array} \right. \end{aligned}$$

Following the same logic, the sequence $(s_{0}, \ldots ,s_{\ell })$ can be obtained. $\square$