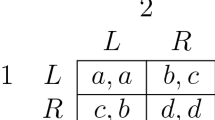Skip to main content

Advertisement

Springer Nature Link
Log in

Heterogeneous Society in Binary Choices with Externalities

  • Published:
Dynamic Games and Applications Aims and scope Submit manuscript

Abstract

We study a two-strategy model with negative externalities proposed by Schelling, in a dynamical setting where a society consists of two interacting populations with different behaviors derived from experiments with human participants. The resulting dynamics is a three-dimensional piecewise smooth map with one discontinuity, which inherits some of the characteristics of each homogeneous population dynamics, while others are lost and new ones emerge. We propose a technique to represent the dynamics on a bidimensional space and prove that the heterogeneous society dynamics can be obtained as a linear combination of the dynamics of the two homogeneous populations. As expected, complexity arises with respect to some aspects. Firstly, the number of equilibria expands to infinity and we were able to determine possible focal equilibria in the sense of Schelling. Secondly, when heterogeneity is introduced, the period adding structure of cycles is replaced by a period incrementing structure. Thirdly, the phenomenon of overreaction and cyclic oscillations can be mitigated even if it never completely disappears. We also derive the orbits of cycles of period two and provide numerical evidences of coexistence of cycles with different periods. It is worth noticing that with the heterogeneous society, the dynamics does not depend on the society aggregate choices only, rather on each population choice; neglecting it will make impossible to determine the future evolution of the system. The implications are important as heterogeneity makes the system path-dependent and a policy maker, considering aggregate society choice only, would be unable to make the proper decisions, unless further information is considered.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

Notes

  1. Thomas C. Schelling–Facts”. Nobelprize.org. Nobel Media AB 2014. Web. 10 Nov 2016. http://www.nobelprize.org/nobel_prizes/economic-sciences/laureates/2005/schelling-facts.html.

  2. In this paper we use the same terminology as in the Population Games literature, see [37, p. 3].

  3. The careful reader will notice that in [8] the choices are labeled A and B, respectively, and that regions are determined by the payoff intersection point d which coincides with \(z^{*}\) as defined in (3).

  4. For the sake of brevity in the following proposition we omit subscript t.

  5. The small difference in terms of notation has to be attributed to the fact that in [8] the dynamics is studied by considering agents choosing L instead of R.

  6. Both these diagrams and Fig. 7 diagrams are in the parameters space \(\left( \delta _L,\delta _R\right) \). However, in Fig. 7 colors represent the period k of cycles, while in Fig. 12 they represent the number of coexistent cycles.

References

  1. Agiza H, Elsadan A (2003) Nonlinear dynamics in the Cournot duopoly game with heterogeneous players. Phys A 320:512–524

    Article  MathSciNet  MATH  Google Scholar 

  2. Alós-Ferrer C (1999) Dynamical systems with a continuum of randomly matched agents. J Econ Theory 86(2):245–267. https://doi.org/10.1006/jeth.1999.2522

    Article  MathSciNet  MATH  Google Scholar 

  3. Arthur WB (2013) Complexity economics: A different framework for economic thought

  4. Avrutin V, Granados A, Schanz M (2011) Sufficient conditions for a period incrementing big bang bifurcation in one-dimensional maps. Nonlinearity 24(9):2575. http://stacks.iop.org/0951-7715/24/i=9/a=012. Accessed 25 June 2018

  5. Avrutin V, Dibak C, Dal Forno A, Merlone U (2015) Dynamics of a \(2\)d piecewise linear Braess paradox model: effect of the third partition. Int J Bifurc Chaos 25(11):1530031

    Article  MathSciNet  MATH  Google Scholar 

  6. Bischi GI, Merlone U (2009) Global dynamics in binary choice models with social influence. J Math Sociol 33(4):277–302

    Article  MATH  Google Scholar 

  7. Bischi GI, Merlone U (2017) Evolutionary minority games with memory. J Evolut Econ 27(5):859–875

    Article  Google Scholar 

  8. Bischi GI, Gardini L, Merlone U (2009) Impulsivity in binary choices and the emergence of periodicity. Discrete Dyn Nat Soc 2009: Article ID 407,913, 22 pages. https://doi.org/10.1155/2009/407913

  9. Bischi GI, Gardini L, Merlone U (2009b) Periodic cycles and bifurcation curves for one-dimensional maps with two discontinuities. J Dyn Syst Geom Theor 7(2):101–123

    MathSciNet  MATH  Google Scholar 

  10. Carting AH (1987) The Schelling diagram: on binary choice with externalities. Behav Sci 32(1):4–18

    Article  Google Scholar 

  11. Caulkins JP, Feichtinger G, Grass D, Hartl RF, Kort PM, Novak AJ, Seidl A, Wirl F (2014) A dynamic analysis of Schelling’s binary corruption model: a competitive equilibrium approach. J Optim Theory Appl 161(2):608–625

    Article  MathSciNet  MATH  Google Scholar 

  12. Cavalli F, Naimzada A, Pireddu M (2016) A family of models for Schelling binary choices. Physica A 444:276–296

    Article  MathSciNet  MATH  Google Scholar 

  13. Ciccone A, Costain J (2004) On payoff heterogeneity in games with strategic complementarities. Oxford Econ Pap 56(4):701–713

    Article  Google Scholar 

  14. Colman AM, Thomas C (2006) Schelling’s psychological decision theory: introduction to a special issue. J Econ Psychol 27:603–608

    Article  Google Scholar 

  15. Costa VD, Tran VL, Turchi J, Averbeck BB (2014) Equity theory and time: a reformulation. Behav Neurosci 128(5):556–566

    Article  Google Scholar 

  16. Dal Forno A, Merlone U (2013) Border-collision bifurcations in a model of Braess paradox. Math Comput Simul 87:1–18

    Article  MathSciNet  Google Scholar 

  17. Dal Forno A, Merlone U (2013b) Replicating human interaction in Braess paradox. In: Pasupathy R, Kim SH, A Tolk RH, Kuhl ME (eds) Proceedings of the 2013 Winter Simulation Conference, Institute of Electrical and Electronics Engineers, Inc., Piscataway, New Jersey

  18. Dal Forno A, Gardini L, Merlone U (2012) Ternary choices in repeated games and border collision bifurcations. Chaos, Solitons Fractals 45(3):294–305. https://doi.org/10.1016/j.chaos.2011.12.003

    Article  MathSciNet  MATH  Google Scholar 

  19. Dal Forno A, Merlone U, Avrutin V (2014) Dynamics in Braess paradox with non-impulsive commuters. Discrete Dyn Nat Soc 2014: Article ID 345, 795

  20. Devaney R (1989) An introduction to Chaotic Dynamical Systems, 2nd edn. Perseus Books, Reading

  21. Feudel U (2008) Complex dynamics in multistable systems. Int J Bifurc Chaos 18(06):1607–1626

    Article  MathSciNet  Google Scholar 

  22. Feudel U, Grebogi C (1997) Multistability and the control of complexity. Chaos: an Interdisciplinary. J Nonlinear Sci 7(4):597–604

    MATH  Google Scholar 

  23. Gigerenzer G (2008) Why heuristics work. Perspect Psychol Sci 3(1):20–29. https://doi.org/10.1111/j.1745-6916.2008.00058.x

    Article  Google Scholar 

  24. Golman R (2011) Why learning doesn’t add up: equilibrium selection with a composition of learning rules. Int J Game Theory 40(4):719–733

    Article  MathSciNet  MATH  Google Scholar 

  25. Grissom RJ, Kim J (2012) Effect sizes for research. Routledge, New York

    Google Scholar 

  26. Harrison JM, Kreps DM (1978) Speculative investor behavior in a stock market with heterogeneous expectations. Q J Econ 92(2):323–336

    Article  MATH  Google Scholar 

  27. Hertwig R, Hoffrage U (1965) Simple heuristics: the foundations of adaptive social behaviour. In: Hertwig R, Hoffrage U, ABC Research Group (eds) Simple heuristics in a social world, Oxford University Press, Oxford, pp 3–36

  28. Hinson JM, Jameson TL, Whitney P (2003) Impulsive decision making and working memory. J Exp Psychol Learn Mem Cogn 29(2):289–306

    Article  Google Scholar 

  29. Hommes C (2006) Heterogeneous agent models in economics and finance. In: Tesfatsion L, Judd KL (eds) Handbook of computational economics, vol 2. Agent-based computational economics. Elsevier Science, Amsterdam, NL, pp 1109–1186

    Google Scholar 

  30. Kirman A (2006) Heterogeneity in economics. J Econ Interac Coord 1(1):89–117

    Article  Google Scholar 

  31. Kline P (2010) Place based policies, heterogeneity, and agglomeration. Am Econ Rev 100(2):383–387

    Article  Google Scholar 

  32. Nerlove M (2014) Individual heterogeneity and state dependence: from George Biddell Airy to James Joseph Heckman. Œconomia 4:281–320

    Google Scholar 

  33. Parchomovsky G, Siegelman P (2012) Cities, property, and positive externalities. William Mary Law Rev 54(1):211–260

    Google Scholar 

  34. Pennings JME, Garcia P (2004) Hedging behavior in small and medium-sized enterprises: the role of unobserved heterogeneity. J Bank Finance 28(5):951–978

    Article  Google Scholar 

  35. Phan D (2007) Heterogeneous agents with local social influence networks: Path dependence and plurality of equilibria in the ace noiseless case. In: Consiglio A (ed) Artificial markets modeling: methods and applications. Springer, Berlin, pp 181–194

    Chapter  Google Scholar 

  36. Platteau JP, Strzalecki T (2004) Collective action, heterogeneous loyalties and path dependence: micro-evidence from senegal. J Afr Econ 13(3):417–445

    Article  Google Scholar 

  37. Sandholm WH (2010) Population games and evolutionary dynamics. The MIT Press, Cambridge

    MATH  Google Scholar 

  38. Santos FC, Pacheco JM, Lenaerts T (2006) Evolutionary dynamics of social dilemmas in structured heterogeneous populations. Proc Natl Acad Sci USA 103:3490–3494

    Article  Google Scholar 

  39. Schelling TC (1960) The strategy of conflict. Harvard University Press, Cambridge

    MATH  Google Scholar 

  40. Schelling TC (1973) Hockey helmets, concealed weapons, and daylight saving. J Conflict Resolut 17:381–428

    Article  Google Scholar 

  41. Schelling TC (1978) Micromotives and macrobehavior. W. W, Norton, New York

    Google Scholar 

  42. Schmid AA (2008) Conflict and cooperation: institutional and behavioral economics. Blackwell Publishing, Oxford

    Google Scholar 

  43. Siegel S, Goldstein DA (1959) Decision making behavior in a two-choice uncertain outcome situation. J Exp Psychol 57:37–42

    Article  Google Scholar 

  44. Weibull J (1997) Evolutionary Game Theory. MIT Press, Cambridge

    MATH  Google Scholar 

Download references

Acknowledgements

The authors are grateful to Gian-Italo Bischi, Laura Gardini, Amnon Rapoport, the participants to the June, 8th, 2011 seminar at Centro de Modelamiento Matemático, Universidad de Chile and the participants to the 46th Annual Meeting of the Society of Mathematical Psychology in Potsdam, for helpful suggestions and constructive discussions. Usual caveats apply. This work has been performed within the activity of the PRIN project “Local interactions and global dynamics in economics and finance: models and tools”, MIUR, Italy, and under the auspices of COST Action IS1104 “The EU in the new complex geography of economic systems: models, tools and policy evaluation”.

Author information

Authors and Affiliations

  1. Department of Economics, University of Molise, Via Francesco De Sanctis, snc, 86100, Campobasso, Italy

    Arianna Dal Forno

  2. Department of Psychology, Center for Logic, Language, and Cognition, University of Torino, Via Verdi 10, 10124, Torino, Italy

    Ugo Merlone

Authors
  1. Arianna Dal Forno
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ugo Merlone
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Ugo Merlone.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dal Forno, A., Merlone, U. Heterogeneous Society in Binary Choices with Externalities. Dyn Games Appl 9, 433–457 (2019). https://doi.org/10.1007/s13235-018-0270-x

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13235-018-0270-x

Keywords