Skip to main content

Advertisement

Springer Nature Link
Log in

Game-Theoretic Frameworks for Epidemic Spreading and Human Decision-Making: A Review

  • Published:
Dynamic Games and Applications Aims and scope Submit manuscript

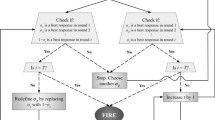
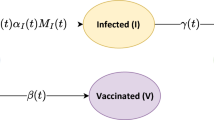
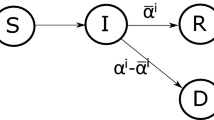
Abstract

This review presents and reviews various solved and open problems in developing, analyzing, and mitigating epidemic spreading processes under human decision-making. We provide a review of a range of epidemic models and explain the pros and cons of different epidemic models. We exhibit the art of coupling between epidemic models and decision models in the existing literature. More specifically, we provide answers to fundamental questions in human decision-making amid epidemics, including what interventions to take to combat the disease, who are decision-makers, and when and how to take interventions, and how to make interventions. Among many decision models, game-theoretic models have become increasingly crucial in modeling human responses or behavior amid epidemics in the last decade. In this review, we motivate the game-theoretic approach to human decision-making amid epidemics. This review provides an overview of the existing literature by developing a multi-dimensional taxonomy, which categorizes existing literature based on multiple dimensions, including (1) types of games, such as differential games, stochastic games, evolutionary games, and static games; (2) types of interventions, such as social distancing, vaccination, quarantine, and taking antidotes; (3) the types of decision-makers, such as individuals, adversaries, and central authorities at different hierarchical levels. A fine-grained dynamic game framework is proposed to capture the essence of game-theoretic decision-making amid epidemics. We showcase three representative frameworks with unique ways of integrating game-theoretic decision-making into the epidemic models from a vast body of literature. Each of the three frameworks has their unique way of modeling and analyzing and develops results from different angles. In the end, we identify several main open problems and research gaps left to be addressed and filled.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Abouelkheir I, El Kihal F, Rachik M, Elmouki I (2019) Optimal impulse vaccination approach for an sir control model with short-term immunity. Mathematics 7(5):420

    Google Scholar 

  2. Adiga A, Venkat S, Vullikanti A (2016) To delay or not: temporal vaccination games on networks. In: IEEE INFOCOM 2016—the 35th annual IEEE international conference on computer communications. IEEE, pp 1–9

  3. Akhil P, Altman E, Sundaresan R, LINCS P (2019) A mean-field approach for controlling singularly perturbed multi-population sis epidemics. arXiv preprint arXiv:1902.05713

  4. Ali A, Altman E, Chahed T, Fiems D, Panda M, Sassatelli L (2012) Estimating file-spread in delay tolerant networks under two-hop routing. In: International conference on research in networking. Springer, pp 277–290

  5. Allen E (2007) Modeling with Itô stochastic differential equations, vol 22. Springer, Berlin

    MATH  Google Scholar 

  6. Allen LJ (2008) An introduction to stochastic epidemic models. In: Brauer F, van den Driessche P, Wu J (eds) Mathematical epidemiology. Springer, Berlin, pp 81–130

    Google Scholar 

  7. Altman E (2012) An epidemic game between contents in a wireless network. In: 2012 international symposium on wireless communication systems (ISWCS). IEEE, pp 1088–1091

  8. Altman E (2013) A stochastic game approach for competition over popularity in social networks. Dyn Games Appl 3(2):313–323

    MathSciNet  MATH  Google Scholar 

  9. Altman E, Başar T, De Pellegrini F (2010) Optimal monotone forwarding policies in delay tolerant mobile ad-hoc networks. Perform Eval 67(4):299–317

    Google Scholar 

  10. Amaral MA, de Oliveira MM, Javarone MA (2021) An epidemiological model with voluntary quarantine strategies governed by evolutionary game dynamics. Chaos Solitons Fractals 143:110616

    MathSciNet  Google Scholar 

  11. Andersson H, Britton T (2012) Stochastic epidemic models and their statistical analysis, vol 151. Springer, Berlin

    MATH  Google Scholar 

  12. Ansumali S, Kaushal S, Kumar A, Prakash MK, Vidyasagar M (2020) Modelling a pandemic with asymptomatic patients, impact of lockdown and herd immunity, with applications to sars-cov-2. Annu Rev Control

  13. Aurell A, Carmona R, Dayanikli G, Lauriere M (2020) Optimal incentives to mitigate epidemics: a Stackelberg mean field game approach. arXiv preprint arXiv:2011.03105

  14. Bagagiolo F, Bauso D (2014) Mean-field games and dynamic demand management in power grids. Dyn Games Appl 4(2):155–176

    MathSciNet  MATH  Google Scholar 

  15. Başar T, Olsder GJ (1998) Dynamic noncooperative game theory. SIAM, Philadelphia

    MATH  Google Scholar 

  16. Bauch CT, Earn DJ (2004) Vaccination and the theory of games. Proc Natl Acad Sci 101(36):13391–13394

    MathSciNet  MATH  Google Scholar 

  17. Bernoulli D (1760) Essai d’une nouvelle analyse de la mortalité causée par la petite vérole, et des avantages de l’inoculation pour la prévenir. Histoire de l’Acad., Roy. Sci.(Paris) avec Mem, pp 1–45

  18. Bhattacharyya S, Bauch C (2010) A game dynamic model for delayer strategies in vaccinating behaviour for pediatric infectious diseases. J Theor Biol 267(3):276–282

    MathSciNet  MATH  Google Scholar 

  19. Bieck C, Marshall A (2020) Redirecting resources to promote post-pandemic growth. Strategy & Leadership

  20. Blume L, Easley D, Kleinberg J, Kleinberg R, Tardos É (2013) Network formation in the presence of contagious risk. ACM Trans Econ Comput 1(2):1–20

    Google Scholar 

  21. Breban R, Vardavas R, Blower S (2007) Mean-field analysis of an inductive reasoning game: application to influenza vaccination. Phys Rev E 76(3):031127

    Google Scholar 

  22. Cator E, Van Mieghem P (2012) Second-order mean-field susceptible-infected-susceptible epidemic threshold. Phys Rev E 85(5):056111

    Google Scholar 

  23. Chang SL, Piraveenan M, Pattison P, Prokopenko M (2020) Game theoretic modelling of infectious disease dynamics and intervention methods: a review. J Biol Dyn 14(1):57–89

    MathSciNet  MATH  Google Scholar 

  24. Chapman GB, Li M, Vietri J, Ibuka Y, Thomas D, Yoon H, Galvani AP (2012) Using game theory to examine incentives in influenza vaccination behavior. Psychol Sci 23(9):1008–1015

    Google Scholar 

  25. Chen J, Huang Y, Zhang R, Zhu Q (2021) Optimal curing strategy for competing epidemics spreading over complex networks. IEEE Trans Signal Inf Process Netw. https://doi.org/10.1109/TSIPN.2021.3075338

    Article  MathSciNet  Google Scholar 

  26. Chimmula VKR, Zhang L (2020) Time series forecasting of Covid-19 transmission in Canada using LSTM networks. Chaos Solitons Fractals 135:109864

    Google Scholar 

  27. Dashtbali M, Malek A, Mirzaie M (2020) Optimal control and differential game solutions for social distancing in response to epidemics of infectious diseases on networks. Optim Control Appl Methods 41(6):2149–2165

    MathSciNet  MATH  Google Scholar 

  28. Di Lauro F, Kiss IZ, Rus D, Della Santina C (2020) Covid-19 and flattening the curve: a feedback control perspective. IEEE Control Syst Lett 5(4):1435–1440

    MathSciNet  Google Scholar 

  29. Draief M, Massoulie L (2009) Epidemics and rumours in complex networks. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  30. Eksin C (2019) Control of stochastic disease network games via influential individuals. In: 2019 IEEE 58th conference on decision and control (CDC). IEEE, pp 6893–6898

  31. Eksin C, Shamma JS, Weitz JS (2017) Disease dynamics in a stochastic network game: a little empathy goes a long way in averting outbreaks. Sci Rep 7(1):1–13

    Google Scholar 

  32. Erdem M, Safan M, Castillo-Chavez C (2017) Mathematical analysis of an SIQR influenza model with imperfect quarantine. Bull Math Biol 79(7):1612–1636

    MathSciNet  MATH  Google Scholar 

  33. Fall A, Iggidr A, Sallet G, Tewa JJ (2007) Epidemiological models and Lyapunov functions. Math Model Nat Phenom 2(1):62–83

    MathSciNet  MATH  Google Scholar 

  34. Farhadi F, Tavafoghi H, Teneketzis D, Golestani SJ (2019) An efficient dynamic allocation mechanism for security in networks of interdependent strategic agents. Dyn Games Appl 9(4):914–941

    MathSciNet  MATH  Google Scholar 

  35. Feng Y, Ding L, Huang YH, Guan ZH (2016) Epidemic spreading on random surfer networks with infected avoidance strategy. Chin Phys B 25(12):128903

    Google Scholar 

  36. Feng Y, Ding L, Huang YH, Zhang L (2016) Epidemic spreading on weighted networks with adaptive topology based on infective information. Physica A 463:493–502

    MathSciNet  MATH  Google Scholar 

  37. Fisher M (2020) Why coronavirus conspiracy theories flourish. And why it matters. https://www.nytimes.com/2020/04/08/world/europe/coronavirus-conspiracy-theories.html?smid=url-share

  38. Fudenberg D, Tirole J (1991) Game theory. MIT Press, Cambridge

    MATH  Google Scholar 

  39. Funk S, Gilad E, Watkins C, Jansen VA (2009) The spread of awareness and its impact on epidemic outbreaks. Proc Natl Acad Sci 106(16):6872–6877

    MATH  Google Scholar 

  40. Ganesh A, Massoulié L, Towsley D (2005) The effect of network topology on the spread of epidemics. In: Proceedings IEEE 24th annual joint conference of the IEEE computer and communications societies, vol 2. IEEE, pp 1455–1466

  41. Gast N, Gaujal B, Le Boudec JY (2012) Mean field for Markov decision processes: from discrete to continuous optimization. IEEE Trans Autom Control 57(9):2266–2280

    MathSciNet  MATH  Google Scholar 

  42. Goeree JK, Holt CA, Palfrey TR (2010) Quantal response equilibria. In: Behavioural and experimental economics. Springer, pp 234–242

  43. Gosak M, Kraemer MU, Nax HH, Perc M, Pradelski BS (2021) Endogenous social distancing and its underappreciated impact on the epidemic curve. Sci Rep 11(1):1–10

    Google Scholar 

  44. Government TO Ontario COVID-19 Rapid Research Fund. https://www.ontario.ca/page/ontario-covid-19-rapid-research-fund

  45. Granell C, Gómez S, Arenas A (2014) Competing spreading processes on multiplex networks: awareness and epidemics. Phys Rev E 90(1):012808

    Google Scholar 

  46. Gray A, Greenhalgh D, Hu L, Mao X, Pan J (2011) A stochastic differential equation sis epidemic model. SIAM J Appl Math 71(3):876–902

    MathSciNet  MATH  Google Scholar 

  47. Gregorian D (2021) Get vaccinated in Ohio and get a shot at \(\$1\) million, gov. mike Dewine announces. NBC News. https://www.nbcnews.com/politics/politics-news/get-vaccinated-ohio-get-shot-1-million-gov-mike-dewine-n1267176

  48. Grottke M, Avritzer A, Menasché DS, de Aguiar LP, Altman E (2016) On the efficiency of sampling and countermeasures to critical-infrastructure-targeted malware campaigns. SIGMETRICS Perform Eval Rev 43(4):33–42. https://doi.org/10.1145/2897356.2897361

    Article  Google Scholar 

  49. Gubar E, Zhitkova EM, Kupchinenko E, Petriakova N (2015) Two modes of vaccination program in controlled sir model. Contrib Game Theory Manag 8:84–98

    MathSciNet  MATH  Google Scholar 

  50. Hayel Y, Zhu Q (2017) Epidemic protection over heterogeneous networks using evolutionary Poisson games. IEEE Trans Inf Forensics Secur 12(8):1786–1800

    Google Scholar 

  51. Herrera JL, Srinivasan R, Brownstein JS, Galvani AP, Meyers LA (2016) Disease surveillance on complex social networks. PLoS Comput Biol 12(7):e1004928

    Google Scholar 

  52. Horák K, Bošanskỳ B (2019) Solving partially observable stochastic games with public observations. In: Proceedings of the AAAI conference on artificial intelligence, vol 33-01, pp 2029–2036

  53. Hossain MS, Muhammad G, Guizani N (2020) Explainable AI and mass surveillance system-based healthcare framework to combat COVID-I9 like pandemics. IEEE Network 34(4):126–132

    Google Scholar 

  54. Hota AR, Godbole J, Bhariya P, Paré PE (2020) A closed-loop framework for inference, prediction and control of sir epidemics on networks. arXiv preprint arXiv:2006.16185

  55. Hota AR, Sneh T, Gupta K (2020) Impacts of game-theoretic activation on epidemic spread over dynamical networks. arXiv preprint arXiv:2011.00445

  56. Hota AR, Sundaram S (2016) Interdependent security games on networks under behavioral probability weighting. IEEE Trans Control Netw Syst 5(1):262–273

    MathSciNet  MATH  Google Scholar 

  57. Hota AR, Sundaram S (2016) Optimal network topologies for mitigating security and epidemic risks. In: 2016 54th annual Allerton conference on communication, control, and computing (Allerton). IEEE, pp 1129–1136

  58. Hota AR, Sundaram S (2018) Game-theoretic choice of curing rates against networked sis epidemics by human decision-makers. arXiv preprint arXiv:1810.01293

  59. Hota AR, Sundaram S (2019) Game-theoretic vaccination against networked sis epidemics and impacts of human decision-making. IEEE Trans Control Netw Syst 6(4):1461–1472

    MathSciNet  MATH  Google Scholar 

  60. Huang CT, Sakib MN, Njilla L, Kamhoua C (2019) A game theoretic approach for making iot device connectivity decisions during malware outbreak. In: 2019 international conference on computing, networking and communications (ICNC). IEEE, pp 457–462

  61. Huang Y, Chen J, Huang L, Zhu Q (2020) Dynamic games for secure and resilient control system design. Natl Sci Rev 7(7):1125–1141

    Google Scholar 

  62. Huang Y, Ding L, Feng Y (2016) A novel epidemic spreading model with decreasing infection rate based on infection times. Physica A 444:1041–1048

    MathSciNet  MATH  Google Scholar 

  63. Huang Y, Ding L, Feng Y, Pan J (2016) Epidemic spreading in random walkers with heterogeneous interaction radius. J Stat Mech: Theory Exp 2016(10):103501

    MathSciNet  MATH  Google Scholar 

  64. Huang Y, Kavitha V, Zhu Q (2019) Continuous-time Markov decision processes with controlled observations. In: 2019 57th annual Allerton conference on communication, control, and computing (Allerton). IEEE, pp 32–39

  65. Huang Y, Zhu Q (2019) Achieving social optimum in dynamic weight adaptation for virus mitigation: a potential differential game approach. IFAC-PapersOnLine 52(20):241–246

    Google Scholar 

  66. Huang Y, Zhu Q (2020) A differential game approach to decentralized virus-resistant weight adaptation policy over complex networks. IEEE Trans Control Netw Syst 7(2):944–955

    MathSciNet  MATH  Google Scholar 

  67. Ibuka Y, Li M, Vietri J, Chapman GB, Galvani AP (2014) Free-riding behavior in vaccination decisions: an experimental study. PLoS ONE 9(1):e87164

    Google Scholar 

  68. Isaacs R (1999) Differential games: a mathematical theory with applications to warfare and pursuit, control and optimization. Courier Corporation

  69. Johnson M. State attorneys general urge FDA to transition to gender neutral screening for blood donations. https://thehill.com/policy/healthcare/494138-state-attorneys-general-urge-fda-to-transition-to-gender-neutral-screening

  70. Kephart JO, White SR (1992) Directed-graph epidemiological models of computer viruses. In: Computation: the micro and the macro view. World Scientific, pp 71–102

  71. Kermack WO, McKendrick AG (1932) Contributions to the mathematical theory of epidemics. II. The problem of endemicity. Proc R Soc Lond Ser A Contain Pap Math Phys Charact 138(834):55–83

    MATH  Google Scholar 

  72. Khanafer A, Başar T, Gharesifard B (2014) Stability properties of infection diffusion dynamics over directed networks. In: 53rd IEEE conference on decision and control. IEEE, pp 6215–6220

  73. Khouzani M, Sarkar S, Altman E (2011) Saddle-point strategies in malware attack. IEEE J Sel Areas Commun 30(1):31–43

    Google Scholar 

  74. Khouzani M, Sarkar S, Altman E (2012) Maximum damage malware attack in mobile wireless networks. IEEE/ACM Trans Netw 20(5):1347–1360

    Google Scholar 

  75. Köhler J, Schwenkel L, Koch A, Berberich J, Pauli P, Allgöwer F (2020) Robust and optimal predictive control of the covid-19 outbreak. Ann Rev Control

  76. Kryscio RJ, Lefévre C (1989) On the extinction of the S-I-S stochastic logistic epidemic. J Appl Probab 26(4):685–694

    MathSciNet  MATH  Google Scholar 

  77. Kim SB, Yoon M, Ku NS, Kim MH, Song JE, Ahn JY, Jeong SJ, Kim C, Kwon H-D, Lee J (2014) Mathematical modeling of HIV prevention measures including pre-exposure prophylaxis on HIV incidence in South Korea. PloS ONE 9(3):e90080

    Google Scholar 

  78. Lagos AR, Kordonis I, Papavassilopoulos G (2020) Games of social distancing during an epidemic: local vs statistical information. arXiv preprint arXiv:2007.05185

  79. Lee W, Liu S, Tembine H, Li W, Osher S (2021) Controlling propagation of epidemics via mean-field control. SIAM J Appl Math 81(1):190–207

    MathSciNet  MATH  Google Scholar 

  80. Legenvre FX, Hayel Y, Altman E (2016) Potential game approach to virus attacks in network with general topology. In: International conference on network games, control, and optimization. Springer, pp 169–176

  81. Li K, Zhang H, Zhu G, Small M, Fu X (2019) Suboptimal control and targeted constant control for semi-random epidemic networks. IEEE Trans Syst Man Cybern Syst

  82. Li XJ, Li C, Li X (2017) Minimizing social cost of vaccinating network sis epidemics. IEEE Trans Netw Sci Eng 5(4):326–335

    Google Scholar 

  83. Liu X, Lin K, Wang L, Zhang H (2020) Stochastic evolutionary game analysis between special committees and CEO: incentive and supervision. Dyn Games Appl 11:1–18

    MathSciNet  MATH  Google Scholar 

  84. Liu XT, Wu ZX, Zhang L (2012) Impact of committed individuals on vaccination behavior. Phys Rev E 86(5):051132

    Google Scholar 

  85. Maggi L, De Pellegrini F, Reiffers A, Herings PJJ, Altman E (2014) Coordination of epidemic control policies: a game theoretic perspective. In: 2014 7th international conference on NETwork games, control and optimization (NetGCoop). IEEE, pp 180–187

  86. Mahrouf M, Lotfi EM, Hattaf K, Yousfi N (2020) Non-pharmaceutical interventions and vaccination controls in a stochastic SIVR epidemic model. Differ Equ Dyn Syst 1–19

  87. Mai VS, Battou A, Mills K (2018) Distributed algorithm for suppressing epidemic spread in networks. IEEE Control Syst Lett 2(3):555–560

    MathSciNet  Google Scholar 

  88. Masson AR, Hayel Y, Altman E (2017) Posting behavior dynamics and active filtering for content diversity in social networks. IEEE Trans Signal Inf Process Netw 3(2):376–387

    MathSciNet  Google Scholar 

  89. McAlpine K. Game theory and the COVID-19 outbreak: Coordinating our interests at individual to national levels. https://ece.engin.umich.edu/stories/game-theory-and-the-covid-19-outbreak-coordinating-our-interests-at-individual-to-national-levels

  90. Mercer TR, Salit M (2021) Testing at scale during the COVID-19 pandemic. Nat Rev Genet 22:1–12

    Google Scholar 

  91. Muggy L (2021) How game theory could solve the COVID vaccine rollout puzzle. https://fortune.com/2021/03/10/covid-vaccine-rollout-public-health-game-theory/

  92. Muggy L, Stamm JLH (2020) Decentralized beneficiary behavior in humanitarian supply chains: models, performance bounds, and coordination mechanisms. Ann Oper Res 284(1):333–365

    MathSciNet  MATH  Google Scholar 

  93. Nagurney A, Dutta P (2019) Supply chain network competition among blood service organizations: a generalized nash equilibrium framework. Ann Oper Res 275(2):551–586

    MathSciNet  MATH  Google Scholar 

  94. Nåsell I (1996) The quasi-stationary distribution of the closed endemic SIS model. Adv Appl Probab 28(3):895–932

    MathSciNet  MATH  Google Scholar 

  95. Netrapalli P, Sanghavi S (2012) Learning the graph of epidemic cascades. ACM SIGMETRICS Perform Eval Rev 40(1):211–222

    Google Scholar 

  96. Newman M (2010) Networks: an introduction. Oxford University Press, Oxford

    MATH  Google Scholar 

  97. Nowzari C, Preciado VM, Pappas GJ (2016) Analysis and control of epidemics: a survey of spreading processes on complex networks. IEEE Control Syst Mag 36(1):26–46

    MathSciNet  MATH  Google Scholar 

  98. Ogura M, Preciado VM (2016) Efficient containment of exact sir Markovian processes on networks. In: 2016 IEEE 55th conference on decision and control (CDC). IEEE, pp 967–972

  99. Omic J, Orda A, Van Mieghem P (2009) Protecting against network infections: a game theoretic perspective. In: IEEE INFOCOM 2009. IEEE, pp 1485–1493

  100. Panda M, Ali A, Chahed T, Altman E (2014) Tracking message spread in mobile delay tolerant networks. IEEE Trans Mob Comput 14(8):1737–1750

    Google Scholar 

  101. Paré PE, Beck CL, Başar, T (2020) Modeling, estimation, and analysis of epidemics over networks: an overview. Annu Rev Control

  102. Paré PE, Beck CL, Nedić A (2017) Epidemic processes over time-varying networks. IEEE Trans Control Netw Syst 5(3):1322–1334

    MathSciNet  MATH  Google Scholar 

  103. Parino F, Zino L, Porfiri M, Alessandro R (2021) Modelling and predicting the effect of social distancing and travel restrictions on covid-19 spreading. J R Soc Interface 18(175):20200875

    Google Scholar 

  104. Pastor-Satorras R, Vespignani A (2001) Epidemic dynamics and endemic states in complex networks. Phys Rev E 63(6):066117

    Google Scholar 

  105. Pastor-Satorras R, Vespignani A (2001) Epidemic spreading in scale-free networks. Phys Rev Lett 86(14):3200

    Google Scholar 

  106. Patro GK, Chakraborty A, Banerjee A, Ganguly N (2020) Towards safety and sustainability: designing local recommendations for post-pandemic world. In: Fourteenth ACM conference on recommender systems, pp 358–367

  107. Pejó B, Biczók G (2020) Corona games: Masks, social distancing and mechanism design. In: Proceedings of the 1st ACM SIGSPATIAL international workshop on modeling and understanding the spread of COVID-19, pp 24–31

  108. Pezzutto M, Rosselló NB, Schenato L, Garone E (2021) Smart testing and selective quarantine for the control of epidemics. Annu Rev Control

  109. Poletti P, Ajelli M, Merler S (2012) Risk perception and effectiveness of uncoordinated behavioral responses in an emerging epidemic. Math Biosci 238(2):80–89

    MathSciNet  MATH  Google Scholar 

  110. Poletti P, Caprile B, Ajelli M, Pugliese A, Merler S (2009) Spontaneous behavioural changes in response to epidemics. J Theor Biol 260(1):31–40

    MathSciNet  MATH  Google Scholar 

  111. Possieri C, Rizzo A (2019) A mathematical framework for modeling propagation of infectious diseases with mobile individuals. In: 2019 IEEE 58th conference on decision and control (CDC). IEEE, pp 3750–3755

  112. Preciado VM, Zargham M, Enyioha C, Jadbabaie A, Pappas G (2013) Optimal vaccine allocation to control epidemic outbreaks in arbitrary networks. In: 52nd IEEE conference on decision and control. IEEE, pp 7486–7491

  113. Pretorius Carel, Stover John, Bollinger Lori, Bacaër Nicolas, Williams Brian (2010) Evaluating the cost-effectiveness of pre-exposure prophylaxis (PrEP) and its impact on HIV-1 transmission in South Africa. PLoS ONE 5(11):e13646

    Google Scholar 

  114. Reluga TC (2010) Game theory of social distancing in response to an epidemic. PLoS Comput Biol 6(5):e1000793

    MathSciNet  Google Scholar 

  115. Reluga TC, Bauch CT, Galvani AP (2006) Evolving public perceptions and stability in vaccine uptake. Math Biosci 204(2):185–198

    MathSciNet  MATH  Google Scholar 

  116. Rhee I, Shin M, Hong S, Lee K, Kim SJ, Chong S (2011) On the levy-walk nature of human mobility. IEEE/ACM Trans Netw 19(3):630–643

    Google Scholar 

  117. Rieger MO, He-Ulbricht Y (2020) German and Chinese dataset on attitudes regarding COVID-19 policies, perception of the crisis, and belief in conspiracy theories. Data Brief 33:106384

    Google Scholar 

  118. Rothe C, Schunk M, Sothmann P, Bretzel G, Froeschl G, Wallrauch C, Zimmer T, Thiel V, Janke C, Guggemos W et al (2020) Transmission of 2019-NCOV infection from an asymptomatic contact in Germany. N Engl J Med 382(10):970–971

    Google Scholar 

  119. Romer D, Jamieson KH (2020) Conspiracy theories as barriers to controlling the spread of COVID-19 in the US. Soc Sci Med 263:113356

    Google Scholar 

  120. Saha S, Adiga A, Vullikanti AKS (2014) Equilibria in epidemic containment games. In: Proceedings of the twenty-eighth AAAI conference on artificial intelligence, pp 777–783

  121. Samorodnitsky D (2021) An anonymous COVID-19 contact tracing app that warns you when your friends are sick. https://massivesci.com/articles/covid-19-contact-tracing-app-novid-po-shen-loh/

  122. Shen S, Li H, Han R, Vasilakos AV, Wang Y, Cao Q (2014) Differential game-based strategies for preventing malware propagation in wireless sensor networks. IEEE Trans Inf Forensics Secur 9(11):1962–1973

    Google Scholar 

  123. Sparks R, Keighley T, Muscatello D (2011) Optimal exponentially weighted moving average (EWMA) plans for detecting seasonal epidemics when faced with non-homogeneous negative binomial counts. J Appl Stat 38(10):2165–2181

    MathSciNet  MATH  Google Scholar 

  124. Stamm JLH, Serban N, Swann J, Wortley P (2017) Quantifying and explaining accessibility with application to the 2009 H1N1 vaccination campaign. Health Care Manag Sci 20(1):76–93

    Google Scholar 

  125. Tembine H (2020) Covid-19: data-driven mean-field-type game perspective. Games 11(4):51

    MathSciNet  MATH  Google Scholar 

  126. Tembine H, Le Boudec JY, El-Azouzi R, Altman E (2009) Mean field asymptotics of Markov decision evolutionary games and teams. In: 2009 international conference on game theory for networks. IEEE, pp 140–150

  127. Theodorakopoulos G, Le Boudec JY, Baras JS (2012) Selfish response to epidemic propagation. IEEE Trans Autom Control 58(2):363–376

    MathSciNet  MATH  Google Scholar 

  128. Toberts S (2020) The pandemic is a Prisoner’s dilemma game. https://www.nytimes.com/2020/12/20/health/virus-vaccine-game-theory.html?smid=url-share

  129. Trajanovski S, Hayel Y, Altman E, Wang H, Van Mieghem P (2015) Decentralized protection strategies against sis epidemics in networks. IEEE Trans Control Netw Syst 2(4):406–419

    MathSciNet  MATH  Google Scholar 

  130. Trajanovski S, Kuipers FA, Hayel Y, Altman E, Van Mieghem P (2017) Designing virus-resistant, high-performance networks: a game-formation approach. IEEE Trans Control Netw Syst 5(4):1682–1692

    MathSciNet  MATH  Google Scholar 

  131. Tsemogne O, Hayel Y, Kamhoua C, Deugoué G (2021) Game theoretic modeling of cyber deception against epidemic botnets in internet of things. IEEE Internet Things J

  132. Valler NC, Prakash BA, Tong H, Faloutsos M, Faloutsos C (2011) Epidemic spread in mobile ad hoc networks: determining the tipping point. In: International conference on research in networking. Springer, pp 266–280

  133. Van Mieghem P, van de Bovenkamp R (2015) Accuracy criterion for the mean-field approximation in susceptible–infected–susceptible epidemics on networks. Phys Rev E 91(3):032812

    Google Scholar 

  134. Van Mieghem P, Omic J, Kooij R (2008) Virus spread in networks. IEEE/ACM Trans Netw 17(1):1–14

    Google Scholar 

  135. Varanasi A (2021) Covid-19: could game theory help in tackling PPE shortages among health care workers? https://www.forbes.com/sites/anuradhavaranasi/2021/01/31/covid-19-could-game-theory-help-in-tackling-ppe-shortages-among-health-care-workers/?sh=36a76c8594db

  136. Wang J, Wang W, Wang C (2020) Modeling and analysis of conflicting information propagation in a finite time horizon. IEEE/ACM Trans Netw 28(3):972–985

    Google Scholar 

  137. Wang Y, Chakrabarti D, Wang C, Faloutsos C (2003) Epidemic spreading in real networks: An eigenvalue viewpoint. In: 22nd international symposium on reliable distributed systems, 2003. Proceedings. IEEE, pp 25–34

  138. Wang Z, Xia C, Chen Z, Chen G (2020) Epidemic propagation with positive and negative preventive information in multiplex networks. IEEE Trans Cybern 51(1454):1462

    Google Scholar 

  139. Watkins NJ, Nowzari C, Pappas GJ (2019) Robust economic model predictive control of continuous-time epidemic processes. IEEE Trans Autom Control 65(3):1116–1131

    MathSciNet  MATH  Google Scholar 

  140. Watkins NJ, Nowzari C, Preciado VM, Pappas GJ (2016) Optimal resource allocation for competitive spreading processes on bilayer networks. IEEE Trans Control Netw Syst 5(1):298–307

    MathSciNet  MATH  Google Scholar 

  141. Xu Z, Khanafer A, Başar T (2015) Competition over epidemic networks: Nash and Stackelberg games. In: 2015 American control conference (ACC). IEEE, pp 2063–2068

  142. Xue D, Hirche S (2018) Distributed topology manipulation to control epidemic spreading over networks. IEEE Trans Signal Process 67(5):1163–1174

    MathSciNet  MATH  Google Scholar 

  143. Yaesoubi R, Cohen T (2011) Generalized Markov models of infectious disease spread: a novel framework for developing dynamic health policies. Eur J Oper Res 215(3):679–687

    MathSciNet  MATH  Google Scholar 

  144. Yang W (2021) Modeling COVID-19 pandemic with hierarchical quarantine and time delay. Dyn Games Appl 1–23

  145. Zhang HF, Yang Z, Wu ZX, Wang BH, Zhou T (2013) Braess’s paradox in epidemic game: better condition results in less payoff. Sci Rep 3(1):1–8

    Google Scholar 

  146. Zhang L, Xu J (2019) Differential security game in heterogeneous device-to-device offloading network under epidemic risks. IEEE Trans Netw Sci Eng 7(3):1852–1861

    MathSciNet  Google Scholar 

  147. Zhang T, Zhu Q (2021) Informational design of dynamic multi-agent system. arXiv preprint arXiv:2105.03052

  148. Zhao D, Wang L, Wang Z, Xiao G (2018) Virus propagation and patch distribution in multiplex networks: modeling, analysis, and optimal allocation. IEEE Trans Inf Forensics Secur 14(7):1755–1767

    Google Scholar 

  149. Zhu L, Zhou X, Li Y, Zhu Y (2019) Stability and bifurcation analysis on a delayed epidemic model with information-dependent vaccination. Phys Scr 94(12):125202

    Google Scholar 

Download references

Acknowledgements

This work is partially supported by Grants SES-1541164, ECCS-1847056, CNS-2027884, and BCS-2122060 from National Science Foundation (NSF), DOE-NE Grant 20-19829, and Grant W911NF-19-1-0041 from Army Research Office (ARO).

Author information

Authors and Affiliations

  1. New York University, 370 Jay Street, Brooklyn, NY, USA

    Yunhan Huang & Quanyan Zhu

Authors
  1. Yunhan Huang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Quanyan Zhu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yunhan Huang.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This article is part of the topical collection “Modeling and Control of Epidemics” edited by Quanyan Zhu, Elena Gubar and Eitan Altman.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Huang, Y., Zhu, Q. Game-Theoretic Frameworks for Epidemic Spreading and Human Decision-Making: A Review. Dyn Games Appl 12, 7–48 (2022). https://doi.org/10.1007/s13235-022-00428-0

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13235-022-00428-0

Keywords