Herd Behaviors in Epidemics: A Dynamics-Coupled Evolutionary Games Approach

Abstract

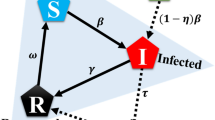
The recent COVID-19 pandemic has led to an increasing interest in the modeling and analysis of infectious diseases. The pandemic has made a significant impact on the way we behave and interact in our daily life. The past year has witnessed a strong interplay between human behaviors and epidemic spreading. In this paper, we propose an evolutionary game-theoretic framework to study the coupled evolution of herd behaviors and epidemics. Our framework extends the classical degree-based mean-field epidemic model over complex networks by coupling it with the evolutionary game dynamics. The statistically equivalent individuals in a population choose their social activity intensities based on the fitness or the payoffs that depend on the state of the epidemics. Meanwhile, the spreading of the infectious disease over the complex network is reciprocally influenced by the players’ social activities. We analyze the coupled dynamics by studying the stationary properties of the epidemic for a given herd behavior and the structural properties of the game for a given epidemic process. The decisions of the herd turn out to be strategic substitutes. We formulate an equivalent finite-player game and an equivalent network to represent the interactions among the finite populations. We develop a structure-preserving approximation technique to study time-dependent properties of the joint evolution of the behavioral and epidemic dynamics. The resemblance between the simulated coupled dynamics and the real COVID-19 statistics in the numerical experiments indicates the predictive power of our framework.

Appendices

Proof of Theorem 1

Proof

Suppose that $\frac{\lambda p (1-s^p_i)}{\gamma }<1$ for all $i\in {\mathcal {I}}^p$ and for all $p\in {\mathcal {P}}$. Since $1-I^p_i(t)\le 1$, we obtain from (4) that: $\frac{\mathrm {d}}{\mathrm {d}t} I^p_i(t)\le -\gamma I^p_i(t)+\lambda (1-s^p_i) p\varTheta (t)$. Then, it suffices to discuss the stability of the system

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t} I(t) = \begin{pmatrix} -\gamma I^1_1(t) \\ \vdots \\ -\gamma I^P_{n^P}(t) \end{pmatrix} +\lambda \begin{pmatrix} 1\cdot (1-s^1_1) \\ \vdots \\ P\cdot (1-s^P_{n^P}) \end{pmatrix} \varTheta (t). \end{aligned}$$

Consider the Lyapunov function $V(t)=\sum _{p\in {\mathcal {P}}} \sum _{i\in {\mathcal {I}}^p} b^p_i I^p_i(t)$, where $b^p_i=\frac{p x^p_i}{\gamma }\ge 0$. The time derivative of the Lyapunov function is:

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}V(t)= & {} -\sum _{p\in {\mathcal {P}}}\sum _{i\in {\mathcal {I}}^p} p x^p_i I^p_i(t)+\sum _{p\in {\mathcal {P}}}\sum _{i\in {\mathcal {I}}^p}\frac{p x^p_i\lambda (1-s^p_i) p\varTheta (t)}{\gamma } \\= & {} -\varTheta (t)\sum _{p\in {\mathcal {P}}}p m^p + \varTheta (t)\sum _{p\in {\mathcal {P}}}\sum _{i\in {\mathcal {I}}^p}\frac{p^2 x^p_i\lambda (1-s^p_i)}{\gamma }\\= & {} \varTheta (t)\sum _{p\in {\mathcal {P}}}\left[ -p m^p+\frac{p^2\lambda }{\gamma }\sum _{i\in {\mathcal {I}}^p}x^p_i(1-s^p_i) \right] . \end{aligned}$$

Combining the assumption that $\frac{\lambda p (1-s^p_i)}{\gamma }<1$ and the condition that $\sum _{i\in {\mathcal {I}}^p}x^p_i=m^p$, we conclude that $\frac{\mathrm {d}}{\mathrm {d}t}V(t)<0$ when $\varTheta (t)\ne 0$. This result shows that the system $\frac{\mathrm {d}}{\mathrm {d}t}I^p_i(t)= -\gamma I^p_i(t)+\lambda (1-s^p_i) p\varTheta (t)$ converges to 0 as $t\rightarrow \infty$. Therefore, the system (4) is globally asymptotically stable at the zero steady state.

Suppose that the opposite condition holds, i.e., $\frac{\lambda p (1-s^p_i)}{\gamma }\ge 1$ for all $i\in {\mathcal {I}}^p$ and for all $p\in {\mathcal {P}}$. We drop the dependence on x of the positive steady-state pair for simplicity. We first show that a solution $\bar{\varTheta }_+\in (0,1]$ exists for (10). Define $\varPsi :[0,1]\rightarrow {\mathbb {R}}$ as: $\varPsi (z)=\sum _{p\in {\mathcal {P}}} \left[ p\sum _{i\in {\mathcal {I}}^p}\frac{x^p_i\theta ^p_i}{\gamma +\theta ^p_iz} \right]$. Since $\varPsi (z)$ is a strictly decreasing function of z, $\varPsi (0)$ achieves the maximum value and $\varPsi (1)$ achieves the minimum value of $\varPsi (\cdot )$. Under the condition $\frac{\lambda p (1-s^p_i)}{\gamma }\ge 1$, we obtain the inequality

$$\begin{aligned} \frac{\theta ^p_i}{\gamma }\ge 1\ge \frac{\theta ^p_i}{\gamma +\theta ^p_i}. \end{aligned}$$

Multiplying by $p x^p_i$ and taking the summation over all $i\in {\mathcal {I}}^p$ and all $p\in {\mathcal {P}}$, we arrive at

$$\begin{aligned} \sum _{p\in {\mathcal {P}}} \left[ p\sum _{i\in {\mathcal {I}}^p}\frac{x^p_i\theta ^p_i}{\gamma } \right] \ge \sum _{p\in {\mathcal {P}}}p m^p \ge \sum _{p\in {\mathcal {P}}} \left[ p\sum _{i\in {\mathcal {I}}^p}\frac{x^p_i\theta ^p_i}{\gamma +\theta ^p_i} \right] , \end{aligned}$$

which is equivalent to $\varPsi (0)\ge \bar{p}\ge \varPsi (1)$. Hence, there exists $\bar{\varTheta }_+\in (0,1]$ such that $\varPsi (\bar{\varTheta }_+)=\bar{p}$. Moreover, $\bar{\varTheta }_+$ is unique because $\varPsi (\cdot )$ is monotone. Accordingly, every element of $\bar{I}_+$ is positive. Now, we proceed to study the stability of the positive steady-state pair $(\bar{I}_+,\bar{\varTheta }_+)$. Define $\phi ^p_i=\frac{\lambda (1-s^p_i)}{\gamma }$. Consider the following equivalent system of (4):

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}I^p_i(t)=-I^p_i(t)+\phi ^p_i p(1-I^p_i(t))\varTheta (t). \end{aligned}$$

Let the density of the susceptible be $U^p_i(t)=1-I^p_i(t)$, (5) can be rewritten as

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}\varTheta (t)= & {} \bar{p}^{-1}\sum _{p\in {\mathcal {P}}}\sum _{i\in {\mathcal {I}}^p} p x^p_i\frac{\mathrm {d}}{\mathrm {d}t} I^p_i(t)\\= & {} \bar{p}^{-1}\sum _{p\in {\mathcal {P}}}\sum _{i\in {\mathcal {I}}^p} p x^p_i\left[ -I^p_i(t) + \phi ^p_i p U^p_i(t) \varTheta (t) \right] \\= & {} \varTheta (t)\left[ \bar{p}^{-1}\sum _{p\in {\mathcal {P}}}\sum _{i\in {\mathcal {I}}^p}\phi ^p_i U^p_i(t) p^2 x^p_i-1 \right] . \end{aligned}$$

Consider the following Lyapunov function for the equivalent dynamical systems above: $V(t)=\frac{1}{2}\sum _{p\in {\mathcal {P}}}\sum _{i\in {\mathcal {I}}^p}\left[ b^p_i (U^p_i(t)-\bar{U}^p_i)^2 \right] +\varTheta (t)-\bar{\varTheta }-\bar{\varTheta }ln\frac{\varTheta (t)}{\bar{\varTheta }}$, where the parameters $b^p_i$ are defined as $b^p_i=\frac{p x^p_i}{\bar{p} \bar{U}^p_i}$, and the term $\bar{U}^p_i$ denotes the steady-state quantity of $U^p_i(t)$. The time derivative of V(t) is

$$\begin{aligned} \begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}V(t)&= \sum _{p\in {\mathcal {P}}}\sum _{i\in {\mathcal {I}}^p} b^p_i (U^p_i(t)-\bar{U}^p_i)\frac{\mathrm {d}U^p_i(t)}{\mathrm {d}t} + \frac{\varTheta (t)-\bar{\varTheta }}{\varTheta (t)}\cdot \frac{\mathrm {d}\varTheta (t)}{\mathrm {d}t} \\&=\sum _{p\in {\mathcal {P}}}\sum _{i\in {\mathcal {I}}^p} b^p_i (U^p_i(t)-\bar{U}^p_i)(I^p_i(t) - \phi ^p_i p U^p_i(t)\varTheta (t)) \\&\qquad +(\varTheta (t)-\bar{\varTheta })\left[ \frac{\sum _{p\in {\mathcal {P}}}\sum _{i\in {\mathcal {I}}^p} \phi ^p_i U^p_i(t) p^2 x^p_i}{\bar{p}}-1 \right] . \end{aligned} \end{aligned}$$

Since $\bar{U}^p_i=1-\bar{I}^p_i$ and $\bar{p}^{-1}\sum _{p\in {\mathcal {P}}}\sum _{i\in {\mathcal {I}}^p} p^2 x^p_i \phi ^p_i \bar{U}^p_i=1$, we obtain

$$\begin{aligned} \begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}V(t)&= \sum _{p\in {\mathcal {P}}}\sum _{i\in {\mathcal {I}}^p} b^p_i (U^p_i(t)-\bar{U}^p_i)\left[ (I^p_i(t)-\bar{I}^p_i) - \phi ^p_i p(U^p_i(t)-\bar{U}^p_i) \right] \\&\qquad +(\varTheta (t)-\bar{\varTheta })\left[ \bar{p}^{-1}\sum _{p\in {\mathcal {P}}}\sum _{i\in {\mathcal {I}}^p} \phi ^p_i p^2 x^p_i (U^p_i(t)-\bar{U}^p_i) \right] \\&= \sum _{p\in {\mathcal {P}}}\sum _{i\in {\mathcal {I}}^p} b^p_i \left[ (U^p_i(t)-\bar{U}^p_i)(I^p_i(t)-\bar{I}^p_i)\right] \\&\qquad + \bar{p}^{-1} \sum _{p\in {\mathcal {P}}} \sum _{i\in {\mathcal {I}}^p} \frac{\phi ^p_i p^2 x^p_i}{\bar{U}^p_i}(U^p_i(t)-\bar{U}^p_i)\left[ U^p_i(t)\varTheta (t) -\bar{U}^p_i\bar{\varTheta }\right] \\&\qquad + \bar{p}^{-1}\sum _{p\in {\mathcal {P}}}\sum _{i\in {\mathcal {I}}^p} \phi ^p_i p^2 x^p_i \left[ (\varTheta (t)-\bar{\varTheta })(U^p_i(t)-\bar{U}^p_i) \right] \\&= -\sum _{p\in {\mathcal {P}}}\sum _{i\in {\mathcal {I}}^p} b^p_i (U^p_i(t)-\bar{U}^p_i)^2\\&\qquad - \bar{p}^{-1}\sum _{p\in {\mathcal {P}}}\sum _{i\in {\mathcal {I}}^p} \phi ^p_i p^2 x^p_i \varTheta (t)\left[ \frac{(U^p_i(t))^2}{\bar{U}^p_i}-2U^p_i(t)+\bar{U}^p_i \right] . \end{aligned} \end{aligned}$$

Since $\forall U^p_i(t)\in [0,1]$, $\frac{(U^p_i(t))^2}{\bar{U}^p_i}-2U^p_i(t)+\bar{U}^p_i\ge 0$, we conclude that $\frac{\mathrm {d}}{\mathrm {d}t}V(t)\le 0$. Therefore, the positive steady-state pair $(\bar{I}_+,\bar{\varTheta }_+)$ is globally asymptotically stable. $\square$

Proof of Theorem 2

Proof

Consider the component $\frac{x^p_i\theta ^p_iz}{\gamma +x^p_i\theta ^p_iz}$. For arbitrary $z_1,z_2\in [0,1]$, the following holds:

$$\begin{aligned} \begin{aligned}&\left| \frac{x^p_i\theta ^p_iz_1}{\gamma +x^p_i\theta ^p_iz_1} -\frac{x^p_i\theta ^p_iz_2}{\gamma +x^p_i\theta ^p_iz_2} \right| \\&\quad =x^p_i\theta ^p_i \left| \frac{\gamma (z_1-z_2)}{(\gamma +x^p_i\theta ^p_iz_1)(\gamma +x^p_i\theta ^p_iz_2)} \right| \\&\quad = x^p_i\theta ^p_i \beta ^p_i \left| z_1-z_2 \right| , \end{aligned} \end{aligned}$$

where $\beta ^p_i=\frac{1}{(1+\gamma ^{-1} x^p_i \theta ^p_i z_1)(1+\gamma ^{-1}x^p_i\theta ^p_i z_2)}<1$. Then, summing all components, we obtain

$$\begin{aligned} \left| M(z_1)-M(z_2) \right| = \frac{|z_1-z_2|}{\bar{p}} \left( \sum _{p\in {\mathcal {P}}}\sum _{i\in {\mathcal {I}}^p} p x^p_i\theta ^p_i \beta ^p_i \right) . \end{aligned}$$

Since $\bar{p} = \sum _{p\in {\mathcal {P}}}p m^p$, $m^p = \sum _{i\in {\mathcal {I}}^p} x^p_i$, $\theta ^p_i\in [0,1]$, and $\beta ^p_i \in (0,1)$, we conclude that $\bar{p}^{-1}(\sum _{p\in {\mathcal {P}}}\sum _{i\in {\mathcal {I}}^p} p x^p_i\theta ^p_i \beta ^p_i)\in (0,1)$. Therefore, $M(\cdot )$ is a contraction mapping on [0, 1].

$\square$

Proof of Theorem 3

Proof

The constraint $-F^p(x)\ge -y^p{\mathbf {1}}_{n^p}$ leads to

$$\begin{aligned} -EF^p(x) = -(x^p)^{\mathsf {T}}F^p(x) \ge -(x^p)^{\mathsf {T}}y^p{\mathbf {1}}_{n^p}\ge -y^p m^p. \end{aligned}$$

This implies that the objective function is nonnegative, i.e.,

$$\begin{aligned} \sum _{p\in {\mathcal {P}}}-EF^p(x)+\sum _{p\in {\mathcal {P}}}y^p m^p \ge 0. \end{aligned}$$

Suppose that $x^*=(x^{1*},...,x^{P*})$ is an NE of the population game. Define $y^*=(y^{1*},...,y^{P*})$ by $y^{p*}=(m^p)^{-1}EF^p(x^{p*},x^{-p*})$ for all $p\in {\mathcal {P}}$. We prove that the pair $(x^*,y^*)$ is an optimal solution to problem (12) by showing that it is feasible and $\sum _{p\in {\mathcal {P}}}-EF^p(x^*) + \sum _{p\in {\mathcal {P}}}y^{p*} m^p=0$. To prove the feasibility of $(x^*, y^*)$, it suffices to prove $-F^p(x^*)\ge -y^{p*}{\mathbf {1}}_{n^p}$ for all $p \in {\mathcal {P}}$. Since

$$\begin{aligned} y^{p*}=(m^p)^{-1}(x^{p*})^{\mathsf {T}}F^p(x^{p*},x^{-p*}), \end{aligned}$$

we obtain

$$\begin{aligned} -y^{p*}{\mathbf {1}}_{n^p}=-(m^p)^{-1}(x^{p*})^{\mathsf {T}}F^p(x^{p*},x^{-p*}){\mathbf {1}}_{n^p}. \end{aligned}$$

Then, it suffices to prove

$$\begin{aligned} -(x^{p*})^{\mathsf {T}}F^p(x^{p*},x^{-p*}){\mathbf {1}}_{n^p}\le -m^p\begin{pmatrix} ({\mathbf {e}}^p_1)^{\mathsf {T}}F^p(x^{p*},x^{-p*}) \\ \vdots \\ ({\mathbf {e}}^p_{n^p})^{\mathsf {T}}F^p(x^{p*},x^{-p*}) \\ \end{pmatrix}, \end{aligned}$$

(36)

where ${\mathbf {e}}^p_i \in {\mathbb {R}}^{n^p}$ is the vector of all zeros except for a 1 at the ith entry for population $p \in {\mathcal {P}}$. From Definition 1, we know that if $x^{p*}_i>0$, $s^p_i\in \arg {\text {max}}_{j\in {\mathcal {I}}^p}F^p_j(x^*)$. This shows that for all $i\in {\mathcal {I}}^p$ such that $x^{p*}_i>0$, the values of $F^p_i(x^{p*},x^{-p*})$ are all equivalent to ${\text {max}}_{j\in {\mathcal {I}}^p}F^p_j(x^*)$. Then, for all i such that $x^{p*}_i>0$, since ${\mathbf {1}}^{\mathsf {T}}x^{p*}=m^p$, equality holds in the ith row of (36). For $j\in {\mathcal {I}}^p$ such that $x^{p*}_j=0$, inequality holds in the jth row of (36) since $F^p_j(x^*)\le \arg {\text {max}}_{i\in {\mathcal {I}}^p}F^p_i(x^*)$. Hence, the pair $(x^*,y^*)$ is feasible. From the definition of $y^*$, we conclude that the objective function is zero under $(x^*,y^*)$. Therefore, $(x^*,y^*)$ solves (12).

Suppose that $\tilde{x}=(\tilde{x}^1,...,\tilde{x}^P)$ and $\tilde{y}=(\tilde{y}^1,...,\tilde{y}^P)$ solve (12). Since we have found the pair $(x^*,y^*)$ under which the objective value is zero, the objective value must be zero under the pair $(\tilde{x},\tilde{y})$, i.e., $\sum _{p\in {\mathcal {P}}}-EF^p(\tilde{x}^p,\tilde{x}^{-p})+\sum _{p\in {\mathcal {P}}}\tilde{y}^p m^p=0$. For all x such that $x\ge 0$ and ${\mathbf {1}}^{\mathsf {T}}x^p=m^p, \forall p\in {\mathcal {P}}$, $-(x^p)^{\mathsf {T}}F^p(\tilde{x})\ge -\tilde{y}^p m^p$ holds. This leads to

$$\begin{aligned} \begin{aligned} \sum _{p\in {\mathcal {P}}}-(x^p)^{\mathsf {T}}F^p(\tilde{x}) \ge&\sum _{p\in {\mathcal {P}}}-\tilde{y}^p m^p =\sum _{p\in {\mathcal {P}}}-EF^p(\tilde{x}^p,\tilde{x}^{-p})\\ =&\sum _{p\in {\mathcal {P}}} -(\tilde{x^p})^{\mathsf {T}}F^p(\tilde{x}). \end{aligned} \end{aligned}$$

Since $\forall p\in {\mathcal {P}}$, $-(\tilde{x}^p)^{\mathsf {T}}F^p(\tilde{x})\ge -\tilde{y}^p m^p$ holds. Hence, $\forall p\in {\mathcal {P}}$, $-(\tilde{x}^p)^{\mathsf {T}}F^p(\tilde{x})=-\tilde{y}^p m^p$. Therefore, $\forall p\in {\mathcal {P}}$ and $\forall x^p$ feasible, we obtain

$$\begin{aligned} -(\tilde{x}^p)^{\mathsf {T}}F^p(\tilde{x})\le -(x^p)^{\mathsf {T}}F^p(\tilde{x}). \end{aligned}$$

(37)

Setting $x^p = m^p {\mathbf {e}}^p_1$, $x^p = m^p {\mathbf {e}}^p_2$, up to $x^p = m^p {\mathbf {e}}^p_{n^p}$ in (37), we arrive at

$$\begin{aligned} (\tilde{x}^p)^{\mathsf {T}}F^p(\tilde{x}) \ge \left( {\text {max}}_{i\in {\mathcal {I}}^p} F^p_i(\tilde{x}) \right) m^p. \end{aligned}$$

(38)

Since $\tilde{x} \ge 0$ and ${\mathbf {1}}^{\mathsf {T}}\tilde{x}^p = m^p$, equality holds in (38). Thus, we conclude that for $i\in {\mathcal {I}}^p$ such that $\tilde{x}^p_i>0$, $i\in \arg {\text {max}}_{i\in {\mathcal {I}}^p}F^p_i(\tilde{x})$. Therefore, $\tilde{x}$ is an NE of the population game, which completes the proof. $\square$