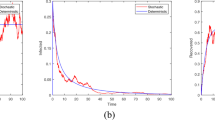
Abstract
Rumor is an important form of social interaction, and its spreading has a significant impact on human lives. The optimal control theory is an important tool to better manage the spread of rumors. Most of the literature on rumor propagation models deals with quadratic cost functions relative to the control variable. In this paper, we have considered a time-delay rumor propagation model with saturated control functions and an objective function of \(L^1\)-type linear with respect to the control variables. In the general case, the introduction of the delay in the dynamic systems represents the time lag between the action on the system and the response of the system to this action. The delay is incorporated in our model to make it more realistic and to describe the latency period. The existence of the optimal control pair is also proved. Pontryagin’s maximum principle with delay is used to characterize these optimal controls. The optimality system is derived and then solved numerically using an algorithm based on the forward and backward difference approximation.






Similar content being viewed by others
References
Bettencourt LMA, Cintrón-Arias A, Kaiser DI, Castillo-Chávez C (2006) The power of a good idea: quantitative modeling of the spread of ideas from epidemiological models. Physica A 364:513–536
Brezis H, Ciarlet PG, Lions JL (1999) Analyse fonctionnelle: théorie et applications. Dunod Paris vol 91, Malakoff
Buzna L, Peters K, Helbing D (2006) Modelling the dynamics of disaster spreading in networks. Physica A 363(1):132–140
Daley DJ, Kendall DG (1964) Epidemics and rumours. Nature 204:1118
Göllmann L, Kern D, Maurer H (2009) Optimal control problems with delays in state and control variables subject to mixed control-state constraints. Optimal Control Appl Methods 30(4):341–365
Hale JK, Lunel SMV (2013) Introduction to functional differential equations, vol 99. Springer, New York
Hassan Laarabi H, Labriji E, Rachik M, Kaddar A (2012) Optimal control of an epidemic model with a saturated incidence rate. Nonlinear Anal Model Control 17(4):448–459
Hattaf K, Yousfi N (2012) Optimal control of a delayed HIV infection model with immune response using an efficient numerical method. ISRN Biomathematics. https://doi.org/10.5402/2012/215124
Huang W (2011) On rumour spreading with skepticism and denial. Technical Report
Huo LA, Ma C (2018) Optimal control of rumor spreading model with consideration of psychological factors and time delay. Discrete Dyn Nat Soc 2018:9314907
Kandhway K, Kuri J (2014a) How to run a campaign: optimal control of SIS and SIR information epidemics. Appl Math Comput 231:79–92
Kandhway K, Kuri J (2014b) Optimal control of information epidemics modeled as Maki Thompson rumors. Commun Nonlinear Sci Numer Simul 19(12):4135–4147
Kosfeld M (2005) Rumours and markets. J Math Econ 41:646–66
Laarabi H, Abta A, Rachik M, Bouyaghroumni J (2016) Stability analysis of a delayed rumor propagation model. Differ Equ Dyn Syst 24:407–415
Li C (2017) A study on time-delay rumor propagation model with saturated control function. Adv Differ Equ 1:255
Lin T, Fan C, Liu C, Zhao J (2015) Optimal control of a rumor propagation model with latent period in emergency event. Adv Differ Equ 2015(1):54
Maki D, Thomson M (1973) Mathematical models and applications. Prentice-Hall, Englewood Cliffs
Nekovee M, Moreno Y, Bianconi G, Marsili M (2007) Theory of rumour spreading in complex social networks. Physica A 374:457
Wang YQ, Yang XY, Wang J (2014) A rumor spreading model with control mechanism on social networks. Chin J Phys 52:816
Zhou L, Fan M (2012) Dynamics of an SIR epidemic model with limited medical resources revisited. Nonlinear Anal Real World Appl 13:312–324
Acknowledgements
The authors thank the editor and the anonymous referees for very helpful suggestions and comments that helped us to improve the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Abta, A., Laarabi, H., Rachik, M. et al. Optimal control of a delayed rumor propagation model with saturated control functions and \(L^1\)-type objectives. Soc. Netw. Anal. Min. 10, 73 (2020). https://doi.org/10.1007/s13278-020-00685-0
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13278-020-00685-0