Skip to main content
Springer Nature Link
Log in

Convergence of batch gradient algorithm with smoothing composition of group \(l_{0}\) and \(l_{1/2}\) regularization for feedforward neural networks

  • Regular Paper
  • Published:
Progress in Artificial Intelligence Aims and scope Submit manuscript

Abstract

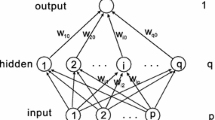
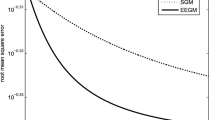
In this paper, we prove the convergence of batch gradient method for training feedforward neural network; we have proposed a new penalty term based on composition of smoothing \(L_{1/2}\) penalty for weights vectors incoming to hidden nodes and smoothing group \(L_{0}\) regularization for the resulting vector (BGSGL\(_{0}\)L\(_{1/2}\)). This procedure forces weights to become smaller in group level, after training, which allow to remove some redundant hidden nodes. Moreover, it can remove some redundant weights of the surviving hidden nodes. The conditions of convergence are given. The importance of our proposed regularization objective is also tested on numerical examples of classification and regression task.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Hornik, K., Stinchcombe, M., White, H.: Multilayer feedforward networks are universal approximators. Neural Netw. 2(5), 359–366 (1989)

    Article  Google Scholar 

  2. Rumelhart, D.E., Hinton, G.E., Williams, R.J.: Learning representations by back-propagating errors. Nature 323(6088), 533 (1986)

    Article  Google Scholar 

  3. Nakama, T.: Theoretical analysis of batch and on-line training for gradient descent learning in neural networks. Neurocomputing 73(1–3), 151–159 (2009)

    Article  Google Scholar 

  4. Wang, J., Yang, G., Liu, S., Zurada, J.M.: Convergence analysis of multilayer feedforward networks trained with penalty terms: a review. J. Appl. Comput. Sci. Methods 7(2), 89–103 (2015)

    Article  Google Scholar 

  5. Wang, J., Xu, C., Yang, X., Zurada, J.M.: A novel pruning algorithm for smoothing feedforward neural networks based on group lasso method. IEEE Trans. Neural Netw. Learn. Syst. 29(5), 2012–2024 (2018)

    Article  MathSciNet  Google Scholar 

  6. Li, F., Zurada, J.M., Wu, W.: Smooth group \(l_{1/2}\) regularization for input layer of feedforward neural networks. Neurocomputing 314, 109–119 (2018)

  7. Zhang, H., Tang, Y., Liu, X.: Batch gradient training method with smoothing \(l_{0}\) regularization for feedforward neural networks. Neural Comput. Appl. 26(2), 383–390 (2015)

  8. Wu, W., Feng, G., Li, Z., Xu, Y.: Deterministic convergence of an online gradient method for bp neural networks. IEEE Trans. Neural Netw. 16(3), 533–540 (2005)

    Article  Google Scholar 

  9. Reed, R.: Pruning algorithms—a survey. IEEE Trans. Neural Netw. 4(5), 740–747 (1993)

    Article  Google Scholar 

  10. Gethsiyal Augasta, M., Kathirvalavakumar, T.: A novel pruning algorithm for optimizing feedforward neural network of classification problems. Neural Process. Lett. 34(3), 241 (2011)

    Article  Google Scholar 

  11. MacKay, D.J.C.: The evidence framework applied to classification networks. Neural Comput. 4(5), 720–736 (1992)

    Article  Google Scholar 

  12. Ramchoun, H., Ettaouil, M.: Hamiltonian monte carlo based on evidence framework for bayesian learning to neural network. Soft Comput. pp. 1–11, (2018)

  13. Tibshirani, Robert.: Regression shrinkage and selection via the lasso. J. Royal Stat. Soc. Series B (Methodol), pp. 267–288, (1996)

  14. Setiono, R.: A penalty-function approach for pruning feedforward neural networks. Neural Comput. 9(1), 185–204 (1997)

    Article  Google Scholar 

  15. Loone, S., Irwin, G.: Improving neural network training solutions using regularisation. Neurocomputing 37(1–4), 71–90 (2001)

    Article  Google Scholar 

  16. Wu, W., Shao, H., Li, Z.: Convergence of batch bp algorithm with penalty for fnn training. In International Conference on Neural Information Processing, pp. 562–569. Springer, (2006)

  17. Zhang, H., Wu, W., Yao, M.: Boundedness of a batch gradient method with penalty for feedforward neural networks. In Proceedings of the 12th WSEAS International Conference on Applied Mathematics, pp. 175–178. Citeseer, (2007)

  18. Zhang, H., Wu, W., Yao, M.: Boundedness and convergence of batch back-propagation algorithm with penalty for feedforward neural networks. Neurocomputing 89, 141–146 (2012)

    Article  Google Scholar 

  19. Wu, W., Fan, Q., Zurada, J.M., Wang, J., Yang, D., Liu, Y.: Batch gradient method with smoothing l1/2 regularization for training of feedforward neural networks. Neural Netw. 50, 72–78 (2014)

    Article  Google Scholar 

  20. Fan, Q., Wu, W., Zurada, J.M.: Convergence of batch gradient learning with smoothing regularization and adaptive momentum for neural networks. SpringerPlus 5(1), 295 (2016)

    Article  Google Scholar 

  21. Simon, N., Friedman, J., Hastie, T., Tibshirani, R.: A sparse-group lasso. J. Comput. Graph. Stat. 22(2), 231–245 (2013)

    Article  MathSciNet  Google Scholar 

  22. Scardapane, S., Comminiello, D., Hussain, A., Uncini, A.: Group sparse regularization for deep neural networks. Neurocomputing 241, 81–89 (2017)

    Article  Google Scholar 

  23. Wang, J., Cai, Q., Chang, Q., Zurada, J.M.: Convergence analyses on sparse feedforward neural networks via group lasso regularization. Inf. Sci. 381, 250–269 (2017)

    Article  MathSciNet  Google Scholar 

  24. Zhang, H., Tang, Y.: Online gradient method with smoothing \(l_{0}\) regularization for feedforward neural networks. Neurocomputing 224, 1–8 (2017)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Laboratory of Mathematical Modeling, Simulation and Smart Systems, National School of Business and Management, University of Moulay Ismail, Meknes, Morocco

    Hassan Ramchoun

  2. Department of Mathematics and Informatics, Faculty of Sciences and Techniques, USMBA, Fes, Morocco

    Mohamed Ettaouil

Authors
  1. Hassan Ramchoun
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Mohamed Ettaouil
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Hassan Ramchoun.

Ethics declarations

Conflict of interest

The authors declare that they have no conflicts of interest.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ramchoun, H., Ettaouil, M. Convergence of batch gradient algorithm with smoothing composition of group \(l_{0}\) and \(l_{1/2}\) regularization for feedforward neural networks. Prog Artif Intell 11, 269–278 (2022). https://doi.org/10.1007/s13748-022-00285-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13748-022-00285-3

Keywords