Summary.
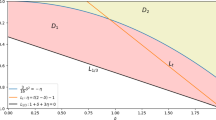
In this paper we illustrate a novel approach for studying the asymptotic behaviour of the solutions of linear difference equations with variable coefficients. In particular, we deal with the zero-stability of the 3-step BDF-method on grids with variable stepsize for the numerical solution of IVPs for ODEs. Our approach is based on the theory of the spectral radius of a family of matrices and yields almost optimal results, which give a slight improvement to the best results already known from the literature. The success got on the chosen example suggests that our approach has a good potential for more general and harder stability analyses of numerical methods.
Similar content being viewed by others
Author information
Authors and Affiliations
Additional information
Received May 19, 1999 / Revised version received February 21, 2000 / Published online November 8, 2000
Rights and permissions
About this article
Cite this article
Guglielmi, N., Zennaro, M. On the zero-stability of variable stepsize multistep methods: the spectral radius approach. Numer. Math. 88, 445–458 (2001). https://doi.org/10.1007/s211-001-8010-0
Issue Date:
DOI: https://doi.org/10.1007/s211-001-8010-0