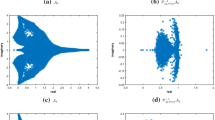
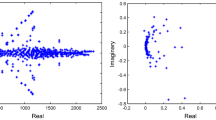
Abstract
In this paper, a class of new preconditioners based on matrix splitting are presented for generalized saddle-point linear systems, which improve some recently published preconditioners in view of spectral distributions and numerical performances. Moreover, we widen the scope of the new preconditioners to solve more general but rarely considered saddle-point linear systems with singular leading blocks and rank-deficient off-diagonal blocks. The new variants can result in much better convergence properties and spectrum distributions than the original existing preconditioners. Numerical experiments are given to illustrate the efficiency of the new proposed preconditioners.





Similar content being viewed by others
References
Axelsson O (2015) Unified analysis of preconditioning methods for saddle point matrices. Numer Linear Algebra Appl 22(2):233–253
Bai Z-Z (2012) Block alternating splitting implicit iteration methods for saddle-point problems from time-harmonic eddy current models. Numer Linear Algebra Appl 19:914–936
Bai Z-Z (2018a) On spectral clustering of HSS preconditioner for generalized saddle-point matrices. Linear Algebra Appl 555:285–300
Bai Z-Z (2018b) Regularized HSS iteration methods for stabilized saddle-point problems. IMA J Numer Anal. https://doi.org/10.1093/imanum/dry046
Bai Z-Z, Benzi M (2017) Regularized HSS iteration methods for saddle-point linear systems. BIT Numer Math 57(2):287–311
Bai Z-Z, Golub GH (2007) Accelerated Hermitian and skew-Hermitian splitting iteration methods for saddle-point problems. IMA J Numer Anal 27(1):1–23
Bai Z-Z, Hadjidimos A (2014) Optimization of extrapolated Cayley transform with non-Hermitian positive definite matrix. Linear Algebra Appl 463:322–339
Bai Z-Z, Golub GH, Ng MK (2003) Hermitian and skew-Hermitian splitting methods for non-Hermitian positive definite linear systems. SIAM J Matrix Anal Appl 24(3):603–626
Bai Z-Z, Golub GH, Pan J-Y (2004) Preconditioned Hermitian and skew-Hermitian splitting methods for non-Hermitian positive semidefinite linear systems. Numer Math 98(1):1–32
Bai Z-Z, Golub GH, Lu L-Z, Yin J-F (2005) Block triangular and skew-Hermitian splitting methods for positive-definite linear systems. SIAM J Sci Comput 26(3):844–863
Bai Z-Z, Ng MK, Wang Z-Q (2009) Constraint preconditioners for symmetric indefinite matrices. SIAM J Matrix Anal Appl 31(2):410–433
Beik FPA, Benzi M, Chaparpordi SHA (2017) On block diagonal and block triangular iterative schemes and preconditioners for stabilized saddle point problems. J Comput Appl Math 326:15–30
Benzi M, Golub GH (2004) A preconditioner for generalized saddle point problems. SIAM J Matrix Anal Appl 26(1):20–41
Benzi M, Olshanskii MA (2006) An augmented Lagrangian-based approach to the Ossen problem. SIAM J Sci Comput 28:2095–2113
Benzi M, Simoncini V (2006) On the eigenvalues of a class of saddle point matrices. Numer Math 103(2):173–196
Benzi M, Wang Z (2011) Analysis of augmented Lagrangian-based preconditioners for the steady incompressible Navier–Stokes equations. SIAM J Sci Comput 33:2761–2784
Benzi M, Golub GH, Liesen J (2005) Numerical solution of saddle point problems. Acta Numer 14:1–137
Benzi M, Olshanskii MA, Wang Z (2011) Modified augmented Lagrangian preconditioners for the incompressible Navier–Stokes equations. Int J Numer Methods Fluids 66:486–508
Cao Y, Dong J-L, Wang Y-M (2015) A relaxed deteriorated PSS preconditioner for nonsymmetric saddle point problems from the steady Navier–Stokes equation. J Comput Appl Math 273:41–60
Chaparpordi SHA, Beik FPA, Salkuyeh DK (2018) Block triangular preconditioners for stabilized saddle point problems with nonsymmetric (1, 1)-block. Comput Math Appl 76:1544–1553
Dollar HS (2007) Constraint-style preconditioners for regularized saddle point problems. SIAM J Matrix Anal Appl 29(2):672–684
Elman HC (1999) Preconditioning for the steady-state Navier–Stokes equations with low viscosity. SIAM J Sci Comput 20(4):1299–1316
Elman HC, Ramage A, Silvester DJ (2007) Algorithm 866: IFISS, a Matlab toolbox for modelling incompressible flow. ACM Trans Math Softw 33(2):14
Golub GH, Greif C (2003) On solving block-structured indefinite linear systems. SIAM J Sci Comput 24:2076–2092
Hezari D, Edalatpour V (2019) On the generalized deteriorated positive semi-definite and skew-Hermitian splitting preconditioner. J Comput Math 37:18–32
Huang T-Z, Wu S-L, Li C-X (2009) The spectral properties of the Hermitian and skew-Hermitian splitting preconditioner for generalized saddle point problems. J Comput Appl Math 229(1):37–46
Keller C, Gould NI, Wathen AJ (2000) Constraint preconditioning for indefinite linear systems. SIAM J Matrix Anal Appl 21(4):1300–1317
Klawonn A (1998) Block-triangular preconditioners for saddle point problems with a penalty term. SIAM J Sci Comput 19(1):172–184
Liang Z-Z, Zhang G-F (2016) Two new variants of the HSS preconditioner for regularized saddle point problems. Comput Math Appl 72:603–619
Liang Z-Z, Zhang G-F (2018) Variants of the deteriorated PSS preconditioner for saddle point problems. Comput Math Appl 75:3024–3046
Murphy MF, Golub GH, Wathen AJ (2000) A note on preconditioning for indefinite linear systems. SIAM J Sci Comput 21(6):1969–1972
Notay Y (2014) A new analysis of block preconditioners for saddle point problems. SIAM J Matrix Anal Appl 35(1):143–173
Pan J-Y, Ng MK, Bai Z-Z (2006) New preconditioners for saddle point problems. Appl Math Comput 172(2):762–771
Rehman M, Vuik C, Segal G (2009) SIMPLE-type preconditioners for the Oseen problem. Int J Numer Methods Fluids 61:432–452
Rozlnoník M, Simoncini V (2002) Krylov subspace methods for saddle point problems with indefinite preconditioning. SIAM J Matrix Anal Appl 24(2):368–391
Saad Y (2003) Iterative methods for sparse linear systems. SIAM, Philadelphia
Shen Q-Q, Cao Y, Wang L (2017) Two improvements of the deteriorated PSS preconditioner for generalized saddle point problems. Numer Algorithms 75(1):33–54
Shen S-Q (2014) A note on PSS preconditioners for generalized saddle point problems. Appl Math Comput 237:723–729
Shen S-Q, Huang T-Z, Yu J (2010) Eigenvalue estimates for preconditioned nonsymmetric saddle point matrices. SIAM J Matrix Anal Appl 31(5):2453–2476
Simoncin V, Benzi M (2004) Specrtal properities of the Hermitian and skew-Hermitian splitting preconditioner for saddle point problems. SIAM J Matrix Anal Appl 26(2):377–389
Simoncini V (2004) Block triangular preconditioners for symmetric saddle-point problems. Appl Numer Math 49(1):63–80
Wathen AJ (2015) Preconditioning. Acta Numer 24:329–376
Acknowledgements
We would like to express our sincere thanks to the two unknown reviewers for their careful reading of the manuscript. Their useful comments and valuable suggestions greatly improve the quality of the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Ernesto G. Birgin.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by the National Natural Science Foundation of China (Nos. 11801242 and 11771193) and the Fundamental Research Funds for the Central Universities (No. lzujbky-2018-31).
Rights and permissions
About this article
Cite this article
Liang, ZZ., Zhang, GF. A class of modified DPSS preconditioners for generalized saddle-point linear systems. Comp. Appl. Math. 38, 84 (2019). https://doi.org/10.1007/s40314-019-0844-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40314-019-0844-2