Skip to main content
Springer Nature Link
Log in

Barycentric rational collocation methods for Volterra integral equations with weakly singular kernels

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

Abstract

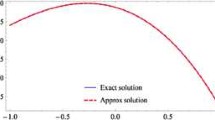
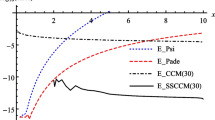
In this paper, we investigate barycentric rational collocation methods for weakly singular Volterra integral equations. Since the exact solution usually has a weak singularity at the initial point, a smoothing transformation is first used to convert the original equation to a new equation whose exact solution is smooth enough. Then, by the collocation approach based on barycentric rational interpolation, a discrete numerical scheme is constructed, and a general convergence result is established. Finally, the theoretical results are illustrated by some numerical examples.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Abdi A, Berrut JP, Hosseini SA (2018) The linear barycentric rational method for a class of delay Volterra integro-differential equations. J Sci Comput 75(3):1757–1775

    Article  MathSciNet  MATH  Google Scholar 

  • Berrut JP, Hosseini SA, Klein G (2014) The linear barycentric rational quadrature method for Volterra integral equations. SIAM J Sci Comput 36(1):A105–A123

    Article  MathSciNet  MATH  Google Scholar 

  • Brunner H (1983) Nonpolynomial spline collocation for Volterra equations with weakly singular kernels. SIAM J Numer Anal 20(6):1106–1119

    Article  MathSciNet  MATH  Google Scholar 

  • Brunner H (1985) The numerical solution of weakly singular Volterra integral equations by collocation on graded meshes. Math. Comput. 45(172):417–437

    Article  MathSciNet  MATH  Google Scholar 

  • Brunner H (2004) Collocation methods for Volterra integral and related functional differential equations, vol 15. Cambridge University Press, Cambridge

    Book  MATH  Google Scholar 

  • Brunner H, van der Houwen PJ (1986) The numerical solution of Volterra equations, vol 3. Elsevier Science Ltd, Amsterdam

    MATH  Google Scholar 

  • Cameron R, McKee S (1984) Product integration methods for second-kind Abel integral equations. J Comput Appl Math 11(1):1–10

    Article  MathSciNet  MATH  Google Scholar 

  • Cao Y, Herdman T, Xu Y (2003) A hybrid collocation method for Volterra integral equations with weakly singular kernels. SIAM J Numer Anal 41(1):364–381

    Article  MathSciNet  MATH  Google Scholar 

  • Chen Y, Tang T (2010) Convergence analysis of the Jacobi spectral-collocation methods for Volterra integral equations with a weakly singular kernel. Math Comput 79(269):147–167

    Article  MathSciNet  MATH  Google Scholar 

  • de Hoog F, Weiss R (1974) High order methods for a class of Volterra integral equations with weakly singular kernels. SIAM J Numer Anal 11(6):1166–1180

    Article  MathSciNet  MATH  Google Scholar 

  • Diogo T, McKee S, Tang T (1994) Collocation methods for second-kind Volterra integral equations with weakly singular kernels. Proc R Soc Edinb Sect A 124(2):199–210

    Article  MathSciNet  MATH  Google Scholar 

  • Dragomir SS (2003) Some Gronwall type inequalities and applications. Nova Science Publishers Inc, Hauppauge

    MATH  Google Scholar 

  • Floater MS, Hormann K (2007) Barycentric rational interpolation with no poles and high rates of approximation. Numer Math 107(2):315–331

    Article  MathSciNet  MATH  Google Scholar 

  • Gu Z, Guo X, Sun D (2016) Series expansion method for weakly singular Volterra integral equations. Appl Numer Math 105:112–123

    Article  MathSciNet  MATH  Google Scholar 

  • Guan Q, Zhang R, Zou Y (2012) Analysis of collocation solutions for nonstandard Volterra integral equations. IMA J Numer Anal 32(4):1755–1785

    Article  MathSciNet  MATH  Google Scholar 

  • Hu Q (1997) Superconvergence of numerical solutions to Volterra integral equations with singularities. SIAM J Numer Anal 34(5):1698–1707

    Article  MathSciNet  MATH  Google Scholar 

  • Li M, Huang C (2019) The linear barycentric rational quadrature method for auto-convolution Volterra integral equations. J Sci Comput 78(1):549–564

    Article  MathSciNet  MATH  Google Scholar 

  • Liang H, Stynes M (2018) Collocation methods for general Caputo two-point boundary value problems. J Sci Comput 76(1):390–425

    Article  MathSciNet  MATH  Google Scholar 

  • Linz P (1969) Numerial methods for Volterra integral equations with singular kernels. SIAM J Numer Anal 6(3):365–374

    Article  MathSciNet  MATH  Google Scholar 

  • Liu H, Huang J, Pan Y, Zhang J (2018) Barycentric interpolation collocation methods for solving linear and nonlinear high-dimensional Fredholm integral equations. J Comput Appl Math 327:141–154

    Article  MathSciNet  MATH  Google Scholar 

  • Lubich C (1983) Runge–Kutta theory for Volterra and Abel integral equations of the second kind. Math Comput 41(163):87–102

    Article  MathSciNet  MATH  Google Scholar 

  • Luo WH, Huang TZ, Gu XM, Liu Y (2017) Barycentric rational collocation methods for a class of nonlinear parabolic partial differential equations. Appl Math Lett 68:13–19

    Article  MathSciNet  MATH  Google Scholar 

  • Ma X, Huang C (2013) Numerical solution of fractional integro-differential equations by a hybrid collocation method. Appl Math Comput 219(12):6750–6760

    MathSciNet  MATH  Google Scholar 

  • Monegato G, Scuderi L (1998) High order methods for weakly singular integral equations with nonsmooth input functions. Math Comput 67(224):1493–1515

    Article  MathSciNet  MATH  Google Scholar 

  • Pedas A, Vainikko G (2004) Smoothing transformation and piecewise polynomial collocation for weakly singular Volterra integral equations. Computing 73(3):271–293

    Article  MathSciNet  MATH  Google Scholar 

  • te Riele HJT (1982) Collocation methods for weakly singular second-kind Volterra integral equations with non-smooth solution. IMA J Numer Anal 2(4):437–449

    Article  MathSciNet  MATH  Google Scholar 

  • Shampine LF (2008) Vectorized adaptive quadrature in matlab. J Comput Appl Math 211(2):131–140

    Article  MathSciNet  MATH  Google Scholar 

  • Zhang K, Li J, Song H (2012) Collocation methods for nonlinear convolution Volterra integral equations with multiple proportional delays. Appl Math Comput 218(22):10848–10860

    MathSciNet  MATH  Google Scholar 

  • Zhang R, Liang H, Brunner H (2016) Analysis of collocation methods for generalized auto-convolution Volterra integral equations. SIAM J Numer Anal 54(2):899–920

    Article  MathSciNet  MATH  Google Scholar 

  • Zhang R, Zhu B, Xie H (2013) Spectral methods for weakly singular Volterra integral equations with pantograph delays. Front Math China 8(2):281–299

    Article  MathSciNet  MATH  Google Scholar 

  • Zhao J, Long T, Xu Y (2019) Multistep collocation methods for Volterra integral equations with weakly singular kernels. East Asian J Appl Math 9(1):67–86

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors are grateful to the anonymous referees and the editors for their valuable comments and suggestions.

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Huazhong University of Science and Technology, Wuhan, 430074, China

    Min Li & Chengming Huang

  2. Hubei Key Laboratory of Engineering Modeling and Scientific Computing, Huazhong University of Science and Technology, Wuhan, 430074, China

    Chengming Huang

  3. School of Mathematics and Information Science, Nanchang Hangkong University, Nanchang, 330063, China

    Wanyuan Ming

Authors
  1. Min Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Chengming Huang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Wanyuan Ming
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Chengming Huang.

Additional information

Communicated by Hui Liang.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work was supported by National Natural Science Foundation of China (No. 11771163).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, M., Huang, C. & Ming, W. Barycentric rational collocation methods for Volterra integral equations with weakly singular kernels. Comp. Appl. Math. 38, 120 (2019). https://doi.org/10.1007/s40314-019-0890-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-019-0890-9

Keywords

Mathematics Subject Classification