Skip to main content
Springer Nature Link
Log in

Covering-based soft fuzzy rough theory and its application to multiple criteria decision making

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

Abstract

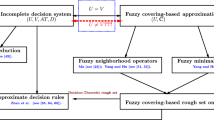
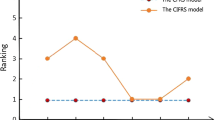
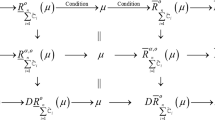
Covering-based rough set model is a vital topic as a generalization of rough sets which is a tool for AI and data mining. For the purpose, we establish two classes of hybrid uncertain systems: soft rough fuzzy-covering models and soft fuzzy rough covering models by means of (fuzzy) soft neighborhoods. By means of fuzzy soft measure degrees, we deduce \(\alpha \)-soft rough fuzzy coverings, D-soft rough fuzzy coverings, \(\alpha \)-soft fuzzy rough coverings, and D-soft fuzzy rough coverings by these two hybrid uncertain systems, respectively. The relationships among the proposed covering-based rough set models are given. Based on the theoretical discussion for the combination of covering fuzzy rough sets and soft sets, we set forth a new method to multiple criteria decision-making problem. By comparative analysis, we obtain that the optimal results are the same between the aggregation operator method and our proposed method, which means that our method is reasonable and effective.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  • Alcantud JCR (2016a) A novel algorithm for fuzzy soft set based decision making from multiobserver input parameter data set. Inf Fusion 29:142–148

    Article  Google Scholar 

  • Alcantud JCR (2016b) Some formal relationships among soft sets, fuzzy sets and their extensions. Int J Approx Reason 68:45–53

    Article  MathSciNet  MATH  Google Scholar 

  • Alcantud JCR, Santos-García G (2017) A new criterion for soft set based decision making problems under incomplete information. Int J Comput Intell Syst 10:394–404

    Article  Google Scholar 

  • Ali MI (2011) A note on soft sets, rough sets and fuzzy soft sets. Appl Soft Comput 11(4):3329–3332

    Article  Google Scholar 

  • Ali MI (2012) Another view on reduction of parameters in soft sets. Appl Soft Comput 12(6):1814–1821

    Article  Google Scholar 

  • Ali MI, Shabir M (2014) Logic connectives for soft sets and fuzzy soft sets. IEEE Trans Fuzzy Syst 22(6):1431–1442

    Article  Google Scholar 

  • Ali MI, Shabir M, Feng F (2017) Representation of graphs based on neighborhoods and soft sets. Int J Mach Learn Cybern 8:1525–1535

    Article  Google Scholar 

  • Bonikowski Z, Bryniarski E, Wybraniec-Skardowska U (1998) Extensions and intentions in rough set theory. Inf Sci 107:149–167

    Article  MathSciNet  MATH  Google Scholar 

  • Chen D, Tsang ECC, Yeung DS, Wang X (2005) The parameterization reduction of soft sets and its applications. Comput Math Appl 49:757–763

    Article  MathSciNet  MATH  Google Scholar 

  • Chen D, Wang C, Hu Q (2007) A new approach to attribute reduction of consistent and inconsistent covering decision systems with covering rough sets. Inf Sci 177:3500–3518

    Article  MathSciNet  MATH  Google Scholar 

  • D’eer L, Restrepro M, Cornelis C, Gomez J (2016) Neighborhood operators for coverings based rough sets. Inf Sci 336:21–44

    Article  MATH  Google Scholar 

  • D’eer L, Cornelis C, Godo L (2017) Fuzzy neighborhood operators based on fuzzy coverings. Fuzzy Sets Syst 312:17–35

    Article  MathSciNet  MATH  Google Scholar 

  • Deng T, Chen Y, Xu W, Dai Q (2007) A novel approach to fuzzy rough sets based on a fuzzy covering. Inf Sci 177:2308–2326

    Article  MathSciNet  MATH  Google Scholar 

  • Dubois D, Prade H (1990) Rough fuzzy sets and fuzzy rough sets. Int J Gen Syst 17:191–209

    Article  MATH  Google Scholar 

  • Feng F, Jun YB, Liu X, Li L (2010a) An adjustable approach to fuzzy soft set based decision making. J Comput Appl Math 234(1):10–20

    Article  MathSciNet  MATH  Google Scholar 

  • Feng F, Li C, Davvaz B, Ali MI (2010b) Soft sets combined with fuzzy sets and rough sets: a tentative approach. Soft Comput 14(9):899–911

    Article  MATH  Google Scholar 

  • Feng F, Liu XY, Leoreanu-Fotea V, Jun YB (2011) Soft sets and soft rough sets. Inf Sci 181(6):1125–1137

    Article  MathSciNet  MATH  Google Scholar 

  • Feng T, Zhang S, Mi J (2012) The reduction and fusion of fuzzy covering systems based on the evidence theory. Int J Approx Reaon 53:87–103

    Article  MathSciNet  MATH  Google Scholar 

  • Gong K, Wang P, Xiao Z (2013) Bijective soft set decision system based parameters reduction under fuzzy environments. Appl Math Model 37:4474–4485

    Article  MathSciNet  MATH  Google Scholar 

  • Han B, Li Y, Liu J, Geng S, Li H (2014) Elicitation criterions for restricted intersection of two incomplete soft sets. Knowl Based Syst 59:121–131

    Article  Google Scholar 

  • Han B, Li Y, Geng S (2017) 0–1 Linear programming methods for optimal normal and pseudo parameter reduction of soft sets. Appl Soft Comput 54:467–484

    Article  Google Scholar 

  • Herawan T, Deris MM (2011) A soft set approach for association rules mining. Knowl Based Syst 24(1):186–195

    Article  Google Scholar 

  • Kong Z, Jia W, Zhang G, Wang L (2015) Normal parameter reduction in soft set based on particle swarm optimization algorithm. Appl Math Model 39:4808–4820

    Article  MathSciNet  Google Scholar 

  • Li Z, Xie T (2014) The relationships among soft sets, soft rough sets and topologies. Soft Comput 18:717–728

    Article  MATH  Google Scholar 

  • Li TJ, Leung Y, Zhang WX (2008) Generalized fuzzy rough approximation operators based on fuzzy covering. Int J Approx Reason 48:836–856

    Article  MathSciNet  MATH  Google Scholar 

  • Li Z, Xie N, Wen G (2015) Soft coverings and their parameter reductions. Appl Soft Comput 31:48–60

    Article  Google Scholar 

  • Liu GL, Sai Y (2009) A comparison of two types of rough sets induced by coverings. Int J Approx Reason 50:521–528

    Article  MathSciNet  MATH  Google Scholar 

  • Ma L (2012) On some types of neighborhood-related covering rough sets. Int J Approx Reason 53:901–911

    Article  MathSciNet  MATH  Google Scholar 

  • Ma L (2015) Some twin approximation operators on covering approximation spaces. Int J Approx Reason 56:59–70

    Article  MathSciNet  MATH  Google Scholar 

  • Ma L (2016) Two fuzzy coverings rough set models and their generalizations over fuzzy lattices. Fuzzy Sets Syst 294:1–17

    Article  MathSciNet  MATH  Google Scholar 

  • Ma X, Liu Q, Zhan J (2017) A survey of decision making methods based on certain hybrid soft set models. Artif Intell Rev 47:507–530

    Article  Google Scholar 

  • Ma X, Zhan J, Ali MI, Mehmood N (2018) A survey of decision making methods based on two classes of hybrid soft set models. Artif Intell Rev 49(4):511–529

    Article  Google Scholar 

  • Mahmood T, Ali MI, Hussain A (2018) Generalized roughness in fuzzy filters and fuzzy ideals with thresholds in ordered semigroups. Comput Appl Math 37:5013–5033

    Article  MathSciNet  MATH  Google Scholar 

  • Maji PK, Roy AR, Biswas R (2002) An application of soft sets in a decision making problem. Comput Math Appl 44(8):1077–1083

    Article  MathSciNet  MATH  Google Scholar 

  • Maji PK, Biswas R, Roy AR (2003) Soft set theory. Comput Math Appl 45(4):555–562

    Article  MathSciNet  MATH  Google Scholar 

  • Mardani A, Jusoh A, Zavadskas EK (2015) Fuzzy multiple criteria decision-making techniques and applications—two decades review from 1994 to 2014. Expert Syst Appl 42(8):4126–4148

    Article  Google Scholar 

  • Meng D, Zhang X, Qin K (2011) Soft rough fuzzy sets and soft fuzzy rough sets. Comput Math Appl 62(12):4635–4645

    Article  MathSciNet  MATH  Google Scholar 

  • Molodtsov D (1999) Soft set theory-first results. Comput Math Appl 37(4):19–31

    Article  MathSciNet  MATH  Google Scholar 

  • Pawlak Z (1982) Rough sets. Int J Comput Inf Sci 11(5):341–356

    Article  MATH  Google Scholar 

  • Pawlak Z (1998) Rough sets in Knowledge. Physica, Heidelberg

    Google Scholar 

  • Peng X, Li W (2019) Algorithms for interval-valued fuzzy soft sets in emergency decision making based on WDBA and CODAS with new information measure. IEEE Access 7:7419–7441

    Article  Google Scholar 

  • Peng X, Liu C (2017) Algorithms for neutrosophic soft decision making based on EDAS, new similarity measure and level soft set. J Intell Fuzzy Syst 32:955–968

    Article  MATH  Google Scholar 

  • Peng X, Yang Y (2017) Algorithms for interval-valued fuzzy soft sets in stochastic multi-criteria decision making based on regret theory and prospect theory with combined weight. Appl Soft Comput 54:415–430

    Article  Google Scholar 

  • Pomykala JA (1987) Approximation operations in approximation spaces. Bull Pol Acad Sci Math 35:653–662

    MathSciNet  MATH  Google Scholar 

  • Qin K, Pei Z (2005) On the topological properties of fuzzy rough sets. Fuzzy Sets Syst 151:601–613

    Article  MathSciNet  MATH  Google Scholar 

  • Rehman N, Ali A, Ali MI, Park C (2018) SDMGRS: soft dominance based multi granulation rough sets and their applications in conflict analysis problems. IEEE Access 6:31399–31416

    Article  Google Scholar 

  • Shabir M, Ali MI, Shaheen T (2013) Another approach to soft rough sets. Knowl Based Syst 40(1):72–80

    Article  Google Scholar 

  • Shah N, Mehmood N, Rehman N, Shabir M, Ali MI (2018a) Z-soft rough fuzzy graphs: a new approach to decision making. J Intell Fuzzy Syst 35(4):4879–4891

    Article  Google Scholar 

  • Shah N, Rehman N, Shabir M, Ali MI (2018b) Another approach to roughness of soft graphs with applications in decision making. Symmetry 10(5):145

    Article  Google Scholar 

  • Sun B, Ma W (2014) Soft fuzzy rough sets and its application in decision making. Artif Intell Rev 41(1):67–80

    Article  Google Scholar 

  • Sun B, Ma W, Qian Y (2017a) Multigranulation fuzzy rough set over two universes and its application to decision making. Knowl Based Syst 123:61–74

    Article  Google Scholar 

  • Sun B, Ma W, Li X (2017b) Linguistic value soft set-based approach to multiple criteria group decision-making. Appl Soft Comput 58:285–296

    Article  Google Scholar 

  • Sun B, Ma W, Xiao X (2017c) Three-way group decision making based on multigranulation fuzzy decision-theoretic rough set over two universes. Int J Approx Reason 81:87–102

    Article  MathSciNet  MATH  Google Scholar 

  • Tsang ECC, Chen D, Yeung DS (2008) Approximations and reducts with covering generalized rough sets. Comput Appl Math 56:279–289

    Article  MathSciNet  MATH  Google Scholar 

  • Wang C, Chen D, Wu C, Hu Q (2011) Data compression with homomorphsim in covering information systems. Int J Approx Reason 52:519–525

    Article  MATH  Google Scholar 

  • Wu WZ, Zhang WX (2004) Neighborhood operator systems and approximation operators. Inf Sci 159:233–254

    Article  Google Scholar 

  • Xiao Z, Gong K, Zou Y (2009) A combined forecasting approach based on fuzzy soft sets. J Comput Appl Math 228:326–333

    Article  MathSciNet  MATH  Google Scholar 

  • Xiao Z, Chen W, Li L (2013) A method based on interval-valued fuzzy soft set for multi-attribute group decision-making problems under uncertain environment. Knowl Inf Syst 34:653–669

    Article  Google Scholar 

  • Xu WH, Zhang WX (2007) Measuring roughness of generalized rough sets induced a covering. Fuzzy Sets Syst 158:2443–2455

    Article  MathSciNet  MATH  Google Scholar 

  • Yager RR (1998) On ordered weighted averaging aggregation operators in multicriteria decisionmaking. IEEE Trans Syst Man Cybern 18:183–190

    Article  MathSciNet  MATH  Google Scholar 

  • Yang B, Hu BQ (2016) A fuzzy covering-based rough set model and its generalization over fuzzy lattice. Inf Sci 367–368:463–486

    Article  Google Scholar 

  • Yang B, Hu BQ (2017) On some types of fuzzy covering-based on rough sets. Fuzzy Sets Syst 312:36–65

    Article  MathSciNet  MATH  Google Scholar 

  • Yao YY (1998) Relational interpretations of neighborhood operators and rough set approximation operators. Inf Sci 111:239–259

    Article  MathSciNet  MATH  Google Scholar 

  • Yao YY, Deng X (2014) Quantitative rough sets based on subsethood measures. Inf Sci 267:306–322

    Article  MathSciNet  MATH  Google Scholar 

  • Yao YY, Yao B (2012) Covering based rough set approximations. Inf Sci 200:91–107

    Article  MathSciNet  MATH  Google Scholar 

  • Yeung DS, Chen D, Lee J, Wang X (2015) On the generalization of fuzzy rough sets. IEEE Trans Fuzzy Syst 13:343–361

    Article  Google Scholar 

  • Yuksel S, Ergul ZG, Tozlu N (2014) Soft covering based rough sets and their applications. Sci World J, Article 970893

  • Yuksel S, Tozlu N, Dizman TH (2015) An application of multicriteria group decision making by soft covering based rough sets. Filomat 29:209–219

    Article  MathSciNet  MATH  Google Scholar 

  • Zadeh LA (1965) Fuzzy sets. Inf Control 8:338–353

    Article  MATH  Google Scholar 

  • Zhan J, Alcantud JCR (2018) A novel type of soft rough covering and its application to multicriteria group decision making. Artif Intell Rev. https://doi.org/10.1007/s10462-018-9617-3

  • Zhan J, Wang Q (2019) Certain types of soft coverings based rough sets with applications. Int J Mach Learn Cybern 10:1065–1076

    Article  Google Scholar 

  • Zhan J, Zhu K (2015) Reviews on decision making methods based on (fuzzy) soft sets and rough soft sets. J Intell Fuzzy Syst 29:1169–1176

    Article  MathSciNet  MATH  Google Scholar 

  • Zhan J, Zhu K (2017) A novel soft rough fuzzy set: \(Z\)-soft rough fuzzy ideals of hemirings and corresponding decision making. Soft Comput 21:1923–1936

    Article  MATH  Google Scholar 

  • Zhan J, Liu Q, Davvaz B (2015) A new rough set theory: rough soft hemirings. J Intell Fuzzy Syst 28:1687–1697

    MathSciNet  MATH  Google Scholar 

  • Zhan J, Ali MI, Mehmood N (2017a) On a novel uncertain soft set model: \(Z\)-soft fuzzy rough set model and corresponding decision making methods. Appl Soft Comput 56:446–457

    Article  Google Scholar 

  • Zhan J, Liu Q, Herawan T (2017b) A novel soft rough set: soft rough hemirings and corresponding multicriteria group decision making. Appl Soft Comput 54:393–402

    Article  Google Scholar 

  • Zhang L, Zhan J (2019) Fuzzy soft \(\beta \)-covering based fuzzy rough sets and corresponding decision-making applications. Int J Mach Learn Cybern 10:1487–1502

    Article  Google Scholar 

  • Zhang Z, Wang C, Tian D (2014) A novel approach to interval-valued intuitionistic fuzzy soft sets based decision making. Appl Math Model 38(4):1255–1270

    Article  MathSciNet  MATH  Google Scholar 

  • Zhang XH, Miao D, Liu C, Le M (2016) Constructive methods of rough approximation operators and multigranuation rough sets. Knowl Based Syst 91:114–125

    Article  Google Scholar 

  • Zhu W (2007) Topological approaches to covering rough sets. Inf Sci 177:1499–1508

    Article  MathSciNet  MATH  Google Scholar 

  • Zhu W (2009a) Relationship between generalized rough sets based on binary relation and covering. Inf Sci 179(3):210–225

    Article  MathSciNet  MATH  Google Scholar 

  • Zhu W (2009b) Relationships among basic concepts in covering-based rough sets. Inf Sci 179:2478–2486

    Article  MathSciNet  MATH  Google Scholar 

  • Zhu W, Wang F (2003) Reduction and axiomization of covering generalized rough sets. Inf Sci 152:217–230

    Article  MathSciNet  MATH  Google Scholar 

  • Zou Y, Xiao Z (2008) Data analysis approaches of soft sets under incomplete information. Knowl Based Syst 21(8):941–945

    Article  Google Scholar 

Download references

Acknowledgements

The authors are thankful to associate editor and anonymous referees for their valuable comments on our manuscript. This research was supported by NNSFC (61866011; 11561023; 71571090; 61772019), the Fundamental Research Funds for the Central Universities (JB190602), the Youth Innovation Team of Shaanxi Universities, the Interdisciplinary Foundation of Humanities and Information (RW180167), and the National Science Foundation of Hubei Province (2017CFB353).

Author information

Authors and Affiliations

  1. Department of Mathematics, Hubei Minzu University, Enshi, 445000, China

    Jianming Zhan

  2. School of Economics and Management, Xidian University, Xi’an, 710071, China

    Bingzhen Sun

Authors
  1. Jianming Zhan
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Bingzhen Sun
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Jianming Zhan.

Ethics declarations

Conflict of interest

All authors declare that there is no conflict of interest regarding this manuscript.

Additional information

Communicated by Marcos Eduardo Valle.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhan, J., Sun, B. Covering-based soft fuzzy rough theory and its application to multiple criteria decision making. Comp. Appl. Math. 38, 149 (2019). https://doi.org/10.1007/s40314-019-0931-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-019-0931-4

Keywords

Mathematics Subject Classification