Abstract
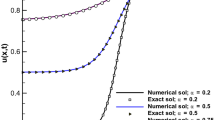
A fourth-order diffusion model is presented with a nonlinear reaction term to simulate some special chemical and biological phenomenon. To obtain the solutions to those problems, the nonlinear Galerkin finite element method under the framework of the Hermite polynomial function for the spatial domain is utilized. The Euler backward difference method is used to solve the equation in the temporal domain. Subject to the Dirichlet and Navier boundary conditions, the numerical experiments for Bi-flux Fisher–Kolmogorov model present excellent convergence, accuracy and acceleration behavior. Also, the numerical solutions to the Bi-flux Gray–Scott model, subject to no flux boundary conditions, show excellent convergence, accuracy and symmetry.






Similar content being viewed by others
References
Akrivis G (1996) High-order finite element methods for the Kuramoto–Sivashinsky equation. ESAIM M M Num Anal 30(2):157–183
Araujo ALA (2014) Periodic solutions for extended Fisher–Kolmogorov and Swift–Hohenberg equations obtained using a continuation theorem. Nonlinear Anal 94:100–106
Bevilacqua L, Galeão ACNR, Costa FP (2011) On the significance of higher order terms in diffusion processes. J Braz Soc Mech Sci Eng 34(2):166–175
Bevilacqua L, Galeão ACNR, Simas JG, Doce APR (2013) A new theory for anomalous diffusion with a bimodal flux distribution. J Braz Soc Mech Sci Eng 35(4):431–440
Bevilacqua L, Jiang M, Silva Neto AJ, Galeão ACNR (2016) An evolutionary model of bi-flux diffusion processes. J Braz Soc Mech Sci Eng 38(5):1421–1432
Chunk SK, Pani AK (2001) Numerical methods for the Rosenau equation. Appl Anal 77(3–4):351–369
Danumjaya P, Pani KA (2005) Orthogonal cubic spline collocation method for the extended Fisher–Kolmogorov equation. J Comput Appl Math 174(1):101–117
Dee GT, Saarloos W (1988) Bistable systems with propagating fronts leading to pattern formation. Phys Rev Lett 60:2641
Dettopri L, Gottlieb D, Temam R (1995) A nonlinear Galerkin method: the two-level Fourier-collocation case. J Sci Comput 10(4):371–389
Doelman A, Kaper TJ, Zegeling P (1997) Pattern formation in 1D Gray–Scott model. Nonlinearity 10:523–563
Dubois T, Jauberteau F, Temam R (1998) Incremental unknowns, multilevel methods and the numerical simulation of turbulence. Com Met A Mech Eng 159(1–2):123–189
Dubois T, Jauberteau F, Temam R (1999) Dynamic multilevel methods and the numerical simulation of turbulence. Cambridge University Press, Cambridge
Dubois T, Jauberteau F, Temam R (2004) Multilevel methods in turbulence. Encyclopedia of computational mechanics. Wiley, New York
Elliott CM, French DA (1987) Numerical studies of the Cahn-Hilliard equation for the phase seperation. IMA J Appl Math 38(2):97–128
Elliott CM, Zheng S (1986) On the Cahn–Hilliard equation Arch. Rat Mech Anal 96:399
Hobbs RE (1981) Pipeline buckling caused by axial loads. J Constr Steel Res 1(2):2–10
Jiang M (2017) The fourth order diffusion model for bi-flux mass transfer. PhD. dissertation, Federal University of Rio de Janeiro
Jiang M, Bevilacqua L, Silva Neto AJ, Galeão ACNR, Zhu J (2018) Bi-flux theory applied to the dispersion of particles in anisotropic substratum. Appl Math Model 64:121–134
Khiari N, Omrani K (2011) Finite difference discretization of the extended Fisher–Kolmogorov equation in two dimensions. Comput Math Appl 62(11):4151–4160
Laminie J, Pascal F, Temam R (1993) Implementation of finite element nonlinear Galerkin methods using hierarchical bases. Comput Mech 11(5–6):384–407
Lee KJ, McCormick WD, Pearson JE, Swinney HL (1994) Experimental observation of self-replicating spots in a reaction–diffusion system. Nature 369:215–218
Liu R, Wang W, Yan S (2013) Pipeline buckling caused by axial loads. J Cent South Univ 20(1):236–245
Marion M, Temam R (1989) Nonlinear Galerkin methods SIAM. J Numer Anal 26(5):1139–1157
Marion M, Temam R (1990) Nonlinear Galerkin methods: the finite elements case Numer. Mathematics 57(1):205–226
Marion M, Xu J (1995) Error estimates on a new nonlinear Galerkin method based on two-grid finite elements SIAM. J Numer Anal 32(4):1170–1184
Pearson JE (1993) Complex patterns in a simple system. Science 261:189–192
Peletier LA (1996) Chaotic spatial patterns described by the extended Fisher–Kolmogorov equation. J Differ Equ 129(2):458–508
Peletier LA, Troy WC (1996) Spatial patterns described by the extended Fisher–Kolmogorov equation: periodic solutions. J Math Anal 28(6):1317–1353
Qiang DU, Nicolaides RA (1991) Numerical analysis of continuum model of phase transition. SIAM J Numer Anal 28(5):1310–1322
Turing AM (1952) The chemical basis of morphogenesis. Philos Trans R Soc Lond B 237:37–72
Zhang R, Zhu J, Loula AFD, Yu X (2016) A new nonlinear Galerkin finite element method for the computation of reaction diffusion equations. J Math Anal Appl 434(1):136–148
Zhang J, Zhu J, Zhang R, Yang D, Loula AFD (2017) A combined discontinuous Galerkin finite element method for miscible displacement problem. J Comput Appl Math 309(1):44–55
Acknowledgements
Jiang Zhu’s work was partially supported by the National Council for Scientific and Technological Development of Brazil (CNPq). Xijun Yu’s work was supported partially by the National Natural Science Foundation of China (Grant No. 11571002, 11772067, 11702028) and CAEP Foundation of China (Grant No. CX2019032). Luiz Bevilacqua’s work was supported partially by CNPq/TWAS Grant, the COPPE/CAPES Grant 001, and the USP/IEA visiting research program. Maosheng Jiang’s work was supported partially by CNPq/TWAS Grant.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Abimael Loula.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Jiang, M., Bevilacqua, L., Zhu, J. et al. Nonlinear Galerkin finite element methods for fourth-order Bi-flux diffusion model with nonlinear reaction term. Comp. Appl. Math. 39, 143 (2020). https://doi.org/10.1007/s40314-020-01168-w
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40314-020-01168-w