Skip to main content
Springer Nature Link
Log in

Quasi-invariant and attractive sets of inertial neural networks with time-varying and infinite distributed delays

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

Abstract

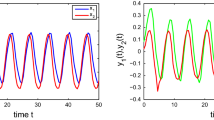
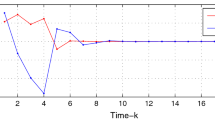
This paper aims at analyzing the quasi-invariant and attractive sets for a class of inertial neural networks with time-varying and infinite distributed delays. By utilizing the properties of nonnegative matrix, a new bidirectional-like delay integral inequality is developed. Some sufficient conditions are obtained for the existence of the quasi-invariant and attractive sets of the discussed system according to the bidirectional-like integral inequality. Besides, the framework of the quasi-invariant and attractive sets for the concerned system is provided. Finally, one example is analyzed to clarify the validity of our results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  • Berman A, Plemmons RJ (1979) Nonnegative matrices in mathematical sciences. Academic Press, New York

    MATH  Google Scholar 

  • Cao JD, Wan Y (2014) Matrix measure strategies for stability and synchronization of inertial BAM neural network with time delays. Neural Netw. 53:165–172

    Article  Google Scholar 

  • Cui N, Jiang HJ, Hu C, Abdurahman A (2018) Global asymptotic and robust stability of inertial neural networks with proportional delays. Neurocomputing 272:326–333

    Article  Google Scholar 

  • He X, Li CD, Shu YL (2012) Bogdanov-Takens bifurcation in a single inertial neuron model with delay. Neurocomputing 89:193–201

    Article  Google Scholar 

  • Horn RA, Johnson CR (1985) Matrix analysis. Cambridge University Press, Cambridge

    Book  Google Scholar 

  • Jian JG, Wan P (2015) Global exponential convergence of generalized chaotic systems with multiple time-varying and finite distributed delays. Physica A 431:152–165

    Article  MathSciNet  Google Scholar 

  • Ke YQ, Miao CF (2017) Anti-periodic solutions of inertial neural networks with time delays. Neural Process. Lett. 45:523–538

    Article  Google Scholar 

  • Li HF, Li CD, Huang TW (2017) Periodicity and stability for variable-time impulsive neural networks. Neural Netw. 94:24–33

    Article  Google Scholar 

  • Li XY, Li XT, Hu C (2017) Some new results on stability and synchronization for delayed inertial neural networks based on non-reduced order method. Neural Netw. 96:91–100

    Article  Google Scholar 

  • Li YP, Liao XF, Li HQ (2016) Global attracting sets of non-autonomous and complex-valued neural networks with time-varying delays. Neurocomputing 173:994–1000

    Article  Google Scholar 

  • Li DS, Xu DY (2013) Attracting and quasi-invariant sets of stochastic neutral partial functional differential equations. Acta Math. Sci. 33:578–588

    Article  MathSciNet  Google Scholar 

  • Liao XX, Luo Q, Zeng ZG (2008) Positive invariant and global exponential attractive sets of neural networks with time-varying delays. Neurocomputing 71:513–518

    Article  Google Scholar 

  • Manivannan R, Samidurai R, Cao JD, Alsaedi A, Alsaadi FE (2018) Design of extended dissipativity state estimation for generalized neural networks with mixed time-varying delay signals. Inform. Sci. 424:175–203

    Article  MathSciNet  Google Scholar 

  • Qi JT, Li CD, Huang TW (2015) Stability of inertial BAM neural network with time-varying delay via impulsive control. Neurocomputing 161:162–167

    Article  Google Scholar 

  • Song QK, Shu HQ, Zhao ZJ, Liu YR, Alsaadi FE (2017) Lagrange stability analysis for complex-valued neural networks with leakage delay and mixed time-varying delays. Neurocomputing 244:33–41

    Article  Google Scholar 

  • Tang Q, Jian JG (2019) Exponential synchronization of inertial neural networks with mixed time-varying delays via periodically intermittent control. Neurocomputing 338:181–190

    Article  Google Scholar 

  • Tang Q, Jian JG (2019) Global exponential convergence for impulsive inertial complex-valued neural networks with time-varying delays. Math. Comput. Simul. 159:39–56

    Article  MathSciNet  Google Scholar 

  • Tang Q, Jian JG (2018) Matrix measure based exponential stabilization for complex-valued inertial neural networks with time-varying delays using impulsive control. Neurocomputing 273:251–259

    Article  Google Scholar 

  • Tu ZW, Cao JD, Alsaedi A, Alsaadi F (2017) Global dissipativity of memristor-based neutral type inertial neural networks. Neural Netw. 88:125–133

    Article  Google Scholar 

  • Tu ZW, Cao JD, Hayat T (2016) Global exponential stability in Lagrange sense for inertial neural networks with time-varying delays. Neurocomputing 171:524–531

    Article  Google Scholar 

  • Tu ZW, Jian JG, Wang BX (2011) Positive invariant sets and global exponential attractive sets of a class of neural networks with unbounded time-delays. Commun. Nonlinear Sci. Numer. Simul. 16:3738–3745

    Article  MathSciNet  Google Scholar 

  • Velmurugan G, Rakkiyappan R, Cao JD (2016) Finite-time synchronization of fractional-order memristor-based neural networks with time delays. Neural Netw. 73:36–46

    Article  Google Scholar 

  • Velmurugan G, Rakkiyappan R, Vembarasan V, Cao JD, Alsaedi A (2017) Dissipativity and stability analysis of fractional-order complex-valued neural networks with time delay. Neural Netw. 86:42–53

    Article  Google Scholar 

  • Wan P, Jian JG (2017) Global convergence analysis of impulsive inertial neural networks with time-varying delays. Neurocomputing 245:68–76

    Article  Google Scholar 

  • Wang JF, Tian LX (2017) Global Lagrange stability for inertial neural networks with mixed time-varying delays. Neurocomputing 235:140–146

    Article  Google Scholar 

  • Wheeler DW, Schieve WC (1997) Stability and chaos in an inertial two-neuron system. Physica D 105:267–284

    Article  Google Scholar 

  • Xu CJ, Li PL (2017) Global exponential stability of periodic solution for fuzzy cellular neural networks with distributed delays and variable coefficients. J. Int. Fuzzy Syst. 32:2603–2615

    MATH  Google Scholar 

  • Xu DY, Long SJ (2012) Attracting and quasi-invariant sets of non-autonomous neural networks with delays. Neurocomputing 77:222–228

    Article  Google Scholar 

  • Zhang W, Huang TW, He X, Li CD (2017) Global exponential stability of inertial memristor-based neural networks with time-varying delays and impulses. Neural Netw. 95:102–109

    Article  Google Scholar 

  • Zhang ZQ, Quan ZY (2015) Global exponential stability via inequality technique for inertial BAM neural networks with time delays. Neurocomputing 151:1316–1326

    Article  Google Scholar 

  • Zhang ZQ, Yu SH (2016) Global asymptotic stability for a class of complex-valued Cohen-Grossberg neural networks with time delays. Neurocomputing 171:1158–1166

    Article  Google Scholar 

  • Zhang FH, Zeng ZG (2018) Multistability and instability analysis of recurrent neural networks with time-varying delays. Neural Netw. 97:116–126

    Article  Google Scholar 

  • Zhang GD, Zeng ZG (2018) Exponential stability for a class of memristive neural networks with mixed time-varying delays. Appl. Math. Comput. 321:544–554

    MathSciNet  MATH  Google Scholar 

  • Zhang GD, Zeng ZG, Hu JH (2018) New results on global exponential dissipativity analysis of memristive inertial neural networks with distributed time-varying delays. Neural Netw. 97:183–191

    Article  Google Scholar 

  • Zhao ZH, Jian JG (2014) Attracting and quasi-invariant sets for BAM neural networks of neutral-type with time-varying and infinite distributed delays. Neurocomputing 140:265–272

    Article  Google Scholar 

  • Zhao ZH, Jian JG (2014) Positive invariant sets and global exponential attractive sets of BAM neural networks with time-varying and infinite distributed delays. Neurocomputing 142:447–457

    Article  Google Scholar 

Download references

Acknowledgements

The authors are grateful for the support of the National Natural Science Foundation of China (U1731124).

Author information

Authors and Affiliations

  1. College of Science, China Three Gorges University, Yichang, 443002, Hubei, China

    Qian Tang & Jigui Jian

  2. Three Gorges Mathematical Research Center, China Three Gorges University, Hubei, Yichang, 443002, China

    Qian Tang & Jigui Jian

Authors
  1. Qian Tang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jigui Jian
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Jigui Jian.

Additional information

Communicated by Leonardo Tomazeli Duarte.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tang, Q., Jian, J. Quasi-invariant and attractive sets of inertial neural networks with time-varying and infinite distributed delays. Comp. Appl. Math. 39, 158 (2020). https://doi.org/10.1007/s40314-020-01186-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-020-01186-8

Keywords

Mathematics Subject Classification