Skip to main content
Springer Nature Link
Log in

Certain methods to solve bipolar fuzzy linear system of equations

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

Abstract

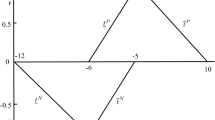
In this article, we present two different analytical methods based on embedding technique and bipolar fuzzy center to solve bipolar fuzzy linear system (BFLS) of equations. In the first method, to solve BFLS of equations, we replace BFLS of equations by a pair of positive\((*)\) and negative\((\bullet )\) two \(n \times n\) crisp linear systems. We provide the necessary and sufficient conditions for the solution of BFLS of equations. In the second method, we use the graphical technique and apply bipolar fuzzy center to draw a graph at some specific end points to solve the BFLS of equations. Further, we develop a technique to solve the fully bipolar fuzzy linear system of equations. We present solutions of some numerical examples to show the effectiveness of the proposed techniques.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  • Abbasbandy S, Alavi M (2005) A method for solving fuzzy linear systems. Fuzzy Sets Syst 2(2):37–43

    MathSciNet  MATH  Google Scholar 

  • Abbasbandy S, Jafarian A (2006) Steepest descent method for system of fuzzy linear equations. Appl Math Comput 175(1):823–833

    MathSciNet  MATH  Google Scholar 

  • Akram M, Arshad M (2019) A novel trapezoidal bipolar fuzzy TOPSIS method for group decision-making. Group Decis Negot 28(3):565–584

    Google Scholar 

  • Akram M, Muhammad G, Koam AN, Hussain N (2019a) Iterative methods for solving a system of linear equations in a bipolar fuzzy environment. Mathematics 7(8):728

    Google Scholar 

  • Akram M, Muhammad G, Allahviranloo T (2019b) Iterative methods for solving a system of linear equations in a bipolar fuzzy environment. Mathematics 7(8):728

    Google Scholar 

  • Akram M, Muhammad G, Hussian N (2019c) Bipolar fuzzy system of linear equations with polynomial parametric form. J Intell Fuzzy Syst 37(6):8275–8287

    Google Scholar 

  • Akram M, Saleem D, Allahviranloo T (2019d) Linear system of equations in m-polar fuzzy environment. J Intell Fuzzy Syst 37(6):8251–8266

    Google Scholar 

  • Akram M, Muhammad G, Allahviranloo T (2019e) Bipolar fuzzy linear system of equations. Comput Appl Math 38(2):69

    MathSciNet  MATH  Google Scholar 

  • Allahviranloo T (2004) Numerical methods for fuzzy system of linear equations. Appl Math Comput 155(2):493–502

    MathSciNet  MATH  Google Scholar 

  • Allahviranloo T (2005a) Successive over relaxation iterative method for fuzzy system of linear equations. Appl Math Comput 162(1):189–196

    MathSciNet  MATH  Google Scholar 

  • Allahviranloo T (2005b) The Adomian decomposition method for fuzzy system of linear equations. Appl Math Comput 163(2):553–563

    MathSciNet  MATH  Google Scholar 

  • Allahviranloo T (2019) Uncertain information and linear systems, studies in systems, decision and control. Springer, Berlin, p 254

    Google Scholar 

  • Dubois D, Prade H (1978) Operations on fuzzy numbers. Int J Syst Sci 9:613–626

    MathSciNet  MATH  Google Scholar 

  • Friedman M, Ming MMa, Kandel A (1998) Fuzzy linear systems. Fuzzy Sets Syst 96:201–209

    MathSciNet  MATH  Google Scholar 

  • Minc H (1988) Nonnegative matrices. Wiley, New York

    MATH  Google Scholar 

  • Ming M, Friedman M, Kandel A (1999) A new fuzzy arithmetic. Fuzzy Sets Syst 108(1):83–90

    MathSciNet  MATH  Google Scholar 

  • Senthilkumar P, Rajendran G (2009) Solution of fuzzy linear systems by using fuzzy centre. Appl Math Sci 3(49):2411–2419

    MathSciNet  MATH  Google Scholar 

  • Suparna D, Chakraverty S (2011) Numerical solution of interval and fuzzy system of linear equations. Doctoral dissertation

  • Zadeh LA (1965) Fuzzy sets. Inf Control 8(3):338–353

    MATH  Google Scholar 

  • Zadeh LA (1975) The concept of a linguistic and application to approximate reasoning-I. Inf Sci 8:199–249

    MathSciNet  MATH  Google Scholar 

  • Zhang WR (1994) Bipolar fuzzy sets and relations: a computational framework forcognitive modeling and multiagent decision analysis. In: Proceedings of IEEE conference, pp 305–309

  • Zhang WR (1998) YinYang Bipolar fuzzy sets. In: IEEE world congress on fuzzy systems proceedings. Computational Intelligence, pp 835–840

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, University of the Punjab, New Campus, Lahore, Pakistan

    Muhammad Akram & Muhammad Ali

  2. Faculty of Engineering and Natural Sciences, Bahcesehir University, Istanbul, Turkey

    Tofigh Allahviranloo

Authors
  1. Muhammad Akram
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Muhammad Ali
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Tofigh Allahviranloo
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Tofigh Allahviranloo.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest regarding the publication of the research article.

Additional information

Communicated by Leonardo Tomazeli Duarte.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Akram, M., Ali, M. & Allahviranloo, T. Certain methods to solve bipolar fuzzy linear system of equations. Comp. Appl. Math. 39, 213 (2020). https://doi.org/10.1007/s40314-020-01256-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-020-01256-x

Keywords

Mathematics Subject Classification