On the transient response of plates on fractionally damped viscoelastic foundation

Abstract

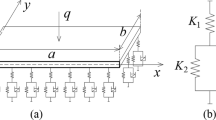
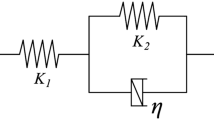
This work underlines the importance of the application of fractional-order derivative damping model in the modelling of the viscoelastic foundation, by demonstrating the effect of various orders of the fractional derivative on the dynamic response of plates resting on the viscoelastic foundation, subjected to concentrated step load. The foundation of the plate is modelled as a fractionally-damped Kelvin–Voigt model. Modal superposition method and Triangular strip matrix approach are used to solve the partial fractional differential equations of motion. The influence of (a) fractional-order derivative, (b) foundation stiffness, and (c) foundation damping viscosity parameter on the dynamic response of the plate are investigated. Theoretical results show that with the increase in the order of derivative, the damping of the system increases, which leads to decreased dynamic response. The results obtained from the fractional-order damping model and integer-order damping model are compared. The results are verified with literature and numerical results (ANSYS).

Appendix A

1.1 Triangular strip matrix approach for the integer/fractional order differential equations

The triangular strip matrix approach is a powerful numerical technique, which can be used for the solution of the integer- and fractional-order differential equations (Podlubny 2000). This approach deals with matrices of a specific structure, which are called triangular strip matrices. The properties and operations of the triangular strip matrices are discussed in details (Podlubny 2000; Podlubny et al. 2009). The approach represents the matrix form (lower triangular strip matrix or upper triangular strip matrix) of integer/fractional-order differential equations. The differential equation may contain integer-order derivative and/or the fractional-order derivative terms as seen in Eq. (19). According to the triangular matrix approach, each term of the differential equation has to be represented in the matrix form. In this work, each term is represented in the form of a lower triangular strip matrix. The following steps are used to solve the fractional differential equation Eq. 19, to find the modal generalized coordinate $\zeta \left(t\right)$. Consider a function $\zeta \left(t\right)$, defined in [a, b], the matrix form representation of its integer/fractional order derivatives can be performed by the following steps.

Step 1: Create equidistant nodes with constant step size h: ${t}_{p}=a+ph\left(p=\mathrm{0,1},2,. . .,N\right)$, in the range$\left[a,b\right]$, where ${t}_{0}=a$ and${t}_{N}=a+Nh= b$.

Step 2: Matrix representation of integer-order derivative. Let us consider the approximation of the first-order derivative ${\zeta }^{^{\prime}}\left(t\right)$ at the various interval points${t}_{p}$,$p=\mathrm{0,1},2,. . .,N$, using first-order backward differences:

$${\zeta }^{^{\prime}}\left({t}_{p}\right)\approx \frac{1}{h}\nabla \zeta \left({t}_{p}\right)=\frac{1}{h}\left({\zeta }_{p}-{\zeta }_{p-1}\right), \quad p=\mathrm{1,2},\dots ,N.$$

(A.1)

The above expression can be written in matrix form as:

$$\left[\begin{array}{c}{h}^{-1}{\zeta }_{0}\\ {h}^{-1}\nabla \zeta \left({t}_{1}\right)\\ {h}^{-1}\nabla \zeta \left({t}_{2}\right)\\ \vdots \\ {h}^{-1}\nabla \zeta \left({t}_{N-1}\right)\\ {h}^{-1}\nabla \zeta \left({t}_{N}\right)\end{array}\right]=\frac{1}{h}\left[\begin{array}{cccccc}1& 0& 0& 0& \cdots & 0\\ -1& 1& 0& 0& \cdots & 0\\ 0& -1& 1& 0& \cdots & 0\\ \cdots & \cdots & \cdots & \ddots & \cdots & \cdots \\ 0& \cdots & 0& -1& 1& 0\\ 0& 0& \cdots & 0& -1& 1\end{array}\right]\left[\begin{array}{c}{\zeta }_{0}\\ {\zeta }_{1}\\ {\zeta }_{2}\\ \vdots \\ {\zeta }_{N-1}\\ {\zeta }_{N}\end{array}\right]$$

(A.2)

Similarly, the approximation of the second-order derivative ${\zeta }^{{{\prime\prime}}}\left(t\right)$ using second-order backward differences:

$${\zeta }^{{{\prime\prime}}}\left({t}_{p}\right)\approx \frac{1}{{h}^{2}}{\nabla }^{2}\zeta \left({t}_{p}\right)=\frac{1}{{h}^{2}}\left({\zeta }_{p}-{2\zeta }_{p-1}+{\zeta }_{p-2}\right), \quad p=\mathrm{2,3},\dots ,N.$$

(A.3)

The matrix form of the second-order derivative can be represented as:

$$\left[\begin{array}{c}{h}^{-2}{\zeta }_{0}\\ {h}^{-2}\left(-2{\zeta }_{0}+{\zeta }_{1}\right)\\ {h}^{-2}\nabla \zeta \left({t}_{2}\right)\\ \vdots \\ {h}^{-2}\nabla \zeta \left({t}_{N-1}\right)\\ {h}^{-2}\nabla \zeta \left({t}_{N}\right)\end{array}\right]=\frac{1}{{h}^{2}}\left[\begin{array}{cccccc}1& 0& 0& 0& \cdots & 0\\ -2& 1& 0& 0& \cdots & 0\\ 1& -2& 1& 0& \cdots & 0\\ \cdots & \cdots & \cdots & \ddots & \cdots & \cdots \\ 0& \cdots & 1& -2& 1& 0\\ 0& 0& \cdots & 1& -2& 1\end{array}\right]\left[\begin{array}{c}{\zeta }_{0}\\ {\zeta }_{1}\\ {\zeta }_{2}\\ \vdots \\ {\zeta }_{N-1}\\ {\zeta }_{N}\end{array}\right]$$

(A.4)

The matrix form of $q$-th integer-order derivative can be computed as:

$$\left[\begin{array}{c}{h}^{-q}{\nabla }^{q}\zeta \left({t}_{0}\right)\\ {h}^{-q}{\nabla }^{q}\zeta \left({t}_{1}\right)\\ {h}^{-q}{\nabla }^{q}\zeta \left({t}_{2}\right)\\ \vdots \\ {h}^{-q}{\nabla }^{q}\zeta \left({t}_{N-1}\right)\\ {h}^{-q}{\nabla }^{q}\zeta \left({t}_{N}\right)\end{array}\right]=\frac{1}{{h}^{q}}\left[\begin{array}{cccccc}{\beta }_{0}^{\left(q\right)}& 0& 0& 0& \cdots & 0\\ {\beta }_{1}^{\left(q\right)}& {\beta }_{0}^{\left(q\right)}& 0& 0& \cdots & 0\\ {\beta }_{2}^{\left(q\right)}& {\beta }_{1}^{\left(q\right)}& {\beta }_{0}^{\left(q\right)}& 0& \cdots & 0\\ \cdots & \cdots & \cdots & \ddots & \cdots & \cdots \\ {\beta }_{N-1}^{\left(q\right)}& \cdots & {\beta }_{2}^{\left(q\right)}& {\beta }_{1}^{\left(q\right)}& {\beta }_{0}^{\left(q\right)}& 0\\ {\beta }_{N}^{\left(q\right)}& {\beta }_{N-1}^{\left(q\right)}& \cdots & {\beta }_{2}^{\left(q\right)}& {\beta }_{1}^{\left(q\right)}& {\beta }_{0}^{\left(q\right)}\end{array}\right]\left[\begin{array}{c}{\zeta }_{0}\\ {\zeta }_{1}\\ {\zeta }_{2}\\ \vdots \\ {\zeta }_{N-1}\\ {\zeta }_{N}\end{array}\right]$$

(A.5)

$${\beta }_{i}^{\left(q\right)}={\left(-1\right)}^{i}\left(\genfrac{}{}{0pt}{}{q}{i}\right), \quad i=\mathrm{0,1},\dots ,N.$$

(A.6)

Similarly, the triangular strip matrix can also be applied for the derivative of the real order. Here, the left-sided fractional derivative of fractional order $\alpha$ of the function $\zeta \left(t\right)$ can be written as:

$$\frac{{d}^{\alpha }}{{dt}^{\alpha }}\zeta \left(t\right)=\frac{1}{\Gamma \left(1-\alpha \right)}\frac{d}{{dt}}{\int }_{a}^{b}\frac{\zeta \left(\uptau \right)d\tau }{{\left(t-\uptau \right)}^{\alpha }} ,\quad a<t<b$$

(A.7)

Using the backward fractional difference approximation for the $\alpha$-th derivative at the interval points ${t}_{p, }p=\mathrm{1,2},\dots ,N$ can be computed as:

$$\frac{{d}^{\alpha }}{{dt}^{\alpha }}\zeta \left(t\right)\approx \frac{{\nabla }^{\alpha }\zeta \left({t}_{p}\right)}{{h}^{\alpha }}=\frac{1}{{h}^{\alpha }}\sum_{i=0}^{p}{\left(-1\right)}^{i}\left(\genfrac{}{}{0pt}{}{\alpha }{i}\right){\zeta }_{p-i },\quad p=\mathrm{0,1},\dots ,N.$$

(A.8)

The matrix form of $\alpha$-th order derivative can be represented as:

$$\left[\begin{array}{c}{h}^{-\alpha }{\nabla }^{\alpha }\zeta \left({t}_{0}\right)\\ {h}^{-\alpha }{\nabla }^{\alpha }\zeta \left({t}_{1}\right)\\ {h}^{-\alpha }{\nabla }^{\alpha }\zeta \left({t}_{2}\right)\\ \vdots \\ {h}^{-\alpha }{\nabla }^{\alpha }\zeta \left({t}_{N-1}\right)\\ {h}^{-\alpha }{\nabla }^{\alpha }\zeta \left({t}_{N}\right)\end{array}\right]=\frac{1}{{h}^{\alpha }}\left[\begin{array}{cccccc}{\beta }_{0}^{\left(\alpha \right)}& 0& 0& 0& \cdots & 0\\ {\beta }_{1}^{\left(\alpha \right)}& {\beta }_{0}^{\left(\alpha \right)}& 0& 0& \cdots & 0\\ {\beta }_{2}^{\left(\alpha \right)}& {\beta }_{1}^{\left(\alpha \right)}& {\beta }_{0}^{\left(\alpha \right)}& 0& \cdots & 0\\ \cdots & \cdots & \cdots & \ddots & \cdots & \cdots \\ {\beta }_{N-1}^{\left(\alpha \right)}& \cdots & {\beta }_{2}^{\left(\alpha \right)}& {\beta }_{1}^{\left(\alpha \right)}& {\beta }_{0}^{\left(\alpha \right)}& 0\\ {\beta }_{N}^{\left(\alpha \right)}& {\beta }_{N-1}^{\left(\alpha \right)}& \cdots & {\beta }_{2}^{\left(\alpha \right)}& {\beta }_{1}^{\left(\alpha \right)}& {\beta }_{0}^{\left(\alpha \right)}\end{array}\right]\left[\begin{array}{c}{\zeta }_{0}\\ {\zeta }_{1}\\ {\zeta }_{2}\\ \vdots \\ {\zeta }_{N-1}\\ {\zeta }_{N}\end{array}\right] ;$$

(A.9)

$${\beta }_{i}^{\left(\alpha \right)}={\left(-1\right)}^{i}\left(\genfrac{}{}{0pt}{}{\alpha }{i}\right),\quad i=\mathrm{0,1},\dots ,N.,$$

(A.10)

Step 3: Make the system matrix for the entire differential equation including the right-hand side.

Step 4: Apply zero initial conditions, i.e., we have to remove the rows and columns corresponding to that initial conditions. For the non-zero initial conditions, an auxiliary function is used to make the problem with zero initial conditions (Podlubny 2000).

Step 5: Solve the linear algebraic equations to get numerical solutions.

The accuracy of this approach purely depends on the step size h, i.e., a smaller step size leads to higher accuracy.