Analytical bending solutions of thin plates with two adjacent edges free and the others clamped or simply supported using finite integral transform method

Abstract

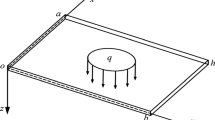
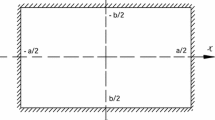
The finite integral transform method is developed to explore the bending analysis of thin plates with the combination of simply supported, clamped, and free boundary conditions. Previous solutions mostly focused on simply supported and clamped boundary conditions, but the existence of free boundary conditions makes the solving process more complex, because it is difficult to find the exact solution which satisfies both deflection and internal force by conventional inverse/semi-inverse method or approximate method. Using this method, the plate high-order partial differential equation is simplified to a linear algebraic equation by the integral transformation. Then, through some mathematical manipulation, the analytical solution is elegantly achieved in a straightforward procedure. Compared with other methods, the present method is much simpler and general and does not need to pre-determine the deflection function, which makes it very attractive for calculating the mechanical responses of the plates. Comprehensive analytical results obtained in this paper illuminate the validity of the proposed method by comparison with the existing literature and finite-element method using (ABAQUS) software.

Appendix: detailed derivation for the transformation of each term in Eq. (1).

$$ \begin{gathered} \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial^{4} W}}{{\partial x^{4} }}} } \sin \frac{{\alpha_{m} x}}{2}\sin \frac{{\beta_{n} y}}{2}{\text{d}}x{\text{d}} y{\kern 1pt} {\kern 1pt} \hfill \\ = \int_{0}^{b} {\sin \frac{{\beta_{n} y}}{2}\left[ {\left. {\left( {\frac{{\partial^{3} W}}{{\partial x^{3} }}\sin \frac{{\alpha_{m} x}}{2}} \right)} \right|_{x = 0}^{x = a} - \frac{{\alpha_{m} }}{2}\int_{0}^{a} {\frac{{\partial^{3} W}}{{\partial x^{3} }}\cos \frac{{\alpha_{m} x}}{2}{\text{d}}x} } \right]} {\text{d}} y \hfill \\ = \int_{0}^{b} {\sin \frac{{\beta_{n} y}}{2}\left[ {\left. {\left( {\frac{{\partial^{3} W}}{{\partial x^{3} }}\sin \frac{{\alpha_{m} x}}{2}} \right)} \right|_{x = 0}^{x = a} - \frac{{\alpha_{m} }}{2}\left. {\left( {\frac{{\partial^{2} W}}{{\partial x^{2} }}\cos \frac{{\alpha_{m} x}}{2}} \right)} \right|_{x = 0}^{x = a} - \left( {\frac{{\alpha_{m} }}{2}} \right)^{2} \int_{0}^{a} {\frac{{\partial^{2} W}}{{\partial x^{2} }}\sin \frac{{\alpha_{m} x}}{2}{\text{d}}x} } \right]} {\text{d}} y \hfill \\ = \int_{0}^{b} {\sin \frac{{\beta_{n} y}}{2}\left[ \begin{gathered} \left. {\left( {\frac{{\partial^{3} W}}{{\partial x^{3} }}\sin \frac{{\alpha_{m} x}}{2}} \right)} \right|_{x = 0}^{x = a} - \frac{{\alpha_{m} }}{2}\left. {\left( {\frac{{\partial^{2} W}}{{\partial x^{2} }}\cos \frac{{\alpha_{m} x}}{2}} \right)} \right|_{x = 0}^{x = a} \hfill \\ - \left( {\frac{{\alpha_{m} }}{2}} \right)^{2} \left. {\left( {\frac{\partial W}{{\partial x}}\sin \frac{{\alpha_{m} x}}{2}} \right)} \right|_{x = 0}^{x = a} + \left( {\frac{{\alpha_{m} }}{2}} \right)^{3} \int_{0}^{a} {\frac{\partial W}{{\partial x}}\cos \frac{{\alpha_{m} x}}{2}{\text{d}}x} \hfill \\ \end{gathered} \right]} {\text{d}} y \hfill \\ = \int_{0}^{b} {\left[ \begin{gathered} \left. {\left( {\frac{{\partial^{3} W}}{{\partial x^{3} }}\sin \frac{{\alpha_{m} x}}{2}} \right)} \right|_{x = 0}^{x = a} - \frac{{\alpha_{m} }}{2}\left. {\left( {\frac{{\partial^{2} W}}{{\partial x^{2} }}\cos \frac{{\alpha_{m} x}}{2}} \right)} \right|_{x = 0}^{x = a} \hfill \\ - \left( {\frac{{\alpha_{m} }}{2}} \right)^{2} \left. {\left( {\frac{\partial W}{{\partial x}}\sin \frac{{\alpha_{m} x}}{2}} \right)} \right|_{x = 0}^{x = a} + \left. {\left( {\frac{{\alpha_{m} }}{2}} \right)^{3} \left( {W\cos \frac{{\alpha_{m} x}}{2}} \right)} \right|_{x = 0}^{x = a} \hfill \\ \end{gathered} \right]\sin \frac{{\beta_{n} y}}{2}} {\text{d}} y \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \left( {\frac{{\alpha_{m} }}{2}} \right)^{4} \int_{0}^{a} {\int_{0}^{b} {W\sin \frac{{\alpha_{m} x}}{2}\sin \frac{{\beta_{n} y}}{2}} } {\text{d}}x{\text{d}} y \hfill \\ = \left( {\frac{{\alpha_{m} }}{2}} \right)^{4} W_{mn} + \int_{0}^{b} {\left[ \begin{gathered} \left( { - 1} \right)^{{\frac{m - 1}{2}}} \left. {\frac{{\partial^{3} W}}{{\partial x^{3} }}} \right|_{x = a} + \left. {\frac{{\alpha_{m} }}{2}\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right|_{x = 0} \hfill \\ - \left. {\left( { - 1} \right)^{{\frac{m - 1}{2}}} \left( {\frac{{\alpha_{m} }}{2}} \right)^{2} \frac{\partial W}{{\partial x}}} \right|_{x = a} - \left. {\left( {\frac{{\alpha_{m} }}{2}} \right)^{3} W} \right|_{x = 0} \hfill \\ \end{gathered} \right]} \sin \frac{{\beta_{n} y}}{2}{\text{d}} y, \hfill \\ \end{gathered} $$

$$ \begin{gathered} \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial^{4} W}}{{\partial y^{4} }}} } \sin \frac{{\alpha_{m} x}}{2}\sin \frac{{\beta_{n} y}}{2}{\text{d}}x{\text{d}} y{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ = \int_{0}^{a} {\sin \frac{{\alpha_{m} x}}{2}\left[ {\left. {\left( {\frac{{\partial^{3} W}}{{\partial y^{3} }}\sin \frac{{\beta_{n} y}}{2}} \right)} \right|_{y = 0}^{y = b} - \frac{{\beta_{n} }}{2}\int_{0}^{b} {\frac{{\partial^{3} W}}{{\partial y^{3} }}\cos \frac{{\beta_{n} y}}{2}{\text{d}} y} } \right]} {\text{d}}x{\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ = \int_{0}^{a} {\sin \frac{{\alpha_{m} x}}{2}\left[ {\left. {\left( {\frac{{\partial^{3} W}}{{\partial y^{3} }}\sin \frac{{\beta_{n} y}}{2}} \right)} \right|_{y = 0}^{y = b} - \frac{{\beta_{n} }}{2}\left. {\left( {\frac{{\partial^{2} W}}{{\partial y^{2} }}\cos \frac{{\beta_{n} y}}{2}} \right)} \right|_{y = 0}^{y = b} - \left( {\frac{{\beta_{n} }}{2}} \right)^{2} \int_{0}^{b} {\frac{{\partial^{2} W}}{{\partial y^{2} }}\sin \frac{{\beta_{n} y}}{2}{\text{d}} y} } \right]} {\text{d}}x{\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ = \int_{0}^{a} {\sin \frac{{\alpha_{m} x}}{2}\left[ \begin{gathered} \left. {\left( {\frac{{\partial^{3} W}}{{\partial y^{3} }}\sin \frac{{\beta_{n} y}}{2}} \right)} \right|_{y = 0}^{y = b} - \frac{{\beta_{n} }}{2}\left. {\left( {\frac{{\partial^{2} W}}{{\partial y^{2} }}\cos \frac{{\beta_{n} y}}{2}} \right)} \right|_{y = 0}^{y = b} \hfill \\ - \left( {\frac{{\beta_{n} }}{2}} \right)^{2} \left. {\left( {\frac{\partial W}{{\partial y}}\sin \frac{{\beta_{n} y}}{2}} \right)} \right|_{y = 0}^{y = b} + \left( {\frac{{\beta_{n} }}{2}} \right)^{3} \int_{0}^{b} {\frac{\partial W}{{\partial y}}\cos \frac{{\beta_{n} y}}{2}{\text{d}} y} \hfill \\ \end{gathered} \right]} {\text{d}}x{\kern 1pt} {\kern 1pt} \hfill \\ = \int_{0}^{a} {\left[ \begin{gathered} \left. {\left( {\frac{{\partial^{3} W}}{{\partial y^{3} }}\sin \frac{{\beta_{n} y}}{2}} \right)} \right|_{y = 0}^{y = b} - \frac{{\beta_{n} }}{2}\left. {\left( {\frac{{\partial^{2} W}}{{\partial y^{2} }}\cos \frac{{\beta_{n} y}}{2}} \right)} \right|_{y = 0}^{y = b} \hfill \\ - \left( {\frac{{\beta_{n} }}{2}} \right)^{2} \left. {\left( {\frac{\partial W}{{\partial y}}\sin \frac{{\beta_{n} y}}{2}} \right)} \right|_{y = 0}^{y = b} + \left( {\frac{{\beta_{n} }}{2}} \right)^{3} \left. {\left( {W\cos \frac{{\beta_{n} y}}{2}} \right)} \right|_{y = 0}^{y = b} \hfill \\ \end{gathered} \right]\sin \frac{{\alpha_{m} x}}{2}} {\text{d}}x \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \left( {\frac{{\beta_{n} }}{2}} \right)^{4} \int_{0}^{a} {\int_{0}^{b} W } \sin \frac{{\alpha_{m} x}}{2}\sin \frac{{\beta_{n} y}}{2}{\text{d}}x{\text{d}} y \hfill \\ = \left( {\frac{{\beta_{n} }}{2}} \right)^{4} W_{mn} + \int_{0}^{a} {\left[ \begin{gathered} \left( { - 1} \right)^{{\frac{n - 1}{2}}} \left. {\frac{{\partial^{3} W}}{{\partial y^{3} }}} \right|_{y = b} + \frac{{\beta_{n} }}{2}\left. {\frac{{\partial^{2} W}}{{\partial y^{2} }}} \right|_{y = 0} \hfill \\ - \left( { - 1} \right)^{{\frac{n - 1}{2}}} \left( {\frac{{\beta_{n} }}{2}} \right)^{2} \left. {\frac{\partial W}{{\partial y}}} \right|_{y = b} - \left. {\left( {\frac{{\beta_{n} }}{2}} \right)^{3} W} \right|_{y = 0} \hfill \\ \end{gathered} \right]} \sin \frac{{\alpha_{m} x}}{2}{\text{d}} x. \hfill \\ \end{gathered} $$

Integration by parts on $\frac{{\partial^{4} W}}{{\partial x^{2} \partial y^{2} }}$ with considering the x variable first:

$$ \begin{gathered} \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial^{4} W}}{{\partial x^{2} \partial y^{2} }}} } \sin \frac{{\alpha_{m} x}}{2}\sin \frac{{\beta_{n} y}}{2}{\text{d}} x{\text{d}} y{\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ = \int_{0}^{b} {\sin \frac{{\beta_{n} y}}{2}} \left[ {\left. {\left( {\frac{{\partial^{3} W}}{{\partial x\partial y^{2} }}\sin \frac{{\alpha_{m} x}}{2}} \right)} \right|_{x = 0}^{x = a} - \frac{{\alpha_{m} }}{2}\int_{0}^{a} {\frac{{\partial^{3} W}}{{\partial x\partial y^{2} }}\cos \frac{{\alpha_{m} x}}{2}{\text{d}} x} } \right]{\text{d}} y{\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ = \int_{0}^{b} {\sin \frac{{\beta_{n} y}}{2}} \left[ {\left. {\left( {\frac{{\partial^{3} W}}{{\partial x\partial y^{2} }}\sin \frac{{\alpha_{m} x}}{2}} \right)} \right|_{x = 0}^{x = a} - \frac{{\alpha_{m} }}{2}\left. {\left( {\frac{{\partial^{2} W}}{{\partial y^{2} }}\cos \frac{{\alpha_{m} x}}{2}} \right)} \right|_{x = 0}^{x = a} } \right]{\text{d}} y \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\frac{{\alpha_{m} }}{2}} \right)^{2} \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial^{2} W}}{{\partial y^{2} }}} } \sin \frac{{\alpha_{m} x}}{2}\sin \frac{{\beta_{n} y}}{2}{\text{d}} x{\text{d}} y{\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ = \int_{0}^{b} {\left[ {\left. {\left( {\frac{{\partial^{3} W}}{{\partial x\partial y^{2} }}\sin \frac{{\alpha_{m} x}}{2}} \right)} \right|_{x = 0}^{x = a} - \frac{{\alpha_{m} }}{2}\left. {\left( {\frac{{\partial^{2} W}}{{\partial y^{2} }}\cos \frac{{\alpha_{m} x}}{2}} \right)} \right|_{x = 0}^{x = a} } \right]} \sin \frac{{\beta_{n} y}}{2}{\text{d}} y \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \left( {\frac{{\alpha_{m} }}{2}} \right)^{2} \int_{0}^{a} {\left[ {\left. {\left( {\frac{\partial W}{{\partial y}}\sin \frac{{\beta_{n} y}}{2}} \right)} \right|_{y = 0}^{y = b} - \left. {\frac{{\beta_{n} }}{2}\left( {W\cos \frac{{\beta_{n} y}}{2}} \right)} \right|_{y = 0}^{y = b} } \right]} \sin \frac{{\alpha_{m} x}}{2}{\text{d}} x \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \left( {\frac{{\alpha_{m} }}{2}} \right)^{2} \left( {\frac{{\beta_{n} }}{2}} \right)^{2} \int_{0}^{a} {\int_{0}^{b} W } \sin \frac{{\alpha_{m} x}}{2}\sin \frac{{\beta_{n} y}}{2}{\text{d}} x{\text{d}} y \hfill \\ = \left( {\frac{{\alpha_{m} }}{2}} \right)^{2} \left( {\frac{{\beta_{n} }}{2}} \right)^{2} W_{mn} + \int_{0}^{b} {\left[ {\left( { - 1} \right)^{{\frac{m - 1}{2}}} \left. {\frac{{\partial^{3} W}}{{\partial x\partial y^{2} }}} \right|_{x = a} + \frac{{\alpha_{m} }}{2}\left. {\frac{{\partial^{2} W}}{{\partial y^{2} }}} \right|_{x = 0} } \right]} \sin \frac{{\beta_{n} y}}{2}{\text{d}} y \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \left( {\frac{{\alpha_{m} }}{2}} \right)^{2} \int_{0}^{a} {\left[ {\left( { - 1} \right)^{{\frac{n - 1}{2}}} \left. {\frac{\partial W}{{\partial y}}} \right|_{y = b} + \left. {\frac{{\beta_{n} }}{2}W} \right|_{y = 0} } \right]} \sin \frac{{\alpha_{m} x}}{2}{\text{d}} x. \hfill \\ \end{gathered} $$

Integration by parts on $\frac{{\partial^{4} W}}{{\partial x^{2} \partial y^{2} }}$ with considering the y variable first:

$$ \begin{gathered} \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial^{4} W}}{{\partial x^{2} \partial y^{2} }}} } \sin \frac{{\alpha_{m} x}}{2}\sin \frac{{\beta_{n} y}}{2}{\text{d}} x{\text{d}} y{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ = \int_{0}^{a} {\sin \frac{{\alpha_{m} x}}{2}\left[ {\left. {\left( {\frac{{\partial^{3} W}}{{\partial x^{2} \partial y}}\sin \frac{{\beta_{n} y}}{2}} \right)} \right|_{y = 0}^{y = b} - \frac{{\beta_{n} }}{2}\int_{0}^{b} {\frac{{\partial^{3} W}}{{\partial x^{2} \partial y}}\cos \frac{{\beta_{n} y}}{2}{\text{d}} y} } \right]} {\kern 1pt} {\text{d}} x{\kern 1pt} {\kern 1pt} \hfill \\ = \int_{0}^{a} {\sin \frac{{\alpha_{m} x}}{2}\left[ {\left. {\left( {\frac{{\partial^{3} W}}{{\partial x^{2} \partial y}}\sin \frac{{\beta_{n} y}}{2}} \right)} \right|_{y = 0}^{y = b} - \frac{{\beta_{n} }}{2}\left. {\left( {\frac{{\partial^{2} W}}{{\partial x^{2} }}\cos \frac{{\beta_{n} y}}{2}} \right)} \right|_{y = 0}^{y = b} } \right]} {\kern 1pt} {\text{d}} x \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - {\kern 1pt} \left( {\frac{{\beta_{n} }}{2}} \right)^{2} \int_{0}^{a} {\int_{0}^{b} {\frac{{\partial^{2} W}}{{\partial x^{2} }}} } \sin \frac{{\alpha_{m} x}}{2}\sin \frac{{\beta_{n} y}}{2}{\text{d}} x{\text{d}} y{\kern 1pt} \hfill \\ = \int_{0}^{a} {\left[ {\left. {\left( {\frac{{\partial^{3} W}}{{\partial x^{2} \partial y}}\sin \frac{{\beta_{n} y}}{2}} \right)} \right|_{y = 0}^{y = b} - \frac{{\beta_{n} }}{2}\left. {\left( {\frac{{\partial^{2} W}}{{\partial x^{2} }}\cos \frac{{\beta_{n} y}}{2}} \right)} \right|_{y = 0}^{y = b} } \right]} \sin \frac{{\alpha_{m} x}}{2}{\text{d}} x \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \left( {\frac{{\beta_{n} }}{2}} \right)^{2} \int_{0}^{b} {\left[ {\left. {\left( {\frac{\partial W}{{\partial x}}\sin \frac{{\alpha_{m} x}}{2}} \right)} \right|_{x = 0}^{x = a} - \left. {\frac{{\alpha_{m} }}{2}\left( {W\cos \frac{{\alpha_{m} x}}{2}} \right)} \right|_{x = 0}^{x = a} } \right]} \sin \frac{{\beta_{n} y}}{2}{\text{d}} y \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \left( {\frac{{\alpha_{m} }}{2}} \right)^{2} \left( {\frac{{\beta_{n} }}{2}} \right)^{2} \int_{0}^{a} {\int_{0}^{b} W } \sin \frac{{\alpha_{m} x}}{2}\sin \frac{{\beta_{n} y}}{2}{\text{d}} x{\text{d}} y{\kern 1pt} {\kern 1pt} \hfill \\ = \left( {\frac{{\alpha_{m} }}{2}} \right)^{2} \left( {\frac{{\beta_{n} }}{2}} \right)^{2} W_{mn} + \int_{0}^{a} {\left[ {\left( { - 1} \right)^{{\frac{n - 1}{2}}} \left. {\frac{{\partial^{3} W}}{{\partial x^{2} \partial y}}} \right|_{y = b} + \frac{{\beta_{n} }}{2}\left. {\frac{{\partial^{2} W}}{{\partial x^{2} }}} \right|_{y = 0} } \right]} \sin \frac{{\alpha_{m} x}}{2}{\text{d}} x \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \left( {\frac{{\beta_{n} }}{2}} \right)^{2} \int_{0}^{b} {\left[ {\left( { - 1} \right)^{{\frac{m - 1}{2}}} \left. {\frac{\partial W}{{\partial x}}} \right|_{x = a} + \left. {\frac{{\alpha_{m} }}{2}W} \right|_{x = 0} } \right]} \sin \frac{{\beta_{n} y}}{2}{\text{d}} y. \hfill \\ \end{gathered} $$