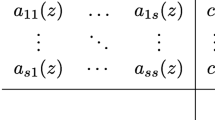Skip to main content
Springer Nature Link
Log in

Highly stable multistep Runge–Kutta methods for Volterra integral equations

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

Abstract

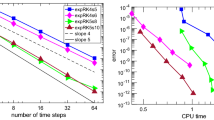
In this paper, we investigate highly stable multistep Runge–Kutta methods for Volterra integral equations. First, the order conditions for order p and stage order \(q=p\) are presented, and a convergence theorem is given. The numerical stability conditions for the basic and convolution test equations are derived. Then, the methods with one or two stages are studied in detail. Some A-stable and \(V_0\)-stable m-stage methods with order \(p>m\) are obtained. For one-stage methods, we also construct \(A_0\)-stable and -stable methods of orders 3 and 4. Finally, numerical experiments are given to confirm the theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  • Abdi A (2019) General linear methods with large stability regions for Volterra integral equations. Comput. Appl. Math. 38(2):52, 16

    Article  MathSciNet  MATH  Google Scholar 

  • Baker CTH, Keech MS (1978) Stability regions in the numerical treatment of Volterra integral equations. SIAM J. Numer. Anal. 15(2):394–417

    Article  MathSciNet  MATH  Google Scholar 

  • Bellen A, Jackiewicz Z, Vermiglio R, Zennaro M (1989) Natural continuous extensions of Runge–Kutta methods for Volterra integral equations of the second kind and their applications. Math. Comp. 52(185):49–63

    Article  MathSciNet  MATH  Google Scholar 

  • Bellen A, Jackiewicz Z, Vermiglio R, Zennaro M (1990) Stability analysis of Runge-Kutta methods for Volterra integral equations of the second kind. IMA J. Numer. Anal. 10(1):103–118

    Article  MathSciNet  MATH  Google Scholar 

  • Brunner H (2004) Collocation methods for Volterra integral and related functional differential equations. Cambridge University Press, Cambridge

    Book  MATH  Google Scholar 

  • Brunner H, Hairer E, Nørsett SP (1982) Runge–Kutta theory for Volterra integral equations of the second kind. Math. Comp. 39(159):147–163

    Article  MathSciNet  MATH  Google Scholar 

  • Brunner H, Nørsett SP, Wolkenfelt PH (1980) On \(V_{0}\)-stability of numerical methods for Volterra integral equations of the second kind. Afdeling Numerieke Wiskunde [Department of Numerical Mathematics], 84. Mathematisch Centrum, Amsterdam

  • Butcher JC (2008) Numerical methods for ordinary differential equations, 2nd edn. Wiley, Chichester

    Book  MATH  Google Scholar 

  • Chen Y, Li X, Tang T (2013) A note on Jacobi spectral-collocation methods for weakly singular Volterra integral equations with smooth solutions. J. Comput. Math. 31(1):47–56

    Article  MathSciNet  MATH  Google Scholar 

  • Conte D, D’Ambrosio R, Izzo G, Jackiewicz Z (2014) Natural Volterra Runge–Kutta methods. Numer. Algorithms 65(3):421–445

    Article  MathSciNet  MATH  Google Scholar 

  • Conte D, Jackiewicz Z, Paternoster B (2008) Two-step almost collocation methods for Volterra integral equations. Appl. Math. Comput. 204(2):839–853

    MathSciNet  MATH  Google Scholar 

  • Conte D, Paternoster B (2009) Multistep collocation methods for Volterra integral equations. Appl. Numer. Math. 59(8):1721–1736

    Article  MathSciNet  MATH  Google Scholar 

  • Fazeli S, Hojjati G, Shahmorad S (2012) Super implicit multistep collocation methods for nonlinear Volterra integral equations. Math. Comput. Modelling 55(3–4):590–607

    Article  MathSciNet  MATH  Google Scholar 

  • Garrappa R (2010) Order conditions for Volterra Runge–Kutta methods. Appl. Numer. Math. 60(5):561–573

    Article  MathSciNet  MATH  Google Scholar 

  • Hairer E, Lubich C, Nørsett SP (1983) Order of convergence of one-step methods for Volterra integral equations of the second kind. SIAM J. Numer. Anal. 20(3):569–579

    Article  MathSciNet  MATH  Google Scholar 

  • Hosseini SA, Abdi A (2016) On the numerical stability of the linear barycentric rational quadrature method for Volterra integral equations. Appl. Numer. Math. 100:1–13

    Article  MathSciNet  MATH  Google Scholar 

  • Izzo G, Jackiewicz Z, Messina E, Vecchio A (2010) General linear methods for Volterra integral equations. J. Comput. Appl. Math. 234(9):2768–2782

    Article  MathSciNet  MATH  Google Scholar 

  • Izzo G, Russo E, Chiapparelli C (2012) Highly stable Runge–Kutta methods for Volterra integral equations. Appl. Numer. Math. 62(8):1002–1013

    Article  MathSciNet  MATH  Google Scholar 

  • Jackiewicz Z (2009) General linear methods for ordinary differential equations. Wiley, Hoboken

    Book  MATH  Google Scholar 

  • Lambert JD (1973) Computational methods in ordinary differential equations. Wiley, London-New York-Sydney

    MATH  Google Scholar 

  • Li M, Huang C (2019) The linear barycentric rational quadrature method for auto-convolution Volterra integral equations. J. Sci. Comput. 78(1):549–564

    Article  MathSciNet  MATH  Google Scholar 

  • Li M, Huang C, Ming W (2019) Barycentric rational collocation methods for Volterra integral equations with weakly singular kernels. Comput. Appl. Math. 38(3):120, 15

    MathSciNet  MATH  Google Scholar 

  • Li Y, Yang Z, Zhang C (2019) Theoretical and numerical analysis of third-kind auto-convolution Volterra integral equations. Comput. Appl. Math. 38(4):170, 17

    MathSciNet  MATH  Google Scholar 

  • Liang H, Brunner H (2019) The convergence of collocation solutions in continuous piecewise polynomial spaces for weakly singular Volterra integral equations. SIAM J. Numer. Anal. 57(4):1875–1896

    Article  MathSciNet  MATH  Google Scholar 

  • Linz P (1985) Analytical and numerical methods for Volterra equations. SIAM, Philadelphia

    Book  MATH  Google Scholar 

  • Zhang L, Ma F (2015) Pouzet–Runge–Kutta-Chebyshev method for Volterra integral equations of the second kind. J. Comput. Appl. Math. 288:323–331

    Article  MathSciNet  MATH  Google Scholar 

  • Zhang R, Liang H, Brunner H (2016) Analysis of collocation methods for generalized auto-convolution Volterra integral equations. SIAM J. Numer. Anal. 54(2):899–920

    Article  MathSciNet  MATH  Google Scholar 

  • Zhao J, Long T, Xu Y (2019) Multistep collocation methods for Volterra integral equations with weakly singular kernels. East Asian J. Appl. Math. 9(1):67–86

    Article  MathSciNet  Google Scholar 

  • Zhao J, Long T, Xu Y (2019) Super implicit multistep collocation methods for weakly singular Volterra integral equations. Numer. Math. Theory Methods Appl. 12(4):1039–1065

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors are very grateful to the anonymous referees and the editors for their valuable suggestions and comments.

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Huazhong University of Science and Technology, Wuhan, 430074, China

    Jiao Wen & Chengming Huang

  2. School of Mathematics and Computational Science & Hunan Key Laboratory for Computation and Simulation in Science and Engineering, Xiangtan University, Hunan, 411105, China

    Aiguo Xiao

  3. Hubei Key Laboratory of Engineering Modeling and Scientific Computing, Huazhong University of Science and Technology, Wuhan, 430074, China

    Chengming Huang

Authors
  1. Jiao Wen
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Aiguo Xiao
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Chengming Huang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Chengming Huang.

Ethics declarations

Funding information

This work was supported by National Natural Science Foundation of China (Nos. 11771163, 12011530058 and 12071403).

Additional information

Communicated by Hui Liang.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wen, J., Xiao, A. & Huang, C. Highly stable multistep Runge–Kutta methods for Volterra integral equations. Comp. Appl. Math. 39, 308 (2020). https://doi.org/10.1007/s40314-020-01351-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-020-01351-z

Keywords

Mathematics Subject Classification