Skip to main content
Springer Nature Link
Log in

Numerical solution of Bratu’s and related problems using a third derivative hybrid block method

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

Abstract

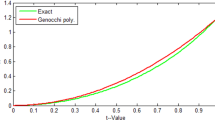
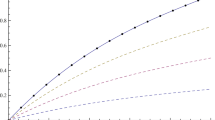
A new one-step hybrid block method with third derivatives and optimized features aimed at solving the classical one-dimensional Bratu’s and Reactor design problems is developed. The development of the new method considers three intermediate points that are properly chosen through the optimization of the local truncation errors corresponding to the main formulas to approximate the solution and the first derivative at the end point of the block, and another approximation of the solution at an intermediate point. The convergence analysis and the order of the proposed method are analyzed. Some specific problems are solved to demonstrate the efficiency and feasibility of the technique adopted. The numerical results provided through the implementation of the scheme are very much closer to the exact solutions and are found favorably compared with different methods in the available literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  • Abd-el-Malek MB, Abdelrazek A, Ghazy M, Gamal G (2019) A modified perturbation solution to the one-dimensional Bratu problem. Appl Math Comput 354:296–304

    MathSciNet  MATH  Google Scholar 

  • Boyd JP (2001) Chebyshev and Fourier spectral methods. Courier Corporation, Chelmsford

    MATH  Google Scholar 

  • Buckmire R (2004) Application of a Mickens finite-difference scheme to the cylindrical Bratu-Gelfand problem. Numer Methods Partial Diff Equ 20:327–337

    Article  MathSciNet  Google Scholar 

  • Caglar H, Caglar N, Ozer M, Valaristos A, Anagnostopoulos AN (2010) B-spline method for solving Bratu’s problem. Int J Comput Math 87(8):1885–1891

    Article  MathSciNet  Google Scholar 

  • Canuto C, Hussaini MY, Quarteroni A, Zang TA (1988) Spectral methods in fluid dynamics. Springer, New York

    Book  Google Scholar 

  • Chawla M, Subramanian R, Sathi HL (1988) A fourth order method for a singular two-point boundary value problem. BIT 28:88–97

    Article  MathSciNet  Google Scholar 

  • Das N, Singh R, Wazwaz AM, Kumar J (2016) An algorithm based on the variational iteration technique for the Bratu-type and the Lane-Emden problems. J Math Chem 54(2):527–551

    Article  MathSciNet  Google Scholar 

  • Gray BF (1978) The distribution of heat sources in the human head-theoretical consideration. J Theor Biol 71:255–263

    Article  Google Scholar 

  • Jacobsen J, Schmitt K (2002) The Liouville-Bratu-Gelfand problem for radial operators. J Diff Equ 184:283–298

    Article  MathSciNet  Google Scholar 

  • Kafri HQ, Khuri SA (2016) Bratus problem: a novel approach using fixed-point iterations and Greens functions. Comput Phys Commun 198:97–104

    Article  MathSciNet  Google Scholar 

  • Khuri SA (2004) A new approach to Bratu’s problem. Appl Math Comput 147:131–136

    MathSciNet  MATH  Google Scholar 

  • Mohsen A (2014) A simple solution of the Bratu problem. Comput Math Appl 67:26–33

    Article  MathSciNet  Google Scholar 

  • Na TY (1979) Computational methods in engineering boundary value problems. Academic Press, New York, pp 181–184

    Google Scholar 

  • Pandey PK (2010) Finite difference method for a second-order ordinary differential equation with a boundary condition of the third kind. Comput Methods Appl Math 10(1):109–116

    Article  MathSciNet  Google Scholar 

  • Ramos H, Rufai MA (2019a) Numerical solution of boundary value problems by using an optimized two-step block method. Numer Algorithms. https://doi.org/10.1007/s11075-019-00753-3

    Article  MATH  Google Scholar 

  • Ramos H, Rufai MA (2019b) A third-derivative two-step block Falkner-type method for solving general second-order boundary-value systems. Math Comput Simul 165:139–155

    Article  MathSciNet  Google Scholar 

  • Roul P, Madduri H (2019) An optimal iterative algorithm for solving Bratu-type problems. J Math Chem 57:583–598

    Article  MathSciNet  Google Scholar 

  • Rufai MA, Ramos H (2020) One-step hybrid block method containing third derivatives and improving strategies for solving Bratu’s and Troesch’s problems. Num Math: Theor, Methods Appl 13:946–972

    MathSciNet  Google Scholar 

  • Temimi H (2012) A discontinuous Galerkin finite element method for solving the Troeschs problem. Appl Math Comput 219:521–529

    MathSciNet  MATH  Google Scholar 

  • Wan Y, Guo Q, Pan N (2004) Thermo-electro-hydrodynamic model for electro-spinning process. Int J Nonlinear Sci Numer Simul 5:5–8

    Google Scholar 

  • Wazwaz AM (2005) Adomian decomposition method for a reliable treatment of the Bratu-type equations. Appl Math Comput 166:652–663

    MathSciNet  MATH  Google Scholar 

  • Zahoor Raja MA, Samar R, Alaidarous ES, Shivanian E (2016) Bio-inspired computing platform for reliable solution of Bratu-type equations arising in the modeling of electrically conducting solids. Appl Math Model 40(11–12):5964–5977

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Dipartimento di Matematica, Università degli Studi di Bari Aldo Moro, Via Orabona 4, 70125, Bari, Italy

    M. A. Rufai

  2. Scientific Computing Group, Universidad de Salamanca, Plaza de la Merced, 37008, Salamanca, Spain

    Higinio Ramos

  3. Escuela Politécnica Superior de Zamora, Campus Viriato, 49022, Zamora, Spain

    Higinio Ramos

Authors
  1. M. A. Rufai
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Higinio Ramos
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to M. A. Rufai.

Additional information

Communicated by Jose Alberto Cuminato.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rufai, M.A., Ramos, H. Numerical solution of Bratu’s and related problems using a third derivative hybrid block method. Comp. Appl. Math. 39, 322 (2020). https://doi.org/10.1007/s40314-020-01372-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-020-01372-8

Keywords

Mathematics Subject Classification

Profiles

  1. M. A. Rufai View author profile
  2. Higinio Ramos View author profile