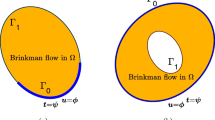
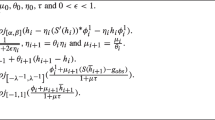Abstract
This paper is devoted to the numerical resolution of an inverse Cauchy problem governed by Stokes equation modeling the airflow in the lungs. It consists in determining the air velocity and pressure on the artificial boundaries of the bronchial tree. This data completion problem is one of the highly ill-posed problems in the Hadamard sense (Hadamard in Lectures on Cauchy’s problem in linear partial differential equations. Dover, New York, 1953). This gives great importance to its numerical resolution and in particular to carry out stable numerical approaches, mostly in the case of noisy data. The main idea of this work is to extend some regularizing, stable and fast iterative algorithms for solving this problem based on the domain decomposition approach (Chakib et al. in Inverse Prob 35(1):015008, 2018). We discuss the efficiency and the feasibility of the proposed approach through some numerical tests performed using different domain decomposition algorithms. Finally, we opt for the Robin–Robin algorithm, which showed its performance, for the numerical simulation of the airflow in the bronchial tree configuration.






























Similar content being viewed by others
References
Abda AB, Saad IB, Hassine M (2013) Recovering boundary data: the Cauchy stokes system. Appl Math Model 37(1–2):1–12
Aboulaich R, Abda AB, Kallel M (2013) A control type method for solving the Cauchy–Stokes problem. Appl Math Model 37(6):4295–4304
Agusti A, Noguera A, Sauleda J, Sala E, Pons J, Busquets X (2003) Systemic effects of chronic obstructive pulmonary disease. Eur Respir J 21(2):347–360
Alves CJ, Silvestre A (2004) Density results using stokeslets and a method of fundamental solutions for the Stokes equations. Eng Anal Boundary Elem 28(10):1245–1252
Andrieux S, Baranger T, Abda AB (2006) Solving Cauchy problems by minimizing an energy-like functional. Inverse Prob 22(1):115
Arnold DN, Brezzi F, Fortin M (1984) A stable finite element for the Stokes equations. Calcolo 21(4):337–344
Awan FG, Saleem O, Kiran A (2019) Recent trends and advances in solving the inverse problem for EEG source localization. Inverse Probl Sci Eng 27(11):1521–1536
Bastay G, Johansson T, Kozlov VA, Lesnic D (2006) An alternating method for the stationary Stokes system. ZAMM J Appl Math Mech/Zeitschrift für Angewandte Mathematik und Mechanik: Applied Mathematics and Mechanics 86(4):268–280
Belgacem FB (2007) Why is the cauchy problem severely ill-posed? Inverse Prob 23(2):823
Ben Belgacem F, El Fekih H (2005) On Cauchy’s problem: I. A variational Steklov–Poincaré theory. Inverse Prob 21(6):1915
Berntsson F, Kozlov VA, Mpinganzima L, Turesson BO (2014) An accelerated alternating procedure for the Cauchy problem for the Helmholtz equation. Comput Math Appl 68(1):44–60
Berntsson F, Kozlov VA, Mpinganzima L, Turesson B-O (2017) Iterative Tikhonov regularization for the Cauchy problem for the Helmholtz equation. Comput Math Appl 73(1):163–172
Boffi D, Brezzi F, Fortin M et al (2013) Mixed finite element methods and applications, vol 44. Springer, Berlin
Bourgeois L, Chesnel L (2020) On quasi-reversibility solutions to the cauchy problem for the laplace equation: regularity and error estimates. ESAIM Math Model Num Anal 54(2):493–529
Bourgeois L, Dardé J (2010) A duality-based method of quasi-reversibility to solve the Cauchy problem in the presence of noisy data. Inverse Prob 26(9):095016
Caubet F, Dardé J, Godoy M (2019) On the data completion problem and the inverse obstacle problem with partial Cauchy data for laplace’s equation. ESAIM Control Optim Calc Var 25:30
Chakib A, Nachaoui A, Nachaoui M, Ouaissa H (2018) On a fixed point study of an inverse problem governed by stokes equation. Inverse Prob 35(1):015008
Chen B, Sun Y, Zhuang Z (2019) Method of fundamental solutions for a Cauchy problem of the Laplace equation in a half-plane. Boundary Value Problems 2019(1):34
Chen C, Young D, Tsai C, Murugesan K (2005) The method of fundamental solutions for inverse 2d Stokes problems. Comput Mech 37(1):2–14
Cheng X, Gong R, Han W (2016) A coupled complex boundary method for the Cauchy problem. Inverse Prob Sci Eng 24(9):1510–1527
Cimetiere A, Delvare F, Jaoua M, Pons F (2001) Solution of the Cauchy problem using iterated Tikhonov regularization. Inverse Prob 17(3):553
Clason C, Klibanov MV (2008) The quasi-reversibility method for thermoacoustic tomography in a heterogeneous medium. SIAM J Sci Comput 30(1):1–23
Cotes JE, Chinn DJ, Miller MR (2009) Lung function: physiology, measurement and application in medicine. Wiley, Hoboken
Dardé J (2016) Iterated quasi-reversibility method applied to elliptic and parabolic data completion problems. Inverse Prob Imaging 10
Deimling K (2010) Nonlinear functional analysis. Courier Corporation
Delvare F, Cimetière A, Hanus J-L, Bailly P (2010) An iterative method for the cauchy problem in linear elasticity with fading regularization effect. Comput Methods Appl Mech Eng 199(49–52):3336–3344
Egloffe A-C (2012) Etude de quelques problemes inverses pour le systeme de Stokes. Application aux poumons. PhD thesis, Citeseer
Fairweather G, Karageorghis A (1998) The method of fundamental solutions for elliptic boundary value problems. Adv Comput Math 9(1–2):69
Fan C-M, Li P-W (2015) Numerical solutions of direct and inverse stokes problems by the method of fundamental solutions and the laplacian decomposition. Num Heat Transfer Part B Fund 68(3):204–223
Feng X-L, Fu C-L, Cheng H (2011) A regularization method for solving the Cauchy problem for the Helmholtz equation. Appl Math Model 35(7):3301–3315
García GC, Montoya C, Osses A (2017) A source reconstruction algorithm for the stokes system from incomplete velocity measurements. Inverse Prob 33(10):105003
Grech R, Cassar T, Muscat J, Camilleri KP, Fabri SG, Zervakis M, Xanthopoulos P, Sakkalis V, Vanrumste B (2008) Review on solving the inverse problem in EEG source analysis. J Neuroeng Rehab 5(1):25
Grisvard P (2011) Elliptic problems in nonsmooth domains, volume 69 of Classics in Applied Mathematics. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA (2011) Reprint of the 1985 original [MR0775683]. With a foreword by Susanne C, Brenner
Hadamard J (1953) Lectures on Cauchy’s problem in linear partial differential equations. Dover, New York
Hadj A, Saker H (2020) Integral equations method for solving a biharmonic inverse problem in detection of robin coefficients. Appl Num Math
Hariga-Tlatli N, Baranger T, Erhel J (2010) Misfit functional for recovering data in 2d electrocardiography problems. Eng Anal Boundary Elem 34(5):492–500
Hecht F, Le Hyaric A, Ohtsuka K, Pironneau O (2011) Freefem++, finite elements software
Johansson BT, Lesnic D, Reeve T (2011) A comparative study on applying the method of fundamental solutions to the backward heat conduction problem. Math Comput Modell 54(1–2):403–416
Jourhmane M, Nachaoui A (1999) An alternating method for an inverse Cauchy problem. Num Algorithms 21(1–4):247
Kalinin A, Potyagaylo D, Kalinin V (2019) Solving the inverse problem of electrocardiography on the endocardium using a single layer source. Front Physiol 10:58
Karageorghis A, Lesnic D, Marin L (2012) The method of fundamental solutions for the detection of rigid inclusions and cavities in plane linear elastic bodies. Comput Struct 106:176–188
Klibanov MV (2006) Estimates of initial conditions of parabolic equations and inequalities via lateral Cauchy data. Inverse Prob 22(2):495
Klibanov MV (2013) Thermoacoustic tomography with an arbitrary elliptic operator. Inverse Prob 29(2):025014
Klibanov MV (2015) Carleman estimates for the regularization of ill-posed Cauchy problems. Appl Num Math 94:46–74
Kozlov VA, Maz’Ya VG, Fomin AV (1991) An iterative method for solving the Cauchy problem for elliptic equations. Comput Maths Math Phys 31(1):45–52
Lai R-Y, Uhlmann G, Wang J-N (2015) Inverse boundary value problem for the stokes and the Navier–Stokes equations in the plane. Arch Ration Mech Anal 215(3):811–829
Lattés R, Lions JL (1969) The method of quasi-reversibility: applications to partial differential equations. Elsevier, New York
Lechleiter A, Rienmüller T (2013) Factorization method for the inverse stokes problem. Inverse Problems Imaging 7(4):1271
Lesnic D, Elliott L, Ingham D, Zeb A (1999) A numerical method for an inverse biharmonic problem. Inverse Probl Eng 7(5):409–431
Li J, Guo BL (2013) The quasi-reversibility method to solve the Cauchy problems for parabolic equations. Acta Math Sin 29(8):1617–1628
Marin L (2010) An alternating iterative MFS algorithm for the Cauchy problem for the modified Helmholtz equation. Comput Mech 45(6):665–677
Marin L, Cipu C (2017) Non-iterative regularized MFS solution of inverse boundary value problems in linear elasticity: a numerical study. Appl Math Comput 293:265–286
Onyango T, Ingham DB, Lesnic D (2009) Inverse reconstruction of boundary condition coefficients in one-dimensional transient heat conduction. Appl Math Comput 207(2):569–575
Onyango T, Ingham DB, Lesnic D (2009) Reconstruction of boundary condition laws in heat conduction using the boundary element method. Comput Math Appl 57(1):153–168
Polak AG (1998) A forward model for maximum expiration. Comput Biol Med 28(6):613–625
Qin H, Wen D (2008) Tikhonov type regularization method for the Cauchy problem of the modified Helmholtz equation. Appl Math Comput 203(2):617–628
Qin H-H, Wei T (2009) Quasi-reversibility and truncation methods to solve a Cauchy problem for the modified helmholtz equation. Math Comput Simul 80(2):352–366
Quarteroni A, Valli A (1999) Domain decomposition methods for partial differential equations. Oxford University Press, Oxford
Richardson LF (1911) Ix. the approximate arithmetical solution by finite differences of physical problems involving differential equations, with an application to the stresses in a masonry dam. Philos Trans R Soc Lond Ser A Contain Papers Math Phys Char, 210(459-470):307–357
Rischette R, Baranger T, Debit N (2014) Numerical analysis of an energy-like minimization method to solve a parabolic Cauchy problem with noisy data. J Comput Appl Math 271:206–222
Tikhonov AN, Arsenin VI, John F (1977) Solutions of ill-posed problems, vol 14. Winston Washington, DC
Xiao X, Wang X, Yin H (2019) Preconditioned Richardson iteration for augmented linear systems. Num Algorithms 82(3):843–867
Yang JP, Chen Y-C (2020) Gradient enhanced localized radial basis collocation method for inverse analysis of cauchy problems. Int J Appl Mech
Yang JP, Guan P-C, Fan C-M (2016) Weighted reproducing kernel collocation method and error analysis for inverse Cauchy problems. Int J Appl Mech 8(03):1650030
Yang JP, Guan P-C, Fan C-M (2017) Solving inverse Laplace equation with singularity by weighted reproducing kernel collocation method. Int J Appl Mech 9(05):1750065
Yang JP, Hsin W-C (2019) Weighted reproducing kernel collocation method based on error analysis for solving inverse elasticity problems. Acta Mech 230(10):3477–3497
Yang JP, Lin Q et al (2020) Investigation of multiply connected inverse cauchy problems by efficient weighted collocation method. Int J Appl Mech 12(1)
Yeih W-C, Chan I-Y, Ku C-Y, Fan C-M (2015) Solving the inverse Cauchy problem of the Laplace equation using the method of fundamental solutions and the exponentially convergent scalar homotopy algorithm (ecsha). J Mar Sci Technol 23(2):162–171
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Antonio José Silva Neto.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
About this article
Cite this article
Chakib, A., Ouaissa, H. On numerical resolution of an inverse Cauchy problem modeling the airflow in the bronchial tree. Comp. Appl. Math. 40, 27 (2021). https://doi.org/10.1007/s40314-021-01420-x
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40314-021-01420-x