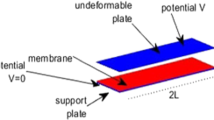
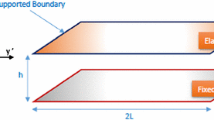
Abstract
As known, a 1D membrane MEMS semi-linear elliptic model with fringing field can be written as
where \(\lambda ^2\) and \(\delta \) are positive parameters and u is the deflection of the membrane. Since the electric field \( {\mathbf {E}} \) on the membrane is locally orthogonal to the straight tangent line to the membrane, \(|{\mathbf {E}}|\) can be considered locally proportional to the curvature K of the membrane, so that a well-known model with fringing field in which \(|{\mathbf {E}}|^2\propto \lambda ^2/(1-u)^2\) has been here considered. In this paper, starting from this model, we present a new algebraic condition of uniqueness for the solution of this model depending on the electromechanical properties of the material constituting the membrane, which weighs more than the condition of existence known in literature. Furthermore, shooting-Dekker–Brent, Keller-Box-scheme, and III/IV Stage Lobatto IIIA formulas were exploited and their performances compared to recover u under convergence conditions in the presence/absence of ghost solutions. Finally, a criterion that is able to choose the material constituting the membrane starting from the applied electric voltage V and vice versa, in conditions of convergence, and in the presence and absence of ghost solutions, is presented.






Similar content being viewed by others
Notes
Again, this continuity protects us from dangerous tears in the membrane profile.
Obviously, V must also satisfy (67).
References
Ali IA (2012) Modeling and simulation of MEMS components: challenges and possible solutions. Micromachining techniques for fabrication o micro and nano structures. Springer Nature, Singapore
Angiulli G, Jannelli A, Morabito FC, Versaci M (2018) Recondtruting the membrane detection of a 1\(D\) electrostatic-driven MEMS device by the shooting method: convergence analysis and ghost solutions identification. Comput Appl Math 37:4484–4498. https://doi.org/10.1007/s40314-017-0564-4
Batra RC, Porfiri M, Spinello D (2006) Electromechanical model of electrically actuated narrow microbeams. J Microelectromech Syst 15(5):1175–1189
Batra RC, Porfiri M, Spinello D (2006) Micro Nano Lett 1:2
Batra RC, Porfiri M, Spinello D (2007) Review of modeling electrostatically actuated microelectromechanical systems. Smart Mater Struct 16:6
Bayley PB, Shampine LF, Waltman PE (1969) Nonlinear two points boundary value problems. Academic Press, New York
Bechtold T, Schrag G, Feng L (2013) System-level modeling of MEMS. Wiley, London
Cassani D, Tarsia A (2016) Periodic solutions to nonlocal MEMS equations. Discret Contin Dyn Syst Ser S 9(3):631–642
Cassani D, d’O M, Ghoussoub N (2009) On a fourth order elliptic problem with a singular nonlinearity. Nonlinear Stud 9:189–209
Cassani D, Fattorusso L, Tarsia A (2014) Nonlocal dynamic problems with singular nonlinearities and application to MEMS. Nonlinear Differ Equ Appl 85:185–206
Cassani D, Fattorusso L, Tarsia A (2013) Nonlocal singular problems and application to MEMS. In: Proceedings of world congress on engineering, pp 155–164
Cauchi M et al (2018) Analytical, numerical and experimental study of a horizontal electrothermal MEMS microgripper of the deformability charcterization of human red blood cells. Micromachines 9(3):108–119
Chen YX et al (2019) Fringing field effect analysis of parallel plate capacitors for capacitive power transfer application. In: Proceedings of 4th IEEE international future energy electronics conference, pp 115–120
de Oliveira Hansen R et al (2018) Magnetic films for electromagnetic actuation ibn MEMS switches. Microsyst Technol 24:10
Di Barba P, Wiak S (2020) MEMS: field models and optimal design. Springer, Berlin
Di Barba P, Fattorusso L, Versaci M (2017) Electrostatic field in terms of geometric curvature in membrane MEMS devices. Commun Appl Ind Math 8(1):165–184
Di Barba P, Gotsalk T, Majastrzyk W, Mognaschi M, Orlowska K (2018) Optimal design of electromagnetically actuated MEMS cantilevers. Sensors 18(8):25–33
Di Barba P, Fattorusso L, Versaci M (2019) A 2\(D\) non-linear second-order differential model for electrostatic circular membrane MEMS devices: a result of existence and uniqueness. Mathematics 7(1193):1–18
Di Barba P, Fattorusso L, Versaci M (2020) Curvature dependent electrostatic field in the deformable MEMS device: stability and optimal control. Commun Appl Ind Math 11(1):35–54
Di Barba P, Fattorusso L, Versaci M (2021) Curvature-dependent electrostatic field as a principle for modelling membrane MEMS device with fringing field. Comput Appl Math 40(3):87
Farokhi H, Ghayesh MH (2017) Nonlinear thermo-mechanical behaviour of MEMS resonators. Microsyst Technol 23:5303–5315
Fento J, Liu C, Zhang W, Hao S (2018) Static and dynamic mechanical behaviors of electrostatic MEMS resonator with surface processing error. Micromach MDPI 9(34):1–29
Gad-el-Hak M (2006) MEMS: design and fabrication. Chapman & Hall, New York
Gallalgher E, Moussa W (2014) A study of the effect of the fringing fields on the electrostatic force in vertical comb drives. Sensors 1:20149–20164
Howell LL, Luon SM (2004) Thermomechanical in-plane microactuator (TIM), U.S. Patent N. 6
Javaheri H, Ghanati PP, Azizi S (2018) A case study on the numerical solution and reduced order model of MEMS. Sens MDPI 19:3
Leus V, Elata V (2004) Fringing field effect in electrostatic actuator. Technical Report ETR-2004-2
Mistry KK, Mahapatra A (2012) Design and simulation of a thermo-transfer type MEMS based micro flow sensor for arterial blood flow measurement. Microsyst Technol 18(6):683–692
Mohammad TF, Oukad HM (2016) Static, eigenvalue problem and bifurcation analysis of MEMS arches actuated by electrostatic fringing-fields. Microsyst Technol 22:193–206
Mohammadi A, Ali N (2015) Effect of high electrostatic actuation on thermoelastic damping in thin rectangular microplate resonators. J Theoret Appl Mech 53(2):317–3209
Nathanson H, Newell W, Wickstrom R, Lewis J (1964) The resonant gate transistor. IEEE Trans Electron Devices 14:117–133
Oukad HM (2014) Static response and natural frequencies of microbeams actuated by out-of-plane electrostatic fringing-fields. Int J Non-Linear Mech 62:39–48
Oukad HM (2018) Electrostatic fringing-fields effects on the structural behavior of MEMS shallow arches. Microsyst Technol 24:1391–1399
Pelesko JA, Bernstein DH (2003) Modeling MEMS and NEMS. CRC Press, Boca Raton
Pelesko JA, Driscoll TA (2005) The effect of the small-aspect-ratio approximation on canonical electrostatic MEMS models. J Eng Math 53:239–252
Quarteroni A, Sacco R, Saleri F (2007) Numerical mathematics. Springer, Berlin
Ren Z et al (2020) Thermo-mechanical modeling and experimental validation for multilayered metallic microstructures. Microsyst Technol 21:751–783
Velosa-Moncada L et al (2018) Design of a novel MEMS microgripper with rotatory electrostatic combdrive actuators for biomedical applications. Sensors 18(15):1–16
Versaci M, Morabito FC (2019) Membrane micro electro-mechanical systems for industrial applications, handbook of research on advanced mechatronic systems and intelligent. Robotics 20:139–175
Versaci M, Angiulli G, Fattoryusso L, Jannelli A (2019) On the uniqueness of the solution for a semi-linear elliptic boundary value problem of the membrane MEMS device for the recostructing the membrane profile in absence of ghost solutions. Int J Non-Linear Mech 109:24–31
Versaci M, Di Barba P, Morabito FC (2020) Curvature-dependent electrostatic field as a principle for modelling membrane-based MEMS devices. A review. Membr MDPI 10(11):1–51
Versaci M, Jannelli A, Angiulli G (2020) Electrostatic Micro-Electromechanical-Systems (MEMS) Devices: a Comparison Among Numerical techniques for recovering the membrane profile. IEEE Access 8:125874–125886
Vinyas M, Kattimani S (2018) Investigation of the Effect of \(BaTiO_3-CoFe_{24}\) Particle Arrangement on the Static Response of magneto-electro-thermo-elastic plates. Compos Struct 185:51–56
Wei J, Ye D (2010) On MEMS equation with fringing field. Proc Am Math Soc 138(2):1693–1699
Weng CC, Kong JA (1980) Effects of fringing fields on the capacitance of circular microstrip disk. IEEE Trans Microw Theory Tech 28(2):98–104
Yu Y et al (2012) Numerical and analytical approximations to large post-buckling deformation of MEMS. Int J Mech Sci 55(1):95–103
Zega V, Frang A, Guercilena A (2018) Analysis of frequency stability and thermoelastic effects for slotted tuning fork MEMS resonators. Sensors 8(7):1–15
Zhang Y et al (2018) Micro electrostatic energy harvester with both broad bandwidth and high normalized power density. Appl Energy 212:363–371
Zhao X et al (2004) A reduced-order model for electrically actuated microplates. J Micromech Microeng 14:7
Zozulya VV, Saez A (2016) A high-order theory of a thermoelastic beams and its application to the MEMS/NEMS analysis and simulations. Arch Appl Mech 86:1255–1273
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by José R Fernández.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Versaci, M., Barba, P.D. & Morabito, F.C. MEMS with fringing field: curvature-dependent electrostatic field and numerical techniques for recovering the membrane profile. Comp. Appl. Math. 40, 128 (2021). https://doi.org/10.1007/s40314-021-01519-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40314-021-01519-1
Keywords
- MEMS devices
- Fringing field
- BVP semi-linear elliptic problems
- Shooting and Keller-Box scheme
- III/IV stage/Lobatto IIIA formulaes