Skip to main content
SpringerLink
Log in

Numerical simulations of reaction–diffusion systems in biological and chemical mechanisms with quartic-trigonometric B-splines

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

Abstract

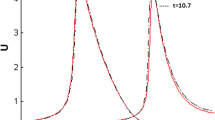
This article concerns with the numerical investigations of the reaction–diffusion systems (RDSs) arising in the study of pattern formation in biological and chemical systems with the employment of the quartic-trigonometric B-spline functions. The computationally numerical scheme uses collocation method which is established by a relatively new B-splines for the spatial discretizations and, for time integration Crank–Nicolson technique is adapted. Therefore, solutions of the RDSs are assembled by the wholly discretized space-time scheme. A matrix stability analysis is performed for the numerical scheme after linearization process. Experimental cases include Brusselator model, Gray–Scott model, Schnakenberg model as well as a linear problem in one-dimensional domain. Numerical solutions are compared to the existing studies. Spatial pattern formation is demonstrated by present computational algorithm.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  • Abbas M, Majid AA, Ismail AIM, Rashid A (2014a) The application of cubic trigonometric B-spline to the numerical solution of the hyperbolic problems. Appl Math Comput 239:74–88

    MathSciNet  MATH  Google Scholar 

  • Abbas M, Majid AA, Ismail AIM, Rashid A (2014b) Numerical method using cubic trigonometric B-spline technique for nonclassical diffusion problems. Abstr Appl Anal. https://doi.org/10.1155/2014/849682

    Article  MathSciNet  MATH  Google Scholar 

  • Alinia N, Zarebnia M (2018) Trigonometric tension B-spline method for the solution of problems in calculus of variations. Comput Math Math Phys 58(5):631–641. https://doi.org/10.1134/S0965542518050020

    Article  MathSciNet  MATH  Google Scholar 

  • Alinia N, Zarebnia M (2019) A numerical algorithm based on a new kind of tension B-spline function for solving Burgers–Huxley equation. Numer Algorithms 82:1121–1142

    Article  MathSciNet  Google Scholar 

  • Chaplain MA, Ganesh M, Graham IG (2001) Spatio-temporal pattern formation on spherical surfaces: numerical simulation and application to solid tumour growth. J Math Biol 42(5):387–423. https://doi.org/10.1007/s002850000067

    Article  MathSciNet  MATH  Google Scholar 

  • Chivukula V, Mousel J, Lu J, Vigmostad S (2014) Micro-scale blood particulate dynamics using a non-uniform rational B-spline-based isogeometric analysis. Int J Numer Methods Biomed Eng 30(12):1437–1459

    Article  Google Scholar 

  • Chou CS, Zhang YT, Zhao R, Nie Q (2007) Numerical methods for stiff reaction–diffusion systems. Discrete Contin Dyn Syst B 7(3):515–525

    Article  MathSciNet  Google Scholar 

  • Colli Franzone P, Pavarino LF (2004) A parallel solver for reaction–diffusion systems in computational electrocardiology. Math Models Methods Appl Sci 14(06):883–911. https://doi.org/10.1142/S0218202504003489

    Article  MathSciNet  MATH  Google Scholar 

  • Daba IT, Duressa GF (2020) Extended cubic B-spline collocation method for singularly perturbed parabolic differential–difference equation arising in computational neuroscience. Int J Numer Methods Biomed Eng. https://doi.org/10.1002/cnm.3418

    Article  Google Scholar 

  • Dag I, Hepson OE (2021) Hyperbolic-trigonometric tension B-spline Galerkin approach for the solution of Fisher equation. AIP Conf Proc AIP Publ LLC 2334(1):090004

    Article  Google Scholar 

  • Dag I, Hepson OE (2021) Hyperbolic-trigonometric tension B-spline Galerkin approach for the solution of RLW equation. AIP Conf Proc AIP Publ LLC 2334(1):090005

    Article  Google Scholar 

  • Ersoy Hepson O (2021) Numerical simulations of Kuramoto–Sivashinsky equation in reaction–diffusion via Galerkin method. Math Sci. https://doi.org/10.1007/s40096-021-00402-8

    Article  MathSciNet  Google Scholar 

  • Ersoy O, Dag I (2015) Numerical solutions of the reaction diffusion system by using exponential cubic B-spline collocation algorithms. Open Phys 13:414–427

    Article  Google Scholar 

  • Ghorai S, Poria S (2016) Turing patterns induced by cross-diffusion in a predator–prey system in presence of habitat complexity. Chaos Solitons Fractals 91:421–429. https://doi.org/10.1016/j.chaos.2016.07.003

    Article  MathSciNet  MATH  Google Scholar 

  • Hepson OE, Yiğit G (2021) Numerical investigations of physical processes for regularized long wave equation. In: Allahviranloo T, Salahshour S, Arica N (eds) Progress in intelligent decision science. IDS 2020. Advances in intelligent systems and computing, vol 1301. Springer, Cham, pp 710–724. https://doi.org/10.1007/978-3-030-66501-2_58

    Chapter  Google Scholar 

  • Hepson OE (2020) A quartic trigonometric tension b-spline algorithm for nonlinear partial differential equation system. Eng Comput. https://doi.org/10.1108/EC-05-2020-0289

    Article  Google Scholar 

  • Hepson OE, Dag I (2019) Finite element method for schnakenberg model. Mathematical methods in engineering. Nonlinear systems and complexity. Springer, Cham, pp 41–51. https://doi.org/10.1007/978-3-319-90972-1_3

    Book  Google Scholar 

  • Hoogendoorn C, Sebastian R, Rodriguez JF, Lekadir K, Frangi AF (2017) An atlas-and data-driven approach to initializing reaction–diffusion systems in computer cardiac electrophysiology. Int J Numer Methods Biomed Eng 33(8):e2846. https://doi.org/10.1002/cnm.2846

    Article  Google Scholar 

  • Jain MK (1983) Numerical solution of differential equations, 2nd edn. Wiley, New York

    Google Scholar 

  • Korkmaz A, Ersoy O, Dag I (2017) Motion of patterns modeled by the Gray–Scott autocatalysis system in one dimension. Commun Math Comput Chem 77:507–526

    MathSciNet  Google Scholar 

  • Lengyel I, Epstein IR (1992) A chemical approach to designing Turing patterns in reaction–diffusion systems. Proc Natl Acad Sci 89(9):3977–3979

    Article  Google Scholar 

  • Madzvamuse A, Chung AH (2016) The bulk-surface finite element method for reaction–diffusion systems on stationary volumes. Finite Elem Anal Des 108:9–21

    Article  Google Scholar 

  • Madzvamuse A, Maini PK (2007) Velocity-induced numerical solutions of reaction–diffusion systems on continuously growing domains. J Comput Phys 225(1):100–119. https://doi.org/10.1016/j.jcp.2006.11.022

    Article  MathSciNet  MATH  Google Scholar 

  • Madzvamuse A, Gaffney EA, Maini PK (2010) Stability analysis of non-autonomous reaction–diffusion systems: the effects of growing domains. J Math Biol 61(1):133–164

    Article  MathSciNet  Google Scholar 

  • Mittal RC, Rohila R (2016) Numerical simulation of reaction–diffusion systems by modified cubic B-spline differential quadrature method. Chaos Solitons Fractals 92:9–19

    Article  MathSciNet  Google Scholar 

  • Onarcan AT, Adar N, Dag I (2018) Trigonometric cubic B-spline collocation algorithm for numerical solutions of reaction–diffusion equation systems. Comput Appl Math 37(5):6848–6869

    Article  MathSciNet  Google Scholar 

  • Ozugurlu E (2015) A note on the numerical approach for the reaction–diffusion problem to model the density of the tumor growth dynamics. Comput Math Appl 69(12):1504–1517

    Article  MathSciNet  Google Scholar 

  • Sahin A (2009) Numerical solutions of the reaction-diffusion equations with B-spline finite element method. Ph.D. Thesis. Turkey: Doctoral dissertation. Department of Mathematics. Eskişehir Osmangazi University, Eskisehir

  • Sarfaraz W, Madzvamuse A (2018) Domain-dependent stability analysis of a reaction–diffusion model on compact circular geometries. Int J Bifurc Chaos 28(08):1830024

    Article  MathSciNet  Google Scholar 

  • Sarfaraz W, Madzvamuse A (2020) Stability analysis and parameter classification of a reaction–diffusion model on an annulus. J Appl Nonlinear Dyn 9(4):589–617

    Article  MathSciNet  Google Scholar 

  • Schnakenberg J (1979) Simple chemical reaction systems with limit cycle behaviour. J Theor Biol 81:389–400

    Article  MathSciNet  Google Scholar 

  • Silva-Dias L, Lopez-Castillo A (2020) Turing patterns modulation by chemical gradient in isothermal and non-isothermal conditions. Phys Chem Chem Phys 22(14):7507–7515

    Article  Google Scholar 

  • Tok-Onarcan A, Adar N, Dag I (2019) Wave simulations of Gray–Scott reaction–diffusion system. Math Methods Appl Sci 42(16):5566–5581

    Article  MathSciNet  Google Scholar 

  • Turing AM (1952) The chemical basis of morphogenesis. Philos Trans R Soc Lond Ser B Biol Sci 237:37–72. https://doi.org/10.1098/rstb.1952.0012

    Article  MathSciNet  MATH  Google Scholar 

  • Wang G, Fang M (2008) Unified and extended form of three types of splines. J Comput Appl Math 216(2):498–508

    Article  MathSciNet  Google Scholar 

  • Ya-Juan L, Guo-Zhao W (2005) Two kinds of B-basis of the algebraic hyperbolic space. J Zhejiang Univ Sci A 6(7):750–759. https://doi.org/10.1631/jzus.2005.A0750

    Article  Google Scholar 

  • Zhang R, Yu X, Zhu J, Loula AF (2014) Direct discontinuous Galerkin method for nonlinear reaction–diffusion systems in pattern formation. Appl Math Model 38(5–6):1612–1621

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics and Computer Science, Faculty of Science and Letters, Eskisehir Osmangazi University, Eskişehir, Turkey

    Ozlem Ersoy Hepson

  2. Department of Mathematics, Faculty of Engineering and Natural Sciences, Bahcesehir University, Istanbul, Turkey

    Gülsemay Yiğit & Tofigh Allahviranloo

Authors
  1. Ozlem Ersoy Hepson
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Gülsemay Yiğit
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Tofigh Allahviranloo
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All persons who meet authorship criteria are listed as authors, and all authors certify that they have participated sufficiently in the work to take public responsibility for the content, including participation in the concept, design, analysis, writing, or revision of the manuscript. Furthermore, each author certifies that this material or similar material has not been and will not be submitted to or published in any other publication.

Corresponding author

Correspondence to Tofigh Allahviranloo.

Ethics declarations

Conflict of interest

No conflict of interest exists. We wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.

Additional information

Communicated by Baisheng Yan.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hepson, O.E., Yiğit, G. & Allahviranloo, T. Numerical simulations of reaction–diffusion systems in biological and chemical mechanisms with quartic-trigonometric B-splines. Comp. Appl. Math. 40, 144 (2021). https://doi.org/10.1007/s40314-021-01524-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-021-01524-4

Keywords

Mathematics Subject Classification

Search

Navigation