Abstract
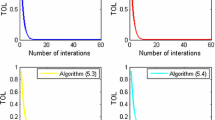
In this paper, we modified the shrinking projection method with the parallel monotone hybrid method for approximating common fixed points of a finite family of G-nonexpansive mappings. We then prove a strong convergence theorem under suitable conditions in Hilbert spaces endowed with graphs. Moreover, we give some numerical examples and compare the rate of convergence of our algorithms. Finally, we provide an application to signal recovery in a situation without knowing the type of noises and demonstrate the computational performance of our algorithm in comparison to some methods. The numerical results of the comparative analysis are also discussed.










Similar content being viewed by others
References
Aleomraninejad SMA, Rezapour S, Shahzad N (2012) Some fixed point results on a metric space with a graph. Topology Appl 159:659–663
Alfuraidan MR (2015) On monotone Ciric quasi-contraction mappings with a graph. Fixed Point Theory Appl 2015:93
Alfuraidan MR, Khamsi MA (2015) Fixed points of monotone nonexpansive mappings on a hyperbolic metric space with a graph. Fixed Point Theory Appl 2015:44
Anh PK, Hieu DV (2015) Parallel and sequential hybrid methods for a finite family of asymptotically quasi \(\phi \)-nonexpansive mappings. J Appl Math Comput 48:241–263
Anh PK, Hieu DV (2015) Parallel hybrid methods for variational inequalities, equilibrium problems and common fixed point problem. Math Viet J. https://doi.org/10.1007/s10013-015-0129-z
Berinde V (2002) Iterative approximation of fixed points. Baia Mare, Roumania, Editura efemeride, p 1
Burden RL, Faires JD (2010) Numerical analysis, 9th edn. Brooks/Cole-Cengage Learning, Boston
Cholamjiak P, Suantai S, Sunthrayuth P (2019) An explicit parallel algorithm for solving variational inclusion problem and fixed point problem in Banach space. Math Anal Banach J. https://doi.org/10.1007/s43037-019-00030-4
Chaolamjiak W, Yambangwai D, Hammad HA (2020) Modified Hybrid Projection Methods with SP Iterations for Quasi-Nonexpansive Multivalued Mappings in Hilbert Spaces. Bull Iran Math Soc: 1–24
Hieu DV (2017) Parallel and cyclic hybrid subgradient extragradient methods for variational inequalities. Afrika Mat. 28:677–692
Jachymski J (2008) The contraction principle for mappings on a metric space with a graph. Proc Am Math Soc 136:1359–1373
Khan SA, Suantai S, Cholamjiak W (2019) Shrinking projection methods involving inertial forward-backward splitting methods for inclusion problems. Revista de la Real Academia de Ciencias Exactas, Fisicas y Naturales Serie A Matematicas 113(2):645–656
Kitkuan D, Kumam P, Martinez-Moreno J, Sitthithakerngkiet K (2020) Inertial viscosity forward-backward splitting algorithm for monotone inclusions and its application to image restoration problems. Int J Comput Math 97:482–497
Kankam K, Pholasa N, Cholamjiak P (2019) On convergence and complexity of the modified forward-backward method involving new linesearches for convex minimization. Math Methods Appl Sci 42:1352–1362
Marino G, Xu HK (2007) Weak and strong convergence theorems for strict pseudo-contractions in Hilbert spaces. J Math Anal Appl 329:336–346
Nakajo K, Takahashi W (2003) Strong convergence theorems for nonexpansive mappings and nonexpansive semigroups. J Math Anal Appl 279:372–379
Phuengrattana W, Suantai S (2011) On the rate of convergence of Mann, Ishikawa, Noor and Ss-iterations for continuous functions on an arbitrary interval. J Comput Appl Math 235:3006–3014
Rhoades BE (1976) Comments on two fixed point iteration methods. J Math Anal Appl 56:741–750
Sridarat P, Suparaturatorn R, Suantai S, Cho YJ (2019) Convergence analysis of Ss-iteration for G-nonexpansive mappings with directed graphs. Bull Malays Math Sci Soc 42:2361–2380
Stoi M, Xavier J, Dodig M (2016) Projection on the intersection of convex sets. Linear Algebra Appl 509:191–205
Suantai S, Donganont M, Cholamjiak W (2019) Hybrid methods for a countable family of g-nonexpansive mappings in hilbert spaces endowed with graphs. Mathematics 7:936
Suantai S, Kankam K, Cholamjiak P (2020) A Novel forward-backward algorithm for solving convex minimization problem in hilbert spaces. Mathematics 8:42
Suparatulatorn R, Suantai S, Cholamjiak W (2017) Hybrid methods for a finite family of G-nonexpansive mappings in Hilbert spaces endowed with graphs. AKCE Int J Graphs Comb 14:101–111
Tiammee J, Kaewkhao A, Suantai S (2015) On Browder’s convergence theorem and Halpern iteration process for G-nonexpansive mappings in Hilbert spaces endowed with graphs. Fixed Point Theory Appl 1:187
Tripak O (2016) Common fixed points of G-nonexpansive mappings on Banach spaces with a graph. Fixed Point Theory Appl 1:87
Van Hieu D (2015) A parallel hybrid method for equilibrium problems, variational inequalities and nonexpansive mappings in Hilbert space. J Korean Math Soc 52:373–388
Van Hieu D (2017) Parallel hybrid methods for generalized equilibrium problems and asymptotically strictly pseudocontractive mappings. J Appl Math Comput 53:531–554
Van Hieu D, Anh PK (2016) Parallel hybrid extragradient methods for pseudomonotone equilibrium problems and nonexpansive mappings. Numer Algorithms 73:197–217
Van Hieu D, Cho YJ, Xiao YB, Kumam, P (2020) Modified extragradient method for pseudomonotone variational inequalities in infinite dimensional Hilbert spaces. Vietnam J Math: 1–19
Yambangwai D, Aunruean S, Thianwan T (2019). A new modified three-step iteration method for G-nonexpansive mappings in Banach spaces with a graph. Numer Algorithms: 1–29
Acknowledgements
S. Suantai would like to thank Chiang Mai University, K. Kankam would like to thank Thailand Science Research and Innovation under the project IRN62W0007 and W. Cholamjiak would like to thank the revenue budget in 2021, School of Science, University of Phayao.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Carlos Hoppen.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Suantai, S., Kankam, K., Cholamjiak, P. et al. A parallel monotone hybrid algorithm for a finite family of \(G-\)nonexpansive mappings in Hilbert spaces endowed with a graph applicable in signal recovery. Comp. Appl. Math. 40, 145 (2021). https://doi.org/10.1007/s40314-021-01530-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40314-021-01530-6