Abstract
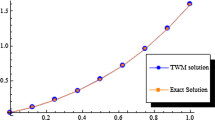
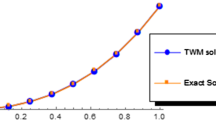
The main objective of this paper is to establish a fractional-order operational matrix method based on Euler wavelets for solving linear Volterra–Fredholm integro-differential equations with weakly singular kernel. First, the one-dimensional Euler wavelet is introduced, and then by using it, the operational matrix of fractional integration is constructed. Using the operational matrix of integration of fractional order, the weakly singular linear fractional Volterra–Fredholm integro-differential equations are reduced to a system of algebraic equations. The convergence of the proposed method has been analyzed and the numerical convergence rate for the presented scheme is established. Also, the error analysis of the proposed technique has been investigated. Furthermore, some numerical examples are solved to illustrate the applicability and efficiency of the proposed approach. Finally, a comparison of absolute error values obtained by different wavelet methods has been presented to clarify the error analysis of the proposed method.








































Similar content being viewed by others
References
Avazzadeh Z, Heydari MH, Cattani C (2019) Legendre wavelets for fractional partial integro-differential viscoelastic equations with weakly singular kernels. Eur Phys J plus 134(7):368
Bagley RL, Torvik PJ (1985) Fractional calculus in the transient analysis of viscoelastically damped structures. AIAA J 23(6):918–925
Baleanu D, Jajarmi A, Asad JH, Blaszczyk T (2017) The motion of a bead sliding on a wire in fractional sense. Acta Phys Pol, A 131:1561–1564
Baleanu D, Jajarmi A, Hajipour M (2018) On the nonlinear dynamical systems within the generalized fractional derivatives with Mittag–Leffler kernel. Nonlinear Dyn 94(1):397–414
Behera S, Saha Ray S (2020) An operational matrix based scheme for numerical solutions of nonlinear weakly singular partial integro-differential equations. Appl Math Comput 367:124771
He Y (2015) Some new results on products of Apostol-Bernoulli and Apostol-Euler polynomials. J Math Anal Appl 431(1):34–46
Hilfer R (2000) Applications of fractional calculus in physics. World Scientific
Ichise M, Nagayanagi Y, Kojima T (1971) An analog simulation of non-integer order transfer functions for analysis of electrode processes. J Electroanal Chem Interfacial Electrochem 33(2):253–265
Jajarmi A, Hajipour M, Mohammadzadeh E, Baleanu D (2018) A new approach for the nonlinear fractional optimal control problems with external persistent disturbances. J Franklin Inst 355(9):3938–3967
Jiang W, Tian T (2015) Numerical solution of nonlinear Volterra integro-differential equations of fractional order by the reproducing kernel method. Appl Math Model 39(16):4871–4876
Keshavarz E, Ordokhani Y (2019) A fast numerical algorithm based on the Taylor wavelets for solving the fractional integro-differential equations with weakly singular kernels. Math Methods Appl Sci 42(13):4427–4443
Kilbas AA, Srivastava HM, Trujillo JJ (2006) Theory and applications of fractional differential equations. Elsevier
Koeller RC (1984) Applications of fractional calculus to the theory of viscoelasticity. J Appl Mech 51:299–307
Mokhtary P (2016) Discrete Galerkin method for fractional integro-differential equations. Acta Math Sci 36(2):560–578
Nawaz Y (2011) Variational iteration method and homotopy perturbation method for fourth-order fractional integro-differential equations. Comput Math Appl 61(8):2330–2341
Nemati S, Lima PM (2018) Numerical solution of nonlinear fractional integro-differential equations with weakly singular kernels via a modification of hat functions. Appl Math Comput 327:79–92
Pedas A, Tamme E, Vikerpuur M (2016) Spline collocation for fractional weakly singular integro-differential equations. Appl Numer Math 110:204–214
Podlubny I (1998) Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Elsevier
Saeedi H, Moghadam MM (2011) Numerical solution of nonlinear Volterra integro-differential equations of arbitrary order by CAS wavelets. Commun Nonlinear Sci Numer Simul 16(3):1216–1226
Saha RS, Behera S (2019) A novel technique based on Bernoulli wavelets for numerical solutions of two-dimensional Fredholm integral equation of second kind. Eng Comput 36(6):1798–1819
Saha RS, Bera RK (2005) An approximate solution of a nonlinear fractional differential equation by Adomian decomposition method. Appl Math Comput 167(1):561–571
Sahu PK, Saha RS (2016) A numerical approach for solving nonlinear fractional Volterra-Fredholm integro-differential equations with mixed boundary conditions. Int J Wavelets Multiresolut Inf Process 14(05):1650036
Song L, Wang W (2013) A new improved Adomian decomposition method and its application to fractional differential equations. Appl Math Model 37(3):1590–1598
Srivastava HM, Pinter A (2004) Remarks on some relationships between the Bernoulli and Euler polynomials. Appl Math Lett 17(4):375–380
Wang Y, Zhu L (2016) SCW method for solving the fractional integro-differential equations with a weakly singular kernel. Appl Math Comput 275:72–80
Wang Y, Zhu L (2017) Solving nonlinear Volterra integro-differential equations of fractional order by using Euler wavelet method. Adv Difference Equ 1:1–16
Wang Y, Zhu L, Wang Z (2018) Fractional-order Euler functions for solving fractional integro-differential equations with weakly singular kernel. Adv Difference Equ 254(1):1–13
Yi M, Huang J (2015) CAS wavelet method for solving the fractional integro-differential equation with a weakly singular kernel. Int J Comput Math 92(8):1715–1728
Zhang X, Tang B, He Y (2011) Homotopy analysis method for higher-order fractional integro-differential equations. Comput Math Appl 62(8):3194–3203
Zhao J, Xiao J, Ford NJ (2014) Collocation methods for fractional integro-differential equations with weakly singular kernels. Numer Algorithms 65(4):723–743
Acknowledgements
The first author acknowledges the financial support under the scheme "Innovation in Science Pursuit for Inspired Research (INSPIRE)" fellowship vide Grant No. IF170719.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Vasily E. Tarasov.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Behera, S., Saha Ray, S. Euler wavelets method for solving fractional-order linear Volterra–Fredholm integro-differential equations with weakly singular kernels. Comp. Appl. Math. 40, 192 (2021). https://doi.org/10.1007/s40314-021-01565-9
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40314-021-01565-9
Keywords
- Fractional Volterra–Fredholm integro-differential equation
- Weakly singular kernels
- Euler wavelets
- Operational matrix