Skip to main content
SpringerLink
Log in

A wavelet-based novel technique for linear and nonlinear fractional Volterra–Fredholm integro-differential equations

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

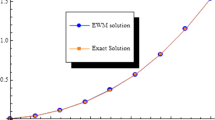
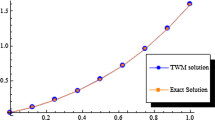
Abstract

In this paper, a wavelet-based operational matrix scheme has been introduced to obtain the approximate solution of the linear and nonlinear fractional order Volterra–Fredholm integro-differential equations. For the suggested approach, the operational matrix of the fractional integral for Taylor wavelets has been constructed. Then, the fractional integral operational matrix is utilized to reduce the solutions of linear and nonlinear Volterra–Fredholm integro-differential equations to systems of linear and nonlinear algebraic equations, respectively. Moreover, the convergence and error estimation of the proposed technique has been analyzed in this article. The numerical convergence rate is calculated to describe the accuracy of the presented method. Several illustrative experiments are included to verify the efficiency and validity of the proposed method. Also, the numerical results obtained by the suggested wavelet scheme have been compared with the other existing methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29
Fig. 30

Similar content being viewed by others

References

  • Akrami MH, Atabakzadeh MH, Erjaee GH (2013) The operational matrix of fractional integration for shifted Legendre polynomials. Iranian J Sci Tech 37(4):439–444

    MathSciNet  Google Scholar 

  • Ali MR, Hadhoud AR, Srivastava H (2019) Solution of fractional Volterra–Fredholm integro-differential equations under mixed boundary conditions by using the HOBW method. Adv Differ Equ 2019(1):1–14

    Article  MathSciNet  MATH  Google Scholar 

  • Alkan S, Hatipoglu VF (2017) Approximate solutions of Volterra–Fredholm integro-differential equations of fractional order. Tbilisi Math J 10(2):1–13

    Article  MathSciNet  MATH  Google Scholar 

  • Aziz I, Fayyaz M (2013) A new approach for numerical solution of integro-differential equations via Haar wavelets. Int J Comput Math 90(9):1971–1989

    Article  MathSciNet  MATH  Google Scholar 

  • Baleanu D, Jajarmi A, Hajipour M (2018) On the nonlinear dynamical systems within the generalized fractional derivatives with Mittag–Leffler kernel. Nonlinear Dyn 94(1):397–414

    Article  MATH  Google Scholar 

  • Behera S, Saha Ray S (2020) “An operational matrix based scheme for numerical solutions of nonlinear weakly singular partial integro-differential equations. Appl Math Comput 367:124771

    MathSciNet  MATH  Google Scholar 

  • Bhrawy AH, Alofi AS (2013) The operational matrix of fractional integration for shifted Chebyshev polynomials. Appl Math Lett 26(1):25–31

    Article  MathSciNet  MATH  Google Scholar 

  • Bhrawy AH, Tharwat MM, Alghamdi MA (2014) A new operational matrix of fractional integration for shifted Jacobi polynomials. Bull Malays Math Sci Soc 37(4):983–995

    MathSciNet  MATH  Google Scholar 

  • Das P, Rana S, Ramos H (2020) A perturbation-based approach for solving fractional-order Volterra–Fredholm integro differential equations and its convergence analysis. Int J Comput Math 97(10):1994–2014

    Article  MathSciNet  MATH  Google Scholar 

  • Hamoud AA, Ghadle KP (2018) Modified Laplace decomposition method for fractional Volterra–Fredholm integro-differential equations. J Math Model 6(1):91–104

    MathSciNet  MATH  Google Scholar 

  • Hamoud AA, Ghadle KP (2019) Some new existence, uniqueness and convergence results for fractional Volterra–Fredholm integro-differential equations. J Appl Comput Mech 5(1):58–69

    Google Scholar 

  • He JH (1999) Some applications of nonlinear fractional differential equations and their approximations. Bull Sci Technol 15(2):86–90

    Google Scholar 

  • Keshavarz E, Ordokhani Y (2019) A fast numerical algorithm based on the Taylor wavelets for solving the fractional integro-differential equations with weakly singular kernels. Math Methods Appl Sci 42(13):4427–4443

    Article  MathSciNet  MATH  Google Scholar 

  • Khajehnasiri AA (2016) Numerical solution of nonlinear 2D Volterra-Fredholm integro-differential equations by two-dimensional triangular function. Int J Appl Comput Math 2(4):575–591

    Article  MathSciNet  MATH  Google Scholar 

  • Liu N, Lin EB (2010) Legendre wavelet method for numerical solutions of partial differential equations. Numer Methods Part Diff Eq Int J 26(1):81–94

    Article  MathSciNet  MATH  Google Scholar 

  • Loh JR, Phang C, Isah A (2017) New operational matrix via Genocchi polynomials for solving Fredholm–Volterra fractional integro-differential equations. Adv Math Phys 2017:1–13

    Article  MathSciNet  MATH  Google Scholar 

  • Mainardi F (1997) Fractional calculus: some basic problems in continuum and statistical mechanics. Springer, New York

    MATH  Google Scholar 

  • Majeed A, Kamran M, Rafique M (2020) An approximation to the solution of time fractional modified Burgers’ equation using extended cubic B-spline method. Comput Appl Math 39(4):1–21

    Article  MathSciNet  MATH  Google Scholar 

  • Meng Z, Wang L, Li H, Zhang W (2015) Legendre wavelets method for solving fractional integro-differential equations. Int J Comput Math 92(6):1275–1291

    Article  MathSciNet  MATH  Google Scholar 

  • Milici C, Draganescu G, Tenreiro Machado JA (2019) Introduction to fractional differential equations. Springer International Publishing, Cham

    Book  MATH  Google Scholar 

  • Oldham K, Spanier J (1974) The fractional calculus theory and applications of differentiation and integration to arbitrary order. Elsevier, Amsterdam

    MATH  Google Scholar 

  • Pedas A, Tamme E (2006) Spline collocation method for integro-differential equations with weakly singular kernels. J Comput Appl Math 197(1):253–269

    Article  MathSciNet  MATH  Google Scholar 

  • Podlubny I (1998) Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Elsevier, Amsterdam

    MATH  Google Scholar 

  • Povstenko Y (2010) Signaling problem for time-fractional diffusion-wave equation in a halfspace in the case of angular symmetry. Nonlinear Dyn 59(4):593–605

    Article  MATH  Google Scholar 

  • Rabiei K, Ordokhani Y, Babolian E (2018) Numerical solution of 1D and 2D fractional optimal control of system via Bernoulli polynomials. Int J Appl Comput Math 4(1):1–17

    Article  MathSciNet  MATH  Google Scholar 

  • Saeedi H, Moghadam MM, Mollahasani N, Chuev GN (2011) A CAS wavelet method for solving nonlinear Fredholm integro-differential equations of fractional order. Commun Nonlinear Sci Numer Simul 16(3):1154–1163

    Article  MathSciNet  MATH  Google Scholar 

  • Saghali S, Javidi M, Saei FD (2019) Analytical solution of a fractional differential equation in the theory of viscoelastic fluids. Int J Appl Comput Math 5(3):1–13

    Article  MathSciNet  MATH  Google Scholar 

  • Saha RS (2008) A new approach for the application of Adomian decomposition method for the solution of fractional space diffusion equation with insulated ends. Appl Math Comput 202(2):544–549

    MathSciNet  MATH  Google Scholar 

  • Saha Ray S (2020) Nonlinear differential equations in physics. Springer Nature, Singapore

    Book  MATH  Google Scholar 

  • Sahu PK, Saha RS (2016a) A numerical approach for solving nonlinear fractional Volterra–Fredholm integro-differential equations with mixed boundary conditions. Int J Wavelets Multiresolut Inf Process 14(05):1650036

    Article  MathSciNet  MATH  Google Scholar 

  • Sahu PK, Saha RS (2016b) Sinc-Galerkin technique for the numerical solution of fractional Volterra–Fredholm integro-differential equations with weakly singular kernels. Int J Nonlinear Sci Numer Simul 17(6):315–323

    Article  MathSciNet  MATH  Google Scholar 

  • Stewart GW (1993) Afternotes on numerical analysis, University of Maryland at College Park

  • Tarasov VE (2009) Fractional integro-differential equations for electromagnetic waves in dielectric media. Theor Math Phys 158(3):355–359

    Article  MATH  Google Scholar 

  • Toan PT, Vo TN, Razzaghi M (2019) Taylor wavelet method for fractional delay differential equations. Eng Comput 37:1–10

    Google Scholar 

  • Vanani SK, Aminataei A (2011) Operational Tau approximation for a general class of fractional integro-differential equations. Comput Appl Math 30(3):655–674

    Article  MathSciNet  MATH  Google Scholar 

  • Wang Y, Zhu L (2017) 2017, Solving nonlinear Volterra integro-differential equations of fractional order by using Euler wavelet method. Adv Differ Equ 1:1–16

    Google Scholar 

  • Zhou F, Xu X (2019) Numerical solution of fractional Volterra–Fredholm integro-differential equations with mixed boundary conditions via Chebyshev wavelet method. Int J Comput Math 96(2):436–456

    Article  MathSciNet  MATH  Google Scholar 

  • Zhu L, Fan Q (2012) Solving fractional nonlinear Fredholm integro-differential equations by the second kind Chebyshev wavelet. Commun Nonlinear Sci Numer Simul 17(6):2333–2341

    Article  MathSciNet  MATH  Google Scholar 

  • Zhu L, Fan Q (2013) Numerical solution of nonlinear fractional-order Volterra integro-differential equations by SCW. Commun Nonlinear Sci Numer Simul 18(5):1203–1213

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The first author gratefully appreciates financial assistance from the fellowship scheme “Innovation in Science Pursuit of Inspired Research (INSPIRE)” under Grant No. IF170719.

Author information

Authors and Affiliations

  1. Department of Mathematics, National Institute of Technology Rourkela, Odisha, 769008, India

    S. Behera & S. Saha Ray

Authors
  1. S. Behera
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. Saha Ray
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Saha Ray.

Additional information

Communicated by Vasily E. Tarasov.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Behera, S., Ray, S.S. A wavelet-based novel technique for linear and nonlinear fractional Volterra–Fredholm integro-differential equations. Comp. Appl. Math. 41, 77 (2022). https://doi.org/10.1007/s40314-022-01772-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-022-01772-y

Keywords

Mathematics Subject Classification

Search

Navigation