Skip to main content

Advertisement

Springer Nature Link
Log in

Earth Mover’s divergence of belief function

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

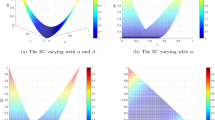
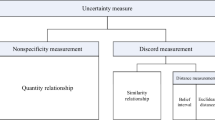
Abstract

Divergence is used to measure the difference of two systems, and it is widely applied in many fields. To solve this problem more efficiently, Dempster–Shafer evidence theory has been proposed, different from the traditional probability distribution, and because of its processing advantages of uncertainty, has been widely used in many aspects of reality. In this paper, a new method of belief divergence measure of mass functions is proposed, named as Earth Mover’s divergence of belief function, which is a generalization of Earth Mover’s distance (Wasserstein distance). Compared with other existing methods of divergence measuring, the EM divergence can show good performance in the presence of higher degrees of uncertainty and more conflicts. Numerical examples help have a better understanding of the Earth Mover’s divergence of belief function. Based on the new method of belief divergence measure, there is a combination model proposed to address the problem of data fusion. Application in target recognition is used to show the efficiency of the proposed method of divergence measure.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  • Arjovsky M, Chintala S, Bottou L (2017) Wasserstein generative adversarial networks. Int Conf Mach Learn. PMLR,214–223

  • Cao Z, Chuang C-H, King J-K, Lin C-T (2019) Multi-channel EEG recordings during a sustained-attention driving task. Sci Data. https://doi.org/10.1038/s41597-019-0027-4

  • Chang L, Zhang L, Fu C, Chen Y-W (2021) Transparent digital twin for output control using belief rule base. IEEE Trans Cybern. https://doi.org/10.1109/TCYB.2021.3063285,

  • Cheng C, Xiao F (2021) A distance for belief functions of orderable set. Pattern Recogn Lett 145:165–170

    Article  Google Scholar 

  • Cui H, Zhou L, Li Y, Kang B (2022) Belief entropy-of-entropy and its application in the cardiac interbeat interval time series analysis. Chaos Solitons Fractals 155:111736

    Article  MathSciNet  Google Scholar 

  • Dempster AP (1967) Upper and lower probabilities induced by a multivalued mapping. Ann Math Stat 382:325–339 (04)

    Article  MathSciNet  MATH  Google Scholar 

  • Deng Y (2020) Information volume of mass function. Int J Comput Commun Control 15(6):3983

    Article  Google Scholar 

  • Deng Y (2020) Uncertainty measure in evidence theory. SCIENCE CHINA Inf Sci 63(11):210201

    Article  MathSciNet  Google Scholar 

  • Deng Y (2022) Random permutation set. Int J Comput Commun Control 17(1):4542

    Article  Google Scholar 

  • Deng J, Deng Y (2021) Information volume of fuzzy membership function. Int J Comput Commun Control 16(1):4106

    Article  Google Scholar 

  • Deng X, Jiang W (2020) On the negation of a Dempster-Shafer belief structure based on maximum uncertainty allocation. Inf Sci 516:346–352

    Article  MathSciNet  MATH  Google Scholar 

  • Fan L, Deng Y (2021) Determine the number of unknown targets in Open World based on Elbow method. IEEE Trans Fuzzy Syst 29(5):986–995

    Article  Google Scholar 

  • Fei L, Feng Y, Liu L (2019) Evidence combination using OWA-based soft likelihood functions. Int J Intell Syst 34(9):2269–2290

    Article  Google Scholar 

  • Fei L, Lu J, Feng Y (2020) An extended best-worst multi-criteria decision-making method by belief functions and its applications in hospital service evaluation. Comput Ind Eng 142:106355

    Article  Google Scholar 

  • Feng F, Cho J, Pedrycz W, Fujita H, Herawan T (2016) Soft set based association rule mining. Knowl-Based Syst 111:268–282

    Article  Google Scholar 

  • Feng F, Xu Z, Fujita H, Liang M (2020) Enhancing PROMETHEE method with intuitionistic fuzzy soft sets. Int J Intell Syst 35:1071–1104

    Article  Google Scholar 

  • Fu C, Xue M, Chang W, Xu D, Yang S (2020) An evidential reasoning approach based on risk attitude and criterion reliability. Knowl-Based Syst 199:105947

    Article  Google Scholar 

  • Fujita H, Ko Y-C (2020) A heuristic representation learning based on evidential memberships: Case study of UCI-SPECTF. Int J Approx Reason 120

  • Gao X, Deng Y (2020) The pseudo-pascal triangle of maximum Deng entropy. Int J Comput Commun Control 15(1):1006

    Article  MathSciNet  Google Scholar 

  • Gao X, Pan L, Deng Y (2021) A generalized divergence of information volume and its applications. Eng Appl Artif Intell 108:104584

    Article  Google Scholar 

  • Gao Q, Wen T, Deng Y (2021) Information volume fractal dimension. Fractals 29(8):2150263

    Article  MATH  Google Scholar 

  • Garg H (2021) A new possibility degree measure for interval-valued q-rung orthopair fuzzy sets in decision-making. Int J Intell Syst 36(1):526–557

    Article  Google Scholar 

  • Garg H, Chen S (2020) Multiattribute group decision making based on neutrality aggregation operators of q-rung orthopair fuzzy sets. Inf Sci 517:427–447

    Article  MathSciNet  MATH  Google Scholar 

  • Han D, Dezert J, Yang Y (2016) Belief interval-based distance measures in the theory of belief functions. IEEE Trans Syst Man Cybern Syst 48(6):833–850

    Article  Google Scholar 

  • Herrmann V (2017) Wasserstein gan and the kantorovich-rubinstein duality. URL: https://vincentherrmann. github. io/blog/wasserstein

  • Jiang W, Cao Y, Deng X (2020) A novel Z-network model based on Bayesian network and Z-number. IEEE Trans Fuzzy Syst 28(8):1585–1599

    Article  Google Scholar 

  • Jousselme A-L, Grenier D, Bossé É (2001) A new distance between two bodies of evidence. Inf fusion 2(2):91–101

    Article  Google Scholar 

  • Kullback S (1997) Information theory and statistics. Courier Corporation

  • Lai JW, Chang J, Ang L, Cheong KH (2020) Multi-level information fusion to alleviate network congestion. Inf Fusion 63:248–255

    Article  Google Scholar 

  • Li Y, Deng Y (2018) Generalized ordered propositions fusion based on belief entropy. Int J Comput Commun Control 13(5):792–807

    Article  Google Scholar 

  • Liao H, Ren Z, Fang R (2020) A Deng-entropy-based evidential reasoning approach for multi-expert multi-criterion decision-making with uncertainty. Int J Comput Commun Control 13(1):1281–1294

    Google Scholar 

  • Liu Z-G, Huang L-Q, Zhou K, Denoeux T(2020) Combination of transferable classification with multisource domain adaptation based on evidential reasoning. IEEE Trans Neural Netw Learn Syst. https://doi.org/10.1109/TNNLS.2020.2995862,

  • Liu P, Gao H (2019) Some intuitionistic fuzzy power bonferroni mean operators in the framework of Dempster-Shafer theory and their application to multicriteria decision making. Appl Soft Comput 85:105790

    Article  Google Scholar 

  • Liu Z, Liu Y, Dezert J, Cuzzolin F (2020) Evidence combination based on credal belief redistribution for pattern classification. IEEE Trans Fuzzy Syst 28(4):618–631

    Article  Google Scholar 

  • Meng D, Li Y, He C, Guo J, Lv Z, Wu P (2021) Multidisciplinary design for structural integrity using a collaborative optimization method based on adaptive surrogate modelling. Mater Des 206:109789

    Article  Google Scholar 

  • Meng D, Hu Z, Wu P, Zhu S-P, Correia JA, De Jesus AM (2020) “Reliability-based optimisation for offshore structures using saddlepoint approximation. In: Proceedings of the Institution of Civil Engineers-Maritime Engineering, vol. 173, no. 2.Thomas Telford Ltd, 33–42

  • Meng D, Xie T, Wu P, He C, Hu Z, Lv Z (2021) An uncertainty-based design optimization strategy with random and interval variables for multidisciplinary engineering systems. In: Structures, vol. 32.Elsevier, pp 997–1004

  • Mo H (2021) A SWOT method to evaluate safety risks in life cycle of wind turbine extended by D number theory. J Intell Fuzzy Syst 40(3):4439–4452

    Article  Google Scholar 

  • Ni L, Chen Y-W, de Brujin O (2021) Towards understanding socially influenced vaccination decision making: an integrated model of multiple criteria belief modelling and social network analysis. Eur J Oper Res 293(1):276–289

    Article  MathSciNet  MATH  Google Scholar 

  • Shafer G (1976) A mathematical theory of evidence. Princeton university press Princeton,1

  • Song Y, Deng Y (2019) Divergence measure of belief function and its application in data fusion. IEEE Access 7:107465–107472

    Article  Google Scholar 

  • Song X, Xiao F (2022) Combining time-series evidence: A complex network model based on a visibility graph and belief entropy. Appl Intell. https://doi.org/10.1007/s10489-021-02956-5

  • Tang M, Liao H, Mi X, Xu X, Herrera F (2020) Dynamic subgroup-quality-based consensus in managing consistency, nearness, and evenness quality indices for large-scale group decision making under hesitant environment. J Oper Res Soc 1–14

  • Tian Y, Liu L, Mi X, Kang B (2020) ZSLF: A new soft likelihood function based on Z-numbers and its application in expert decision system,. IEEE Trans Fuzzy Syst. https://doi.org/10.1109/TFUZZ.2020.2997328,

  • Wang H, Fang Y-P, Zio E (2021) Risk assessment of an electrical power system considering the influence of traffic congestion on a hypothetical scenario of electrified transportation system in new york state. IEEE Trans Intell Transp Syst 22(1):142–155

    Article  Google Scholar 

  • Wen T, Cheong KH (2021) The fractal dimension of complex networks: a review. Inf Fusion 73:87–102

    Article  Google Scholar 

  • Xiao F (2022) CEQD: A complex mass function to predict interference effects. IEEE Trans Cybern 52(8): 7402–7414

  • Xiao F (2021) On the maximum entropy negation of a complex-valued distribution. IEEE Trans Fuzzy Syst 29(11): 3259–3269

  • Xiao F (2022) CaFtR: A fuzzy complex event processing method. Int J Fuzzy Syst 24(2): 1098–1111

  • Xiao F (2019) Multi-sensor data fusion based on the belief divergence measure of evidences and the belief entropy. Inf Fusion 46:23–32

    Article  Google Scholar 

  • Xiao F (2020) Evidence combination based on prospect theory for multi-sensor data fusion. ISA Trans 106:253–261

    Article  Google Scholar 

  • Xie D, Xiao F, Pedrycz W (2022) Information quality for intuitionistic fuzzy values with its application in decision making. Eng Appl Artif Intell. https://doi.org/10.1016/j.engappai.2021.104568,

  • Xu X, Zheng J, Yang J-B, Xu D-L, Chen Y-W (2017) Data classification using evidence reasoning rule. Knowl-Based Syst 116:144–151

    Article  Google Scholar 

  • Yager RR (2018) Interval valued entropies for Dempster-Shafer structures. Knowl-Based Syst 161:390–397

    Article  Google Scholar 

  • Yager RR, Elmore P, Petry F (2017) Soft likelihood functions in combining evidence. Inf Fusion 36:185–190

    Article  Google Scholar 

  • Ye J, Zhan J, Ding W, Fujita H (2021) A novel fuzzy rough set model with fuzzy neighborhood operators. Inf Sci 544:266–297

    Article  MathSciNet  MATH  Google Scholar 

  • Yong D, Wenkang S, Zhenfu Z, Qi L (2004) Combining belief functions based on distance of evidence. Decis Support Syst 38(3):489–493

    Article  Google Scholar 

  • Zhang S, Han D, Yang Y (2020) Active learning based on belief functions. SCIENCE CHINA Inf Sci 63(11):210205

    Article  MathSciNet  Google Scholar 

  • Zhou J, Su X, Qian H (2020) Risk assessment on offshore photovoltaic power generation projects in china using D umbers and anp. IEEE Access 99:1–1

    Google Scholar 

  • Zhou Z, Feng Z, Hu C, Hu G, He W, Han X (2020) Aeronautical relay health state assessment model based on belief rule base with attribute reliability. Knowl-Based Syst 197:105869

    Article  Google Scholar 

  • Zhou M, Liu X-B, Chen Y-W, Qian X-F, Yang J-B, Wu J (2020) Assignment of attribute weights with belief distributions for MADM under uncertainties. Knowl-Based Syst 189:105110

    Article  Google Scholar 

Download references

Acknowledgements

This research is supported by the National Natural Science Foundation of China (No. 62003280), Chongqing Talents: Exceptional Young Talents Project (No. cstc2022ycjh-bgzxm0070), and Chongqing Overseas Scholars Innovation Program (No. cx2022024). The authors greatly appreciate the reviewers’ suggestions and editor’s encouragement.

Author information

Authors and Affiliations

  1. School of Computer Science and Software, Southwest University of China, Chongqing, 400715, China

    Peilin Liu

  2. School of Big Data and Software Engineering, Chongqing University, Chongqing, 401331, China

    Peilin Liu & Fuyuan Xiao

  3. National Engineering Laboratory for Integrated Aero-Space-Ground-Ocean Big Data Application Technology, Xi’an, China

    Fuyuan Xiao

Authors
  1. Peilin Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Fuyuan Xiao
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Fuyuan Xiao.

Additional information

Communicated by Graçaliz Pereira Dimuro.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, P., Xiao, F. Earth Mover’s divergence of belief function. Comp. Appl. Math. 41, 292 (2022). https://doi.org/10.1007/s40314-022-02000-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-022-02000-3

Keywords

Mathematics Subject Classification