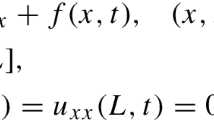Abstract
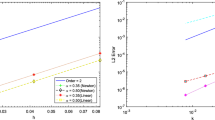
A second-order difference method on graded meshes is proposed for the multi-term fourth-order evolution equation (FOEE). We handle the Riemann–Liouvile fractional integral by the product integration rule on the graded meshes and the spatial derivatives by the second order central difference formula. Stability and convergence of the \(L^2\)-norm is provided. Finally, some numerical examples are given to verify the theoretical analysis and the validity of the proposed method.


Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.References
Atkinson EK (1997) The numerical solution of integral equations of the second kind. Cambridge Univerisity Press, New York
Baratella P (1997) A note on the convergence of product integration and Galerkin method for weakly singular integral equations. J Comput Appl Math 85:11–18
Chen H, Xu D (2006) A second-order fully discrete difference scheme for a partial integro-differential equation (in Chinese). Math Numer Sin 28:141–154
Chen H, Xu D, Zhou J (2019) A second-order accurate numerical method with graded meshes for an evolution equation with a weakly singular kernel. J Comput Appl Math 356:152–163
Chen H, Xu D, Cao JL, Zhou J (2020) A formally second order BDF ADI difference scheme for the three-dimensional time-fractional heat equation. Int J Comput Math 97:1100–1117
Das S (2011) Observation of fractional calculus in physical description: functional fractional calculus. Springer, Berlin, pp 101–156
Garrappa R (2015) Trapezoidal methods for fractional differential equations: theoretical and computational aspects. Math Comput Simul 110:96–112
Hu X, Zhang L (2011) A compact finite difference scheme for the fourth-order fractional diffusion-wave system. Comput Phys Commun 182:1645–1650
Hu X, Zhang L (2012) On finite difference methods for fourth-order fractional diffusion-wave and sub-diffusion systems. Appl Math Comput 218:5019–5034
Hu SF, Qiu WL, Chen H (2019) A backward Euler difference scheme for the integro-differential equations with the multi-term kernels. Int J Comput Math 97:1254–1267
Lopez-Marcos JC (1990) A difference scheme for a nonlinear partial integro-differential equation. SIAM J Numer Anal 27:20–31
Magin RL (2006) Fractional calculus in bioengineering. Begell House, Redding
Mainardi F, Raberto M, Gorenflo R, Scalas E (2000) Fractional calculus and contionous-time finance. II: the waiting-time distribution. Physica A 287:468–481
Mclean W, Thomee V, Wahlbin LB (1996) Discretization with variable time steps of an evolution equation with a positive-type memory term. J Comput Appl Math 69:49–69
Mustapha K (2010) A second-order accurate numerical method for a semilinear integro-differential equation with a weakly singular kernel. IMA J Numer Anal 30:555–578
Qiu WL, Xu D, Chen HB (2020) A formally second-order BDF finite difference scheme for the integro-differential equations with the multi-term kernels. Int J Comput Math 97:2055–2073
Scalas E, Gorenflo R, Mainardi F (2000) Fractional calclus and continuous-time finance. Physica A 284:376–384
Tao T (1993) A finite difference scheme for partial integro-differential equations with a weakly singular kernel. Appl Numer Math 11:309–319
Xu D, Qiu W, Guo J (2020) A compact finite difference scheme for the fourth-order time-fractional integro-differential equation with a weakly singular kernel. Numer Methods Partial Differ Equ 36:439–458
Yang XH, Zhang HX (2022) The uniform \(l^1\) long-time behavior of time discretization for time-fractional partial differential equations with nonsmooth data. Appl Math Lett 124:107644
Yang XH, Xu D, Zhang HX (2011) Quasi-wavelet based numerical method for fourth-order partial integro-differential equations with a weakly singular kernel. Int J Comput Math 88:3236–3254
Yang XH, Xu D, Zhang HX (2013) Crank–Nicolson/quasi-wavelets method for solving fourth order partial integro-differential equation with a weakly singular kernel. J Comput Phys 234:317–329
Yang XH, Zhang HX, Tang J (2021) The OSC solver for the fourth-order sub-diffusion equation with weakly singular solutions. Comput Math Appl 82:1–12
Zhang YN, Sun ZZ, Wu HW (2011) Error estimates of Crank–Nicolson type difference scheme for the sub-diffusion equation. SIAM J Numer Anal 49:2302–2322
Zhu L, Fan QB (2012) Solving fractional nonlinear Fredholm integro differential equations by the second kind Chebyshev wavelet. Commun Nonlinear Sci Numer Simul 17:2333–2341
Acknowledgements
We thank the anonymous referees for their valuable comments and suggestions which helped us to improve the manuscript a lot.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Hui Liang.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The work was supported by National Natural Science Foundation of China (12126321), Scientific Research Fund of Hunan Provincial Education Department (21B0550), Hunan Provincial Natural Science Foundation of China (2022JJ50083, 2021JJ30209), and Scientific research and innovation Foundation of Hunan University of Technology (CX2115, CX2114)
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Wu, L., Zhang, H., Yang, X. et al. A second-order finite difference method for the multi-term fourth-order integral–differential equations on graded meshes. Comp. Appl. Math. 41, 313 (2022). https://doi.org/10.1007/s40314-022-02026-7
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40314-022-02026-7