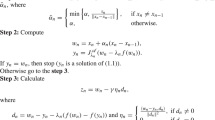Abstract
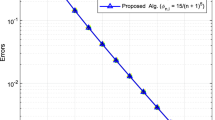
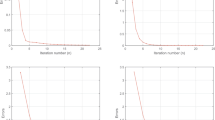
Several authors have studied and proposed different iterative methods for approximating a common solution of variational inequality problem and other optimization problems. In solving this common solution problem, authors often require that the variational inequality operator be co-coercive and very stringent conditions are often imposed on the control parameters for convergence. These restrictions may limit the usefulness of these existing methods in several applications. To remedy these drawbacks, we introduce a new projection and contraction method, which employs inertial technique and self-adaptive step size for approximating a common solution of split monotone variational inclusion problem (SMVIP), variational inequality problem (VIP) and common fixed point problem (CFPP) for an infinite family of strict pseudo-contractions. We establish strong convergence result for the proposed method when the variational inequality operator is pseudomonotone and Lipschitz continuous, but without the knowledge of the Lipschitz constant nor knowledge of the operator norm and without assuming the sequentially weakly continuity condition often assumed by authors. Finally, we apply our results to study other optimization problems and we present several numerical experiments with graphical illustrations to demonstrate the efficiency of our method in comparison with some of the existing methods. Our results in this study complement several existing ones in this direction in the current literature.


Similar content being viewed by others
References
Alakoya TO, Mewomo OT (2022) Viscosity S-iteration method with inertial technique and self-adaptive step size for split variational inclusion, equilibrium and fixed point problems. Comput Appl Math 41(1):31
Alakoya TO, Mewomo OT, Shehu Y (2022) Strong convergence results for quasimonotone variational inequalities. Math Methods Oper Res 47:30
Alakoya TO, Uzor VA, Mewomo OT, Yao J-C (2022) On a system of monotone variational inclusion problems with fixed-point constraint. J Inequ Appl 47:33
Alansari M, Farid M, Ali R (2020) An iterative scheme for split monotone variational inclusion, variational inequality and fixed point problems. Adv Differ Equ 485:21
Atsushiba S, Takahashi W (1999) Strong convergence theorems for a finite family of nonexpansive mappings and applications. Indian J Math 41:435–453
Bauschke HH, Borwein JM (1996) On projection algorithms for solving convex feasibility problems. SIAM Rev 38:367–426
Byrne C (2002) Iterative oblique projection onto convex sets and the split feasibility problem. Inverse Probl 18:441–453
Byrne C, Censor Y, Gibali A, Reich S (2012) The split common null point problem. Nonlinear Convex Anal 13:759–775
Censor Y, Borteld T, Martin B, Trofimov A (2006) A unified approach for inversion problems in intensity-modulated radiation therapy. Phys Med Biol 51:2353–2365
Censor Y, Elfving T (1994) A multiprojection algorithm using Bregman projections in a product space. Numer Algorith 8:221–239
Chang SS, Lee HWJ, Chan CK (2009) A new method for solving equilibrium problem fixed point problem and variational inequality problem with application to optimization. Nonlinear Anal 70:3307–3319
Chen P, Huang J, Zhang X (2013) A primal-dual fixed point algorithm for convex separable minimization with applications to image restoration. Inverse Probl 29(2):Art. ID 025011
Chen R, Yao Y (2010) Strong convergence theorems for strict pseudo-contractions in Hilbert spaces. J Appl Math Comput 32:69–82
Chuang CS (2013) Strong convergence theorems for the split variational inclusion problem in Hilbert spaces. Fixed Point Theory Appl 350:20
Combettes PL (1996) The convex feasibility problem in image recovery. Adv Imaging Electron Phys 95:155–270
Cubiotti P, Yao J-C (2022) Some qualitative properties of solutions of higher-order lower semicontinus differential inclusions. J Nonlinear Var Anal 6:585–599
Deepho J, Thounthong P, Kumam P, Phiangsungnoen S (2017) A new general iterative scheme for split variational inclusion and fixed point problems of k-strict pseudo-contraction mappings with convergence analysis. J Comput Appl Math 318:293–306
Dilshad M, Aljohani AF, Akram M (2020) Iterative scheme for split variational inclusion and a fixed-point problem of a finite collection of nonexpansive mappings. J Funct Spaces 2:10
Dong QL, Cho YJ, Rassias TM (2018) The projection and contraction methods for finding common solutions to variational inequality problems. Optim Lett 12:1871–189
Dong QL, Cho YJ, Zhong LL et al (2018) Inertial projection and contraction algorithms for variational inequalities. J Global Optim 70:687–704
Fichera G (1963) Sul problema elastostatico di Signorini con ambigue condizioni al contorno. Atti Accad Naz Lincei VIII Ser Rend Cl Sci Fis Mat Nat 34:138–142
Gibali A, Shehu Y (2019) An efficient iterative method for finding common fixed point and variational inequalities in Hilbert spaces. Optimization 68(1):13–32
Gibali A, Suleiman YI (2022) Parallel projection method for solving split equilibrium problems. J Appl Numer Optim 4:161–173
Godwin EC, Alakoya TO, Mewomo OT, Yao J-C (2022) Relaxed inertial Tseng extragradient method for variational inequality and fixed point problems. Appl Anal. https://doi.org/10.1080/00036811.2022.2107913
Godwin EC, Izuchukwu C, Mewomo OT (2022) Image restoration using a modified relaxed inertial method for generalized split feasibility problems Math. Methods Appl Sci. https://doi.org/10.1002/mma.8849
He BS (1997) A class of projection and contraction methods for monotone variational inequalities. Appl Math Optim 35:69–76
Iiduka H (2012) Fixed point optimization algorithm and its application to network bandwidth allocation. J Comput Appl Math 236(7):1733–1742
Jolaoso LO, Alakoya TO, Taiwo A, Mewomo OT (2021) Inertial extragradient method via viscosity approximation approach for solving Equilibrium problem in Hilbert space. Optimization 70(2):387–412
Jolaoso LO, Sunthrayuth P, Cholamjiak P, Cho YJ (2022) Analysis of two versions of relaxed inertial algorithms with Bregman divergences for solving variational inequalities. Comput Appl Math 41:300
Jolaoso LO, Taiwo A, Alakoya TO, Mewomo OT (2020) A Strong Convergence Theorem for Solving Pseudo-monotone Variational Inequalities Using Projection Methods. J Optim Theory Appl 185:744–766
Kazmi KR, Rizvi SH (2014) An iterative method for split variational inclusion problem and fixed point problem for a nonexpansive mapping. Optim Lett 8:1113–1124
Khan SH, Alakoya TO, Mewomo OT (2020) Relaxed projection methods with self-adaptive step size for solving variational inequality and fixed point problems for an infinite family of multivalued relatively nonexpansive mappings in Banach spaces. Math Comput Appl 25:54
Korpelevich GM (1976) An extragradient method for finding saddle points and other problems. Ekon Mat Metody 12:747–756
Liu H, Yang J (2020) Weak convergence of iterative methods for solving quasimonotone variational inequalities. Comput Optim Appl 77:491–508
López G, Martín-Márquez V, Xu HK (2010) Iterative algorithms for the multiple-sets split feasibility problem. Biomedical Mathematics: Promising Directions in Imaging, TherapyPlanning and Inverse Problems, Medical Physics Publishing, Madison, 243-279
Luo C, Ji H, Li Y (2009) Utility-based multi-service bandwidth allocation in the 4G heterogeneous wireless networks. IEEE Wireless Communication and Networking Conference, 1–5, https://doi.org/10.1109/WCNC.2009.4918017
Maingé PE (2008) A hybrid extragradient-viscosity method for monotone operators and fixed point problems. SIAM J Control Optim 47:1499–1515
Moudafi A (2011) Split monotone variational inclusions. J Opt Theory Appl 150:275–283
Ogwo GN, Alakoya TO, Mewomo OT (2021) Iterative algorithm with self-adaptive step size for approximating the common solution of variational inequality and fixed point problems. Optimization. https://doi.org/10.1080/02331934.2021.1981897
Ogwo GN, Alakoya TO, Mewomo OT (2022) Inertial Iterative method with self-adaptive step size for finite family of split monotone variational inclusion and fixed point problems in Banach spaces. Demonstr Math 55(1):193–216
Ogwo GN, Izuchukwu C, Mewomo OT (2022) Relaxed inertial methods for solving split variational inequality problems without product space formulation. Acta Math Sci Ser B (Engl Ed) 42(5):1701–1733
Onjai-uea N, Phuengrattana W (2017) On solving split mixed equilibrium problems and fixed point problems of hybrid-type multivalued mappings in Hilbert spaces. J Inequal Appl 2:137
Opial Z (1967) Weak convergence of the sequence of successive approximation for nonexpansive mappings. Bull Am Math Soc 73:591–597
Owolabi AO-E, Alakoya TO, Taiwo A, Mewomo OT (2022) A new inertial-projection algorithm for approximating common solution of variational inequality and fixed point problems of multivalued mappings. Numer Algebra Control Optim 12(2):257–278
Rockafellar RT (1970) On the maximality of sums of nonlinear monotone operators. Trans Am Math Soc 149:75–288
Saejung S, Yotkaew P (2012) Approximation of zeros of inverse strongly monotone operators in Banach spaces. Nonlinear Anal 75:742–750
Shahazad N, Zegeye H (2014) Approximating of common point of fixed points of a pseudo-contractive mapping and zeros of sum of monotone mappings. Fixed Point Theory Appl 85:15
Shehu Y (2016) Iterative approximations for zeros of sum of accretive operators in Banach spaces. J Funct Spaces 2:9
Shehu Y, Iyiola OS, Ogbuisi FU (2020) Iterative method with inertial terms for nonexpansive mappings: applications to compressed sensing. Numer Algorith 83:1321–1347
Shimoji K, Takahashi W (2001) Strong convergence to common fixed points of infinite nonexpansive mappings and applications Taiwanese. J Math 5:387–404
Stampacchia G (1968) Variational Inequalities. In: Theory and Applications of Monotone Operators, Proceedings of the NATO Advanced Study Institute, Venice, Italy (Edizioni Odersi, Gubbio, Italy, 1968), 102–192
Suantai S, Shehu Y, Cholamjiak P (2019) Nonlinear iterative methods for solving the split common null point problem in Banach spaces. Optim Methods Softw 34(4):853–874
Taiwo A, Alakoya TO, Mewomo OT (2021) Halpern-type iterative process for solving split common fixed point and monotone variational inclusion problem between Banach spaces. Numer Algorith 86(4):1359–1389
Takahashi W (2009) Introduction to nonlinear and convex analysis. Yokohama Publishers, Yokohama
Takahashi S, Takahashi W, Toyoda MT (2010) Strong convergence theorem for maximal monotone operators with nonlinear mappings in Hilbert spaces. J Optim Theory Appl 147:27–41
Thong DV, Hieu DV, Rassias TM (2020) Self adaptive inertial subgradient extragradient algorithms for solving pseudomonotone variational inequality problems. Optim Lett 14(1):115–144
Thong DV, Long LV, Li X-H, Dong Q-L, Cho YJ, Tuan PA (2021) A new self-adaptive algorithm for solving pseudomonotone variational inequality problems in Hilbert spaces. Optimization. https://doi.org/10.1080/02331934.2021.1909584
Uzor VA, Alakoya TO, Mewomo OT (2022) Strong convergence of a self-adaptive inertial Tseng’s extragradient method for pseudomonotone variational inequalities and fixed point problems. Open Math 20:234–257
Wang S (2011) A general iterative method for obtaining an infinite family of strictly pseudo-contractive mappings in Hilbert spaces. Appl Math Lett 24:901–907
Zhao J, Liang Y, Liu Y, Cho YJ (2018) Split equilibrium, variational inequality and fixed point problems for multi-valued mappings in Hilbert spaces. Appl Comput Math 17(3):271–283
Zhou Y (2008) Convergence theorems of fixed points for \(k\)-strict pseudo-contractions in Hilbert spaces. Nonlinear Anal 69:456–462
Acknowledgements
The authors sincerely thank the editor and anonymous referees for their careful reading, constructive comments, and useful suggestions that improved the manuscript. The research of the first author is wholly supported by the University of KwaZulu-Natal, Durban, South Africa Postdoctoral Fellowship. He is grateful for the funding and financial support. The second author acknowledges with thanks the International Mathematical Union Breakout Graduate Fellowship (IMU-BGF) Award for his doctoral study. The third author is supported by the National Research Foundation (NRF) of South Africa Incentive Funding for Rated Researchers (Grant Number 119903). Opinions expressed and conclusions arrived are those of the authors and are not necessarily to be attributed to the NRF.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no competing interests.
Additional information
Communicated by Baisheng Yan.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix 7.1.
Appendix 7.1.
(Algorithm 3.1 in [31])

where \(\gamma \in (0, \frac{1}{L}),\) where L is the spectral radius of the operator \(A^*A,\) and \(A^*\) is the adjoint of A and \(T: H_1\rightarrow H_1\) is a nonexpansive mapping and
-
(i)
\(\alpha _n\in (0,1),\lim _{n\rightarrow +\infty }\alpha _n=0, \sum _{n=1}^{\infty }\alpha _n=+\infty ;\) (ii) \(\sum _{n=1}^{\infty }|\alpha _n-\alpha _{n-1}|<+\infty .\)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Alakoya, T.O., Uzor, V.A. & Mewomo, O.T. A new projection and contraction method for solving split monotone variational inclusion, pseudomonotone variational inequality, and common fixed point problems. Comp. Appl. Math. 42, 3 (2023). https://doi.org/10.1007/s40314-022-02138-0
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40314-022-02138-0
Keywords
- Projection and contraction method
- Split monotone variational inclusion problem
- Variational inequality problem
- Strict pseudo-contractions
- Inertial technique
- Adaptive step size