Skip to main content
SpringerLink
Log in

Data-driven learning of differential equations: combining data and model uncertainty

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

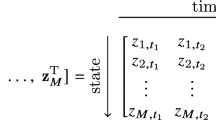
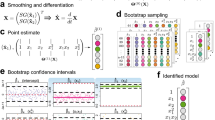
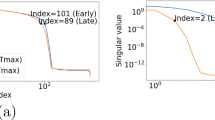
Abstract

Data-driven discovery of differential equations relies on estimating model parameters using information about a solution that is often incomplete and corrupted by noise. Moreover, the sizes of the uncertainties in the model and data are usually unknown as well. This paper develops a likelihood-type cost function which incorporates both sources of uncertainty and provides a theoretically justified way of optimizing the balance between them. This approach accommodates missing information about model solutions, allows for considerable noise in the data, and is demonstrated to provide estimates which are often superior to regression methods currently used for model discovery and calibration. Practical implementation and optimization strategies are discussed both for systems of ordinary differential and partial differential equations. Numerical experiments using synthetic data are performed for a variety of test problems, including those exhibiting chaotic or complex spatiotemporal behavior.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  • Ackleh Azmy S, Ferdinand Robert R, Simeon R (1998) Numerical studies of parameter estimation techniques for nonlinear evolution equations. Kybernetika 34(6):693–712

    MathSciNet  MATH  Google Scholar 

  • Ashyraliyev M, Jaeger J, Blom JG (2008) Parameter estimation and determinability analysis applied to drosophila gap gene circuits. BMC Syst Biol 2(1):83

    Article  Google Scholar 

  • Barajas-Solano David A, Tartakovsky Alexandre M (2019) Approximate Bayesian model inversion for pdes with heterogeneous and state-dependent coefficients. J Comput Phys 395:247–262

    Article  MathSciNet  MATH  Google Scholar 

  • Barry RP, Pace RK (1999) Monte Carlo estimates of the log determinant of large sparse matrices. Linear Algebra Appl 289(1–3):41–54

    Article  MathSciNet  MATH  Google Scholar 

  • Boutsidis C, Drineas P, Kambadur P, Kontopoulou E-M, Zouzias A (2017) A randomized algorithm for approximating the log determinant of a symmetric positive definite matrix. Linear Algebra Appl 533:95–117

    Article  MathSciNet  MATH  Google Scholar 

  • Brunel NJB (2008) Parameter estimation of ode’s via nonparametric estimators. Electron J Stat 2:1242–1267

    Article  MathSciNet  MATH  Google Scholar 

  • Brunton Steven L, Proctor Joshua L, Kutz J Nathan (2016) Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc Natl Acad Sci 113(15):3932–3937

  • Brynjarsdottir J, O’Hagan A (2014) Learning about physical parameters: the importance of model discrepancy. Inverse Probl 30(11):114007

  • Croft W, Elliott CM, Ladds Graham SB, Chandrasekhar V, Cathryn W (2015) Parameter identification problems in the modelling of cell motility. J Math Biol 71(2):399–436

    Article  MathSciNet  MATH  Google Scholar 

  • Cross MC, Hohenberg PC (1993) Pattern formation outside of equilibrium. Rev Mod Phys 65(3):851

    Article  MATH  Google Scholar 

  • Dewar MA, Kadirkamanathan V, Opper M, Sanguinetti G (2010) Parameter estimation and inference for stochastic reaction-diffusion systems: application to morphogenesis in D melanogaster. BMC Syst Biol 4(1):21

    Article  Google Scholar 

  • Evensen G (2009) Data assimilation: the ensemble Kalman filter. Springer, New York

    Book  MATH  Google Scholar 

  • Fullana JM, Le Gal P, Rossi M, Zaleski S (1997) Identification of parameters in amplitude equations describing coupled wakes. Phys D Nonlinear Phenom 102(1–2):37–56

    Article  MATH  Google Scholar 

  • Garvie MR, Maini PK, Trenchea C (2010) An efficient and robust numerical algorithm for estimating parameters in turing systems. J Comput Phys 229(19):7058–7071

    Article  MathSciNet  MATH  Google Scholar 

  • Glasner K (2021) Optimization algorithms for parameter identification in parabolic partial differential equations. Comput Appl Math 40(4):1–22

    Article  MathSciNet  MATH  Google Scholar 

  • Glasner K, Orizaga S (2016) Improving the accuracy of convexity splitting methods for gradient flow equations. J Comput Phys 315:52–64

    Article  MathSciNet  MATH  Google Scholar 

  • Gugushvili S, Klaassen CAJ (2012) \(\sqrt{n}\)-consistent parameter estimation for systems of ordinary differential equations: bypassing numerical integration via smoothing. Bernoulli 18(3):1061–1098

    Article  MathSciNet  MATH  Google Scholar 

  • Hager William W, Hongchao Z (2006) A survey of nonlinear conjugate gradient methods. Pac J Optim 2(1):35–58

    MathSciNet  MATH  Google Scholar 

  • Jin B, Maass P (2012) Sparsity regularization for parameter identification problems. Inverse Probl 28(12):123001

    Article  MathSciNet  MATH  Google Scholar 

  • Kennedy MC, O’Hagan A (2001) Bayesian calibration of computer models. J R Stat Soc Ser B Stat Methodol 63(3):425–464

    Article  MathSciNet  MATH  Google Scholar 

  • Kingma DP, Ba J (2014) Adam: a method for stochastic optimization. arXiv preprint arXiv:1412.6980

  • Liang H, Hulin W (2008) Parameter estimation for differential equation models using a framework of measurement error in regression models. J Am Stat Assoc 103(484):1570–1583

    Article  MathSciNet  MATH  Google Scholar 

  • Long Z, Lu Y, Dong B (2019) Pde-net 2.0: learning pdes from data with a numeric-symbolic hybrid deep network. J Comput Phys 399:108925

    Article  MathSciNet  MATH  Google Scholar 

  • Maddu S, Cheeseman BL, Sbalzarini IF, Müller CL (2019) Stability selection enables robust learning of partial differential equations from limited noisy data. arXiv preprint arXiv:1907.07810

  • Messenger Daniel A, Bortz David M (2021) Weak sindy for partial differential equations. J Comput Phys 443:110525

    Article  MathSciNet  MATH  Google Scholar 

  • Plumlee M (2017) Bayesian calibration of inexact computer models. J Am Stat Assoc 112(519):1274–1285

    Article  MathSciNet  Google Scholar 

  • Raissi M, Karniadakis GE (2018) Hidden physics models: machine learning of nonlinear partial differential equations. J Comput Phys 357:125–141

    Article  MathSciNet  MATH  Google Scholar 

  • Raissi M, Perdikaris P, Karniadakis GE (2017) Machine learning of linear differential equations using gaussian processes. J Comput Phys 348:683–693

    Article  MathSciNet  MATH  Google Scholar 

  • Raissi M, Perdikaris P, Karniadakis GE (2019) Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J Comput Phys 378:686-707

  • Ramsay J, Hooker G (2017) Dynamic data analysis. Springer, New York

    Book  MATH  Google Scholar 

  • Ramsay JO, Hooker G, Campbell D, Cao J (2007) Parameter estimation for differential equations: a generalized smoothing approach. J R Stat Soc Ser B Stat Methodol 69(5):741–796

    Article  MathSciNet  MATH  Google Scholar 

  • Reinbold Patrick AK, Gurevich Daniel R, Grigoriev Roman O (2020) Using noisy or incomplete data to discover models of spatiotemporal dynamics. Phys Rev E 101(1):010203

    Article  Google Scholar 

  • Rudy Samuel H, Brunton Steven L, Proctor Joshua L, Nathan KJ (2017) Data-driven discovery of partial differential equations. Sci Adv 3(4):e1602614

    Article  Google Scholar 

  • Sargsyan K, Huan X, Najm HN (2019) Embedded model error representation for Bayesian model calibration. Int J Uncertain Quantif 9(4)

  • Schaeffer H (2017) Learning partial differential equations via data discovery and sparse optimization. Proc R Soc A Math Phys Eng Sci 473(2197):20160446

    MathSciNet  MATH  Google Scholar 

  • Schaeffer H, McCalla SG (2017) Sparse model selection via integral terms. Phys Rev E 96(2):023302

    Article  MathSciNet  Google Scholar 

  • Sgura I, Lawless AS, Bozzini B (2019) Parameter estimation for a morphochemical reaction-diffusion model of electrochemical pattern formation. Inverse Probl Sci Eng 27(5):618–647

    Article  MathSciNet  MATH  Google Scholar 

  • Trefethen LN (2000) Spectral methods in MATLAB, vol 10. SIAM, Philadelphia

  • Voss Henning U, Jens T, Jürgen K (2004) Nonlinear dynamical system identification from uncertain and indirect measurements. Int J Bifurcat Chaos 14(06):1905–1933

    Article  MathSciNet  MATH  Google Scholar 

  • Wang Z, Huan X, Garikipati K (2019) Variational system identification of the partial differential equations governing the physics of pattern-formation: Inference under varying fidelity and noise. Comput Methods Appl Mech Eng 356:44–74

    Article  MathSciNet  MATH  Google Scholar 

  • Xu H, Chang H, Zhang D (2019) Dl-pde: deep-learning based data-driven discovery of partial differential equations from discrete and noisy data. arXiv preprint arXiv:1908.04463

  • Yoshinaga N, Tokuda S (2020) Bayesian modelling of pattern formation from one snapshot of pattern. arXiv preprint arXiv:2006.06125

  • Zhao H, Storey BD, Braatz RD, Bazant MZ (2020) Learning the physics of pattern formation from images. Phys Rev Lett 124(6):060201

    Article  Google Scholar 

  • Zhao H, Braatz RD, Bazant MZ (2021) Image inversion and uncertainty quantification forconstitutive laws of pattern formation. J Comput Phys 436:110279

Download references

Acknowledgements

The author was supported through NSF award DMS-1908968.

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Arizona, Tucson, AZ, 85721, USA

    Karl Glasner

Authors
  1. Karl Glasner
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Karl Glasner.

Additional information

Communicated by Vinicius Albani.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Glasner, K. Data-driven learning of differential equations: combining data and model uncertainty. Comp. Appl. Math. 42, 36 (2023). https://doi.org/10.1007/s40314-022-02180-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-022-02180-y

Keywords

Mathematics Subject Classification

Search

Navigation