Control point reduction for lofted B-spline surface interpolation based on serial closed contours

Abstract

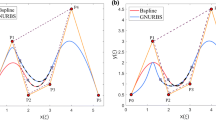
Modern shape design and capture techniques usually present geometric data in serial rows of data points, where the number of data points varies from row to row. Lofted or skinned B-spline surface interpolation is a technique that generates a B-spline surface that passes through these data points precisely. Traditional approach often causes a large increase in the number of control points of the resulting B-spline surface. However, much of the work to date in mitigating the effects of this increase (i.e., control point reduction) has been limited to open-section curves. The lofting of serial closed contours using interpolation techniques has not been addressed in the existing literature. The key is to find a condition, like the well-established Schoenberg–Whitney condition and its generalization in open B-spline curve interpolation, to establish the relationship between the domain knots and parameters, so that the system matrix is invertible or full-rank. This paper focuses on control point reduction in lofted B-spline surface interpolation from serial closed contours. The technical challenges of employing lofted B-spline surface interpolation to closed contours are comprehensively outlined and analyzed. We also derive a theorem that describes the relationship of numerical stability between the domain knots and parameters of the periodic B-splines. Then, we use the interpolation condition of the proposed theorem to extend the existing method of control point reduction to serial closed contours more naturally. Experimental results demonstrate that our algorithm produces a closed surface of the same quality as the open surfaces, but with significantly fewer control points.

A Proof of Lemma 1

Before providing the proof of Lemma 1, we introduce the following properties.

Fig. 13

The diagram of Property (1) by a cyclic knot vector with $p=3, n=6$

Property 1

Let $p=2k-1$ be the degree, ${\textbf {U}}_{\mathrm{{cyclic}}}^{n,p}(u_{i})$ be a cyclic knot vector, then the following statements hold:

• (1) $N_{(n+1)+i,p}(u+T) = N_{i,p}(u), \quad i = 0, \ldots , 2k-2$

• (2) $N_{i,p}(u-T) = N_{i+(n+1),p}(u), \quad i = 0, \ldots , 2k-2$

• (3) If $u \in [u_j,u_{j+1})$, then $N_{i,p}(u) \ge 0, \quad i = j, \ldots , j+p$

• (4) $u_a \le u_b$ if $a \le b$ (monotonicity of knot vector)

Proof

For parts (1) and (2), refer to Fig.  for an illustration. For part (3), refer to page 57 of Ref (Piegl and Tiller 1996a). $\square$

Property 2

Let $p=2k-1$ be the degree of periodic B-spline, $N^p[\mathbf{{u}}_i](u)$ and $N_{i, p}(u)$ be two B-spline basis functions, we have

• (1) $u_{n+1+j} = u_j + T, \quad j = 0, \ldots , k-1$

• (2) $u_{j} = u_{j+(n+1)} - T, \quad j = -k, \ldots , 0$

• (3) $N^p[\mathbf{{u}}_i](u) = N_{i+k-1, p}(u), \quad i=0, \ldots , n$

• (4) $N^p[\mathbf{{u}}_i](u) = 0 \text { if } u \notin I_i^k$ (local support property)

Proof

We prove part (1) by induction on j. Clearly, $u_{n+1} = u_0 + T$ holds for $j=0$. Assume now that the relation is true for some $j=\ell$, then by the induction hypothesis we obtain $u_{n+1+\ell } = u_\ell + T$. Next, for $j=\ell + 1$, applying $u_{j+1} = u_{j} + r_{j \bmod (n+1)}$ yields that

$$\begin{aligned} \begin{aligned} u_{(n+1)+\ell +1}&= u_{n+1+\ell } + r_{(n+1+\ell ) \bmod (n+1)} \\ {}&= u_\ell + T + r_\ell = u_\ell + T + (u_{\ell +1}-u_\ell ) \\ {}&= u_{\ell +1} + T \end{aligned} \end{aligned}$$

it follows that the identity holds for $j=\ell + 1$. Furthermore, part (2) can be proven similarly.

For part (3), since $N^p[\mathbf{{u}}_i](u)$ and $N_{i, p}(u)$ are associated with knot vectors $[u_{i-k}, \ldots , u_{i+k}]$, $[u_{i-2k+1}, \ldots , u_{i+1}]$, respectively. By definition in Eqs. (3) and (12), we know that ${\hat{\textbf{U}}}_{T}$ is a subset of $\mathbf{{U}}_{\mathrm{{cyclic}}}^{n,p}(u_i)$. Thus, $N^p[\mathbf{{u}}_i](u) = N_{i+k-1, p}(u)$, i.e., the property follows. $\square$

Property 3

Let $p=2k-1$ be the degree of periodic B-spline, and assume that $u \in [u_j, u_{j+1})$, and $n \ge p$, then we have

• (1) If $i \in [0, n]$, then $\hat{N}[\mathbf{{u}}_i](u) = N^p[\mathbf{{u}}_i](u)$ when $i \in [j-k+1, j+k]$.

• (2) If $j \in [0,k-2]$, then $\hat{N}[\mathbf{{u}}_{i+(n+1)}](u) = N^p[\mathbf{{u}}_{i+(n+1)}](u+T)$ when $i \in [j-k+1, -1]$.

• (3) If $j \in [n-k+1, n]$, then $\hat{N}[\mathbf{{u}}_{i-(n+1)}](u) = N^p[\mathbf{{u}}_{i-(n+1)}](u-T)$ when $i \in [n+1, j+k]$.

Proof

We first prove part (1). Since $j-k+1 \le i \text { and } i \le j+k$, then we have $j+1 \le i+k \text { and } j \ge i-k$. Namely, $u_{j+1} \le u_{i+k} \text { and } u_j \ge u_{i-k}$. Hence, $u \in [u_j, u_{j+1}) \subseteq [u_{i-k}, u_{i+k}] = I_i^k$. Next, we prove $u_{i+k} - u_{i-k} \le T, \ i=0, \ldots , n$. We divide the interval [0, n] into three parts, i.e., $i \in [0, k) \cup [k, n+1-k) \cup [n+1-k, n]$, then the proof consists of three steps:

(i) For $0 \le i < k$,

$$\begin{aligned} \begin{aligned}&\because n \ge p=2k-1 \ \Rightarrow i+k \le (n+1)+i-k \ \Rightarrow u_{i+k} \le u_{(n+1)+i-k} \\&\because u_{i-k} + T = u_{(n+1)+i-k} \ \Rightarrow u_{i+k} \le u_{i-k} + T \ \Rightarrow u_{i+k} - u_{i-k} \le T \end{aligned} \end{aligned}$$

(ii) For $k \le i < n+1-k$,

$$\begin{aligned} \begin{aligned}&\because i< n+1-k \text { and } k \le i \ \Rightarrow i+k< n+1 \text { and } i-k \ge 0 \\&\Rightarrow u_{i+k}< u_{n+1} \text { and } -u_{i-k} \le -u_0 \ \Rightarrow u_{i+k} - u_{i-k} < u_{n+1} - u_0 = T \end{aligned} \end{aligned}$$

(iii) For $n+1-k \le i \le n$,

$$\begin{aligned} \begin{aligned}&\because n \ge p=2k-1 \ \Rightarrow i+k-(n+1) \le i-k \ \Rightarrow u_{i+k-(n+1)} \le u_{i-k} \\&\because u_{i+k} = u_{i+k-(n+1)} + T \ \Rightarrow u_{i+k} - T \le u_{i-k} \ \Rightarrow u_{i+k} - u_{i-k} \le T \end{aligned} \end{aligned}$$

As a consequence, $u_{i+k} - u_{i-k} \le T$ holds for all $i \in [0, n]$. Then, we have $u-T, \ u+T \notin I_i^k$ when $u \in I_i^k$. According to the definition of $\hat{N}[\mathbf{{u}}_i](u)$, we obtain

$$\begin{aligned} \hat{N}[\mathbf{{u}}_i](u) = N^p[\mathbf{{u}}_i](u) \end{aligned}$$

For part (2), since $u+T \in [u_j+T, u_{j+1}+T)$, by Property (2.1) we have $u+T \in [u_{n+j+1}, u_{n+j+2})$ for $j \in [0, k-2]$. On the other hand, $i \in [j-k+1, -1]$, then we have

$$\begin{aligned} \begin{aligned}&\because i \ge j-k+1 \text { and } i \le -1 \le j-1 \\&\Rightarrow (n+1)+i+k \ge n+j+2 \text { and } n+i+2 \le n+j+1 \\&\Rightarrow u_{n+j+2} \le u_{n+1+i+k} \text { and } u_{n+j+1} \ge u_{n+2+i} > u_{n+1+i-k} \\&\Rightarrow u+T \in [u_{n+j+1}, u_{n+j+2}) \subseteq [u_{n+1+i-k}, u_{n+1+i+k}] = I_{i+(n+1)}^k \end{aligned} \end{aligned}$$

Next, we prove $u-T, \ u \notin I_{i+(n+1)}^k$ as follows.

$$\begin{aligned} \begin{aligned}&\because n \ge p=2k-1 \ \Rightarrow i+k-1 \le n+i-k \\&\because i \ge j-k+1 \ \Rightarrow j \le i+k-1 \le n+i-k \\&\Rightarrow j+1 \le n+i+1-k \Rightarrow u_{j+1} \le u_{n+i+1-k} \\&\Rightarrow u-T< u < u_{j+1} \le u_{n+i+1-k} \\&\Rightarrow u-T, \ u \notin I_{i+(n+1)}^k \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} \hat{N}[\mathbf{{u}}_{i+(n+1)}](u) = N^p[\mathbf{{u}}_{i+(n+1)}](u+T) \end{aligned}$$

For part (3), by Property (2.2) and $u-T \in [u_j-T, u_{j+1}-T)$, we obtain $u-T \in [u_{j-(n+1)}, u_{j-n})$ when $j \in [n-k+1, n]$.

$$\begin{aligned} \begin{aligned}&\because i \ge n+1 \ge j+1> j+1-k\text { and } i \le j+k \\&\Rightarrow i-(n+1)+k> j-n \text { and } i-(n+1)-k \le j-(n+1) \\&\Rightarrow u_{i-(n+1)+k} > u_{j-n} \text { and } u_{i-(n+1)-k} \le u_{j-(n+1)} \\&\Rightarrow u-T \in [u_{j-(n+1)}, u_{j-n}) \subseteq [u_{i-(n+1)-k}, u_{i-(n+1)+k}] = I_{i-(n+1)}^k \end{aligned} \end{aligned}$$

Again, $u, \ u+T \notin I_{i-(n+1)}^k$ can be derived as follows.

$$\begin{aligned} \begin{aligned}&\because i \le j+k \ \Rightarrow i-(n+1)-k \le j-(n-2k+1) \\&\because n \ge p=2k-1 \ \Rightarrow i-(n+1)-k \le j \ \Rightarrow u_{i-(n+1)-k} \le u_j \\&\Rightarrow u_{i-(n+1)-k} \le u_j \le u < u+T \\&\Rightarrow u, \ u+T \notin I_{i-(n+1)}^k \end{aligned} \end{aligned}$$

Thus,

$$\begin{aligned} \hat{N}[\mathbf{{u}}_{i-(n+1)}](u) = N^p[\mathbf{{u}}_{i-(n+1)}](u-T) \end{aligned}$$

To sum up, this completes our proof. $\square$

Proof of Lemma 1

First, we divide $j \in [0, n]$ into three cases ($k \ge 2$), i.e., $j \in [0, k-2] \cup [k-1, n-k] \cup [n-k+1, n]$.

(i) when $j \in [k-1, n-k]$, then $i=j-k+1, \ldots , j+k \subseteq [0, n]$, by Property (3.1) and Property (2.3), we have

$$\begin{aligned} \hat{N}[\mathbf{{u}}_{i \bmod (n+1)}](u) = \hat{N}[\mathbf{{u}}_{i}](u) = N^p[\mathbf{{u}}_i](u) = N_{i+k-1,p}(u) \end{aligned}$$

(ii) when $j \in [0, k-2]$, then $i \in [j+1-k, -1] \cup [0, j+k]$, for $i \in [0, j+k]$, the identity can be validated like part (i), so only $i \in [j+1-k, -1]$ needs to be considered.

$$\begin{aligned} \begin{aligned} \hat{N}[\mathbf{{u}}_{i \bmod (n+1)}](u)&= \hat{N}[\mathbf{{u}}_{i+n+1}](u) \\ {}&= N^p[\mathbf{{u}}_{i+n+1}](u+T) \ \ \qquad \qquad \longleftarrow \text {Property }(3.2) \\ {}&= N_{i+k-1+(n+1),p}(u+T) \quad \qquad \longleftarrow \text {Property } (2.3) \end{aligned} \end{aligned}$$

Because $i \in [j+1-k, -1]$, so $i+k-1 \in [j, k-2] \subseteq [0, k-2]$. By Property (1.1) we have

$$\begin{aligned} N_{i+k-1+(n+1),p}(u+T) = N_{i+k-1,p}(u) \end{aligned}$$

(iii) when $j \in [n-k+1, n]$, then $i \in [j-k+1, j+k] = [j+k-1, n] \cup [n+1, j+k]$, thus, we discuss the case for $i \in [n+1, j+k]$.

$$\begin{aligned} \begin{aligned} \hat{N}[\mathbf{{u}}_{i \bmod (n+1)}](u)&= \hat{N}[\mathbf{{u}}_{i-(n+1)}](u) \\ {}&= N^p[\mathbf{{u}}_{i-(n+1)}](u-T) \qquad \qquad \longleftarrow \text {Property }(3.3) \\ {}&= N_{i+k-1-(n+1),p}(u-T) \quad \qquad \longleftarrow \text {Property } (2.3) \end{aligned} \end{aligned}$$

Since $i \in [n+1, j+k]$, so $i+k-1-(n+1) \in [k-1, j+2k-1-(n+1)] \subseteq [k-1, 2k-2]$. By Property (1.2) we obtain

$$\begin{aligned} N_{i+k-1-(n+1),p}(u-T) = N_{i+k-1,p}(u) \end{aligned}$$

On the other hand, $i+k-1 \in [j, j+p]$, by Property (1.3), we have $N_{i+k-1,p}(u) \ge 0$. According to the partition of unity, i.e., $\sum _{i=j}^{j+p}N_{i,p}(u)=1$ (page 57 of Ref Piegl and Tiller 1996a), we know that at most 2k of the $\hat{N}[\mathbf{{u}}_{i}](u)$ are nonzero. Thus, the lemma follows. $\square$