Skip to main content
SpringerLink
Log in

Shifted Chebyshev spectral Galerkin method to solve stochastic Itô–Volterra integral equations driven by fractional Brownian motion appearing in mathematical physics

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

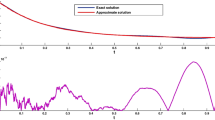
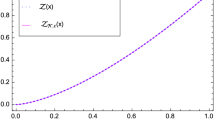
Abstract

The main aim of this article is to provide a spectral Galerkin method based on the shifted Chebyshev polynomial of the first kind to solve stochastic Itô–Volterra integral equations driven by fractional Brownian motion. The presented method uses the Gauss–Legendre quadrature rule and Itô approximation to reduce stochastic Itô–Volterra integral equations driven by fractional Brownian motion into the system of algebraic equations. Then Newton’s method is used to solve them numerically. Also, convergence and error analysis of the discussed scheme has been investigated in the Sobolev space. A few illustrative examples are discussed to show the applicability and reliability of the proposed method. Finally, the numerical results of the spectral Galerkin technique based on the shifted Chebyshev polynomial and shifted Chebyshev cardinal functions are compared to the actual solution.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Data availability statement

All data generated or analyzed during this study are included in this article.

References

  • Barikbin MS, Vahidi AR, Damercheli T, Babolian E (2020) An iterative shifted Chebyshev method for nonlinear stochastic Itô–Volterra integral equations. J Comput Appl Math 378:112912

    Article  MathSciNet  MATH  Google Scholar 

  • Biagini F, Hu Y, Øksendal B, Zhang T (2008) Stochastic calculus for fractional Brownian motion and applications. Springer Science and Business Media, New York

  • Canuto C, Hussaini MY, Quarteroni A, Zang TA (2007) Spectral methods: fundamentals in single domains. Springer Science and Business Media, New York

  • Hashemi SAS, Saeedi H (2021) ADM-TF hybrid method for nonlinear Itô–Volterra integral equations. Math Comput Simul 185:783–798

    Article  MATH  Google Scholar 

  • Hashemi B, Khodabin M, Maleknejad K (2017) Numerical solution based on hat functions for solving nonlinear stochastic Itô Volterra integral equations driven by fractional Brownian motion. Mediterr J Math 14(1):1–15

    Article  MATH  Google Scholar 

  • Heydari MH, Hooshmandasl MR, Shakiba A, Cattani C (2016) Legendre wavelets Galerkin method for solving nonlinear stochastic integral equations. Nonlinear Dyn 85(2):1185–1202

    Article  MathSciNet  MATH  Google Scholar 

  • Heydari MH, Mahmoudi MR, Shakiba A, Avazzadeh Z (2018) Chebyshev cardinal wavelets and their application in solving nonlinear stochastic differential equations with fractional Brownian motion. Commun Nonlinear Sci Numer Simul 64:98–121

    Article  MathSciNet  MATH  Google Scholar 

  • Heydari MH, Atangana A, Avazzadeh Z, Yang Y (2020) Numerical treatment of the strongly coupled nonlinear fractal-fractional Schrödinger equations through the shifted Chebyshev cardinal functions. Alex Eng J 59(4):2037–2052

    Article  Google Scholar 

  • Li X, Tang T, Xu C (2016) Numerical solutions for weakly singular Volterra integral equations using Chebyshev and Legendre pseudo-spectral Galerkin methods. J Sci Comput 67(1):43–64

    Article  MathSciNet  MATH  Google Scholar 

  • Longjin L, Ren FY, Qiu WY (2010) The application of fractional derivatives in stochastic models driven by fractional Brownian motion. Physica A Stat Mech Appl 389(21):4809–4818

    Article  MathSciNet  Google Scholar 

  • Maleknejad K, Mahmoudi Y (2004) Numerical solution of linear Fredholm integral equation by using hybrid Taylor and block-pulse functions. Appl Math Comput 149(3):799–806

    Article  MathSciNet  MATH  Google Scholar 

  • Maleknejad K, Sohrabi S, Rostami Y (2007) Numerical solution of nonlinear Volterra integral equations of the second kind by using Chebyshev polynomials. Appl Math Comput 188(1):123–128

    Article  MathSciNet  MATH  Google Scholar 

  • Mandelbrot BB, Van Ness JW (1968) Fractional Brownian motions, fractional noises and applications. SIAM Rev 10(4):422–437

    Article  MathSciNet  MATH  Google Scholar 

  • Mirzaee F, Solhi E, Naserifar S (2021) Approximate solution of stochastic Volterra integro-differential equations by using moving least squares scheme and spectral collocation method. Appl Math Comput 410:126447

    Article  MathSciNet  MATH  Google Scholar 

  • Mohammadi F (2016) Second kind Chebyshev wavelet Galerkin method for stochastic Itô–Volterra integral equations. Mediterr J Math 13(5):2613–2631

    Article  MathSciNet  MATH  Google Scholar 

  • Oksendal B (1998) Stochastic differential equations, an introduction with applications, 5th edn. Springer, New York

    MATH  Google Scholar 

  • Ray SS, Sahu PK (2018) Novel methods for solving linear and nonlinear integral equations. Chapman and Hall/CRC, Boca Raton

    Book  Google Scholar 

  • Saha Ray S, Singh S (2020) Numerical solution of nonlinear stochastic Itô–Volterra integral equation driven by fractional Brownian motion. Eng Comput 37(9):3243–3268

    Article  Google Scholar 

  • Saha Ray S, Singh S (2021) New stochastic operational matrix method for solving stochastic Itô–Volterra integral equations characterized by fractional Brownian motion. Stoch Anal Appl 39(2):224–234

    Article  MathSciNet  MATH  Google Scholar 

  • Singh P, Saha Ray S (2022) Two reliable methods for numerical solution of nonlinear stochastic Itô–Volterra integral equation. Stoch Anal Appl 40(5):891–913

    Article  MathSciNet  MATH  Google Scholar 

  • Soheili AR, Soleymani F (2016) A new solution method for stochastic differential equations via collocation approach. Int J Comput Math 93(12):2079–2091

    Article  MathSciNet  MATH  Google Scholar 

  • Wen X, Huang J (2021) A Haar wavelet method for linear and nonlinear stochastic Itô–Volterra integral equation driven by a fractional Brownian motion. Stoch Anal Appl 39(5):926–943

    Article  MathSciNet  MATH  Google Scholar 

  • Yousefi S, Razzaghi M (2005) Legendre wavelets method for the nonlinear Volterra–Fredholm integral equations. Math Comput Simul 70(1):1–8

    Article  MathSciNet  MATH  Google Scholar 

  • Youssri YH, Hafez RM (2020) Chebyshev collocation treatment of Volterra–Fredholm integral equation with error analysis. Arab J Math 9(2):471–480

    Article  MathSciNet  MATH  Google Scholar 

  • Zeng C, Yang Q, Chen YQ (2012) Solving nonlinear stochastic differential equations with fractional Brownian motion using reducibility approach. Nonlinear Dyn 67:2719–2726

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, National Institute of Technology, Rourkela, 769008, India

    P. K. Singh & S. Saha Ray

Authors
  1. P. K. Singh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. Saha Ray
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Saha Ray.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Communicated by Vasily E. Tarasov.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Singh, P.K., Saha Ray, S. Shifted Chebyshev spectral Galerkin method to solve stochastic Itô–Volterra integral equations driven by fractional Brownian motion appearing in mathematical physics. Comp. Appl. Math. 42, 120 (2023). https://doi.org/10.1007/s40314-023-02263-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-023-02263-4

Keywords

Mathematics Subject Classification

Search

Navigation