Skip to main content
SpringerLink
Log in

Some Einstein interaction geometric aggregation operators based on improved operational laws of complex q-rung orthopair fuzzy set and their applications

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

Abstract

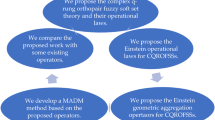
Complex q-rung orthopair fuzzy (CQROF) set is very feasible to depict the complex uncertain information in real-life problems because it is the modified concept from the complex Pythagorean and complex intuitionistic fuzzy sets. In this manuscript, we concentrate to analyze the improved Einstein operational laws for CQROF information. Then, based on the improved Einstein operational laws, we develop the complex q-rung orthopair fuzzy Einstein interaction weighted geometric (CQROFEIWG) operator, complex q-rung orthopair fuzzy Einstein interaction ordered weighted geometric (CQROFEIOWG) operator, and complex q-rung orthopair fuzzy Einstein interaction hybrid geometric (CQROFEIHG) operator. Furthermore, we analyze their major results and main three properties such as idempotency, boundedness, and monotonicity. Additionally, a decision-making approach with complex q-rung orthopair fuzzy information is developed, in which weights are handled objectively. Finally, some illustrated examples are used to demonstrate the supremacy and feasibility of the proposed approaches by comparing them with some existing ones.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Abbreviations

CQROF:

Complex q-rung orthopair fuzzy

CQROFEIWG:

Complex q-rung orthopair fuzzy Einstein interaction weighted geometric

CQROFEIOWG:

Complex q-rung orthopair fuzzy Einstein interaction ordered weighted geometric

CQROFEIHG:

Complex q-rung orthopair fuzzy Einstein interaction hybrid geometric

MADM:

Multi-attribute decision-making

FS:

Fuzzy sets

IFS:

Intuitionistic fuzzy set

PFS:

Pythagorean fuzzy set

QROFS:

Q-rung orthopair fuzzy set

CFS:

Complex fuzzy set

CIFS:

Complex intuitionistic fuzzy set

CPFS:

Complex Pythagorean fuzzy set

CQROFS:

Complex q-rung orthopair fuzzy set

References

  • Abbas M, Asghar MW, Guo Y (2022) Decision-making analysis of minimizing the death rate due to covid-19 by using q-rung orthopair fuzzy soft bonferroni mean operator. J Fuzzy Ext Appl 3(3):231–248

    Google Scholar 

  • Abdullah S, Al-Shomrani MM, Liu P, Ahmad S (2022) A new approach to three-way decisions making based on fractional fuzzy decision-theoretical rough set. Int J Intell Syst 37(3):2428–2457

    Google Scholar 

  • Abid MN, Yang MS, Karamti H, Ullah K, Pamucar D (2022) Similarity measures based on T-Spherical fuzzy information with applications to pattern recognition and decision making. Symmetry 14(2):410

    Google Scholar 

  • Akram M, Khan A (2021) Complex Pythagorean Dombi fuzzy graphs for decision making. Granul Comput 6:645–669

    MathSciNet  Google Scholar 

  • Akram M, Naz S (2019) A novel decision-making approach under complex Pythagorean fuzzy environment. Math Comput Appl 24(3):73

    MathSciNet  Google Scholar 

  • Akram M, Sattar A (2020) Competition graphs under complex Pythagorean fuzzy information. J Appl Math Comput 63(1):543–583

    MathSciNet  MATH  Google Scholar 

  • Akram M, Adeel A, Alcantud JCR (2018) Fuzzy N-soft sets: a novel model with applications. J Intell Fuzzy Syst 35(4):4757–4771

    Google Scholar 

  • Akram M, Adeel A, Alcantud JCR (2019) Hesitant fuzzy N-soft sets: a new model with applications in decision-making. J Intell Fuzzy Syst 36(6):6113–6127

    Google Scholar 

  • Akram M, Khan A, Borumand Saeid A (2020) Complex Pythagorean Dombi fuzzy operators using aggregation operators and their decision-making. Expert Syst 38(2):e12626

    Google Scholar 

  • Akram M, Kahraman C, Zahid K (2021a) Extension of TOPSIS model to the decision-making under complex spherical fuzzy information. Soft Comput 25(16):10771–10795

    Google Scholar 

  • Akram M, Khan A, Alcantud JCR, Santos-García G (2021b) A hybrid decision-making framework under complex spherical fuzzy prioritized weighted aggregation operators. Expert Syst 38(6):e12712

    Google Scholar 

  • Akram M, Al-Kenani AN, Shabir M (2021c) Enhancing ELECTRE I method with complex spherical fuzzy information. Int J Comput Intell Syst 14(1):1–31

    Google Scholar 

  • Akram M, Naz S, Edalatpanah SA, Mehreen R (2021d) Group decision-making framework under linguistic q-rung orthopair fuzzy Einstein models. Soft Comput 25(15):10309–10334

    MATH  Google Scholar 

  • Akram M, Bashir A, Edalatpanah SA (2021e) A hybrid decision-making analysis under complex q-rung picture fuzzy Einstein averaging operators. Comput Appl Math 40(8):1–35

    MathSciNet  MATH  Google Scholar 

  • Ali MI (2018) Another view on q-rung orthopair fuzzy sets. Int J Intell Syst 33(11):2139–2153

    Google Scholar 

  • Ali Z, Mahmood T (2020) Maclaurin symmetric mean operators and their applications in the environment of complex q-rung orthopair fuzzy sets. Comput Appl Math 39(3):1–27

    MathSciNet  MATH  Google Scholar 

  • Ali Z, Mahmood T (2022) Some Dombi aggregation operators based on complex q-rung orthopair fuzzy sets and their application to multi-attribute decision making. Comput Appl Math 41(1):1–40

    MathSciNet  MATH  Google Scholar 

  • Ali Z, Mahmood T, Yang MS (2020) TOPSIS method based on complex spherical fuzzy sets with Bonferroni mean operators. Mathematics 8(10):1739

    Google Scholar 

  • Ali Z, Mahmood T, Ullah K, Khan Q (2021) Einstein geometric aggregation operators using a novel complex interval-valued pythagorean fuzzy setting with application in green supplier chain management. Rep Mech Eng 2(1):105–134

    Google Scholar 

  • Alkouri AMDJS, Salleh AR (2012) Complex intuitionistic fuzzy sets. In: AIP conference proceedings (Vol. 1482, No. 1). American Institute of Physics. p 464–470

  • Ashraf S, Abdullah S, Aslam M, Qiyas M, Kutbi MA (2019) Spherical fuzzy sets and its representation of spherical fuzzy t-norms and t-conorms. J Intell Fuzzy Syst 36(6):6089–6102

    Google Scholar 

  • Atanassov K (1983) Intuitionistic fuzzy sets. In VII ITKR’s Session; Deposed in Central Sci.—Techn. Library of Bulg. Acad. of Sci., 1697/84; Sofia, Bulgaria, June 1983. (In Bulgarian)

  • Atanassov K (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20(1):87–96

    MathSciNet  MATH  Google Scholar 

  • Cai X, Han L (2014) Some induced Einstein aggregation operators based on the data mining with interval-valued intuitionistic fuzzy information and their application to multiple attribute decision making. J Intell Fuzzy Syst 27(1):331–338

    MathSciNet  MATH  Google Scholar 

  • Chen TY (2020) New Chebyshev distance measures for Pythagorean fuzzy sets with applications to multiple criteria decision analysis using an extended ELECTRE approach. Expert Syst Appl 147:113164

    Google Scholar 

  • Chen Z, Aghakhani S, Man J, Dick S (2010) ANCFIS: A neurofuzzy architecture employing complex fuzzy sets. IEEE Trans Fuzzy Syst 19(2):305–322

    Google Scholar 

  • Dick S (2005) Toward complex fuzzy logic. IEEE Trans Fuzzy Syst 13(3):405–414

    Google Scholar 

  • Farid HMA, Riaz M (2021) Some generalized q-rung orthopair fuzzy Einstein interactive geometric aggregation operators with improved operational laws. Int J Intell Syst 36(12):7239–7273

    Google Scholar 

  • Garg H (2016) Generalized intuitionistic fuzzy interactive geometric interaction operators using Einstein t-norm and t-conorm and their application to decision making. Comput Ind Eng 101:53–69

    Google Scholar 

  • Garg H, Rani D (2019a) Some results on information measures for complex intuitionistic fuzzy sets. Int J Intell Syst 34(10):2319–2363

    Google Scholar 

  • Garg H, Rani D (2019b) Complex interval-valued intuitionistic fuzzy sets and their aggregation operators. Fund Inform 164(1):61–101

    MathSciNet  MATH  Google Scholar 

  • Garg H, Rani D (2020a) Novel aggregation operators and ranking method for complex intuitionistic fuzzy sets and their applications to decision-making process. Artif Intell Rev 53:3595–3620

    Google Scholar 

  • Garg H, Rani D (2020b) Generalized geometric aggregation operators based on t-norm operations for complex intuitionistic fuzzy sets and their application to decision-making. Cogn Comput 12:679–698

    Google Scholar 

  • Gul M (2020) Application of Pythagorean fuzzy AHP and VIKOR methods in occupational health and safety risk assessment: the case of a gun and rifle barrel external surface oxidation and colouring unit. Int J Occup Saf Ergon 26(4):705–718

    Google Scholar 

  • Hajek P (1998) Metamathematics of fuzzy logic. Kluwer Academic Publishers, Dordrecht

    MATH  Google Scholar 

  • Hila K, Abdullah S (2014) A study on intuitionistic fuzzy sets in Γ-semihypergroups. J Intell Fuzzy Syst 26(4):1695–1710

    MathSciNet  MATH  Google Scholar 

  • Hussain A, Ullah K, Yang MS, Pamucar D (2022a) Aczel-Alsina aggregation operators on T-Spherical Fuzzy (TSF) information with application to TSF multi-attribute decision making. IEEE Access 10:26011–26023

    Google Scholar 

  • Hussain A, Ullah K, Alshahrani MN, Yang MS, Pamucar D (2022b) Novel Aczel-Alsina operators for Pythagorean fuzzy sets with application in multi-attribute decision making. Symmetry 14(5):940

    Google Scholar 

  • Jain R (1977) A procedure for multiple-aspect decision making using fuzzy sets. Int J Syst Sci 8(1):1–7

    MATH  Google Scholar 

  • Joshi BP, Singh A, Bhatt PK, Vaisla KS (2018) Interval valued q-rung orthopair fuzzy sets and their properties. J Intell Fuzzy Syst 35(5):5225–5230

    Google Scholar 

  • Khan M, Davvaz B, Yaqoob N, Gulistan M, Khalaf MM (2015) On (∈,∈ Vq k)-intuitionistic (fuzzy ideals, fuzzy soft ideals) of subtraction algebras. Songklanakarin J Sci Technol 37(4):465–475

    Google Scholar 

  • Khan MJ, Kumam P, Deebani W, Kumam W, Shah Z (2020) Distance and similarity measures for spherical fuzzy sets and their applications in selecting mega projects. Mathematics 8(4):519

    Google Scholar 

  • Khan MJ, Kumam P, Shutaywi M (2021a) Knowledge measure for the q-rung orthopair fuzzy sets. Int J Intell Syst 36(2):628–655

    Google Scholar 

  • Khan MJ, Alcantud JCR, Kumam P, Kumam W, Al-Kenani AN (2021b) An axiomatically supported divergence measures for q-rung orthopair fuzzy sets. Int J Intell Syst 36(10):6133–6155

    Google Scholar 

  • Khan R, Ullah K, Pamucar D, Bari M (2022) Performance measure using a multi-attribute decision making approach based on complex T-spherical fuzzy power aggregation operators. J Comput Cogn Eng 1(3):138–146

    Google Scholar 

  • Kumar T, Baja RK (2014) On complex intuitionistic fuzzy soft sets with distance measures and entropies. J Math 2014:972198

    MathSciNet  MATH  Google Scholar 

  • Liu P, Mahmood T, Ali Z (2019) Complex q-rung orthopair fuzzy aggregation operators and their applications in multi-attribute group decision making. Information 11(1):5

    Google Scholar 

  • Liu P, Ali Z, Mahmood T (2020) The distance measures and cross-entropy based on complex fuzzy sets and their application in decision making. J Intell Fuzzy Syst 39(3):3351–3374

    Google Scholar 

  • Liu P, Ali Z, Mahmood T (2021) Generalized complex q-rung orthopair fuzzy Einstein averaging aggregation operators and their application in multi-attribute decision making. Complex Intell Syst 7(1):511–538

    Google Scholar 

  • Ma X, Akram M, Zahid K, Alcantud JCR (2021) Group decision-making framework using complex Pythagorean fuzzy information. Neural Comput Appl 33:2085–2105

    Google Scholar 

  • Mahmood T (2020) A novel approach towards bipolar soft sets and their applications. J Math. https://doi.org/10.1155/2020/4690808

    Article  MathSciNet  MATH  Google Scholar 

  • Mahmood T, Ali Z (2021) Entropy measure and TOPSIS method based on correlation coefficient using complex q-rung orthopair fuzzy information and its application to multi-attribute decision making. Soft Comput 25(2):1249–1275

    MATH  Google Scholar 

  • Mahmood T, Ullah K, Khan Q, Jan N (2019) An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput Appl 31(11):7041–7053

    Google Scholar 

  • Mahmood T, Ali Z, Ullah K, Khan Q, AlSalman H, Gumaei A, Rahman SMM (2022) Complex Pythagorean fuzzy aggregation operators based on confidence levels and their applications. Math Biosci Eng 19(1):1078–1107

    MATH  Google Scholar 

  • Naeem K, Riaz M, Afzal D (2019) Pythagorean m-polar fuzzy sets and TOPSIS method for the selection of advertisement mode. J Intell Fuzzy Syst 37(6):8441–8458

    Google Scholar 

  • Ngan RT, Ali M, Tamir DE, Rishe ND, Kandel A (2020) Representing complex intuitionistic fuzzy set by quaternion numbers and applications to decision making. Appl Soft Comput 87:105961

    Google Scholar 

  • Ohlan R, Ohlan A (2022) A bibliometric overview and visualization of fuzzy sets and systems between 2000 and 2018. Ser Libr 81(2):190–212

    MATH  Google Scholar 

  • Rahman K, Sanam A, Saleem A, Muhammad YK (2020) Some induced generalized Einstein aggregating operators and their application to group decision-making problem using intuitionistic fuzzy numbers. Ann Optim Theory Pract 3(3):15–49

    Google Scholar 

  • Ramot D, Milo R, Friedman M, Kandel A (2002) Complex fuzzy sets. IEEE Trans Fuzzy Syst 10(2):171–186

    Google Scholar 

  • Ramot D, Friedman M, Langholz G, Kandel A (2003) Complex fuzzy logic. IEEE Trans Fuzzy Syst 11(4):450–461

    Google Scholar 

  • Rani D, Garg H (2017) Distance measures between the complex intuitionistic fuzzy sets and their applications to the decision-making process. Int J Uncertain Quantif 7(5):423–439

    MathSciNet  MATH  Google Scholar 

  • Riaz M, Hashmi MR (2019) Linear Diophantine fuzzy set and its applications towards multi-attribute decision-making problems. J Intell Fuzzy Syst 37(4):5417–5439

    Google Scholar 

  • Riaz M, Naeem K, Afzal D (2020a) Pythagorean m-polar fuzzy soft sets with TOPSIS method for MCGDM. Punjab Univ J Math 52(3):21–46

    MathSciNet  Google Scholar 

  • Riaz M, Hashmi MR, Kalsoom H, Pamucar D, Chu YM (2020b) Linear Diophantine fuzzy soft rough sets for the selection of sustainable material handling equipment. Symmetry 12(8):1215

    Google Scholar 

  • Riaz M, Pamucar D, Athar Farid HM, Hashmi MR (2020c) q-Rung orthopair fuzzy prioritized aggregation operators and their application towards green supplier chain management. Symmetry 12(6):976

    Google Scholar 

  • Sirbiladze G (2021a) New view of fuzzy aggregations. Part I: general information structure for decision-making models. J Fuzzy Ext Appl 2(2):130–143

    Google Scholar 

  • Sirbiladze G (2021b) New view of fuzzy aggregations. Part III: extensions of the FPOWA operator in the problem of political management. J Fuzzy Ext Appl 2(4):321–333

    Google Scholar 

  • Ullah K, Mahmood T, Ali Z, Jan N (2020) On some distance measures of complex Pythagorean fuzzy sets and their applications in pattern recognition. Complex Intell Syst 6(1):15–27

    Google Scholar 

  • Wang W, Liu X (2011) Intuitionistic fuzzy geometric aggregation operators based on Einstein operations. Int J Intell Syst 26(11):1049–1075

    Google Scholar 

  • Wang W, Liu X (2012) Intuitionistic fuzzy information aggregation using Einstein operations. IEEE Trans Fuzzy Syst 20(5):923–938

    Google Scholar 

  • Waqar M, Ullah K, Pamucar D, Jovanov G, Vranješ Ð (2022) An approach for the analysis of energy resource selection based on attributes by using Dombi T-Norm based aggregation operators. Energies 15(11):3939

    Google Scholar 

  • Yager RR (2013) June. Pythagorean fuzzy subsets. In 2013 joint IFSA world congress and NAFIPS annual meeting (IFSA/NAFIPS). IEEE, p 57–61

  • Yager RR (2016) Generalized orthopair fuzzy sets. IEEE Trans Fuzzy Syst 25(5):1222–1230

    Google Scholar 

  • Zadeh LA (1965) Fuzzy sets. Inf Control 8(3):338–353

    MATH  Google Scholar 

  • Zhan J, Khan M, Gulistan M, Ali A (2017) Applications of neutrosophic cubic sets in multi-criteria decision-making. Int J Uncertain Quantif 7(5):377–394

    Google Scholar 

  • Zhao X, Wei G (2013) Some intuitionistic fuzzy Einstein hybrid aggregation operators and their application to multiple attribute decision making. Knowl-Based Syst 37:472–479

    Google Scholar 

  • Zulqarnain RM, Xin XL, Garg H, Khan WA (2021) Aggregation operators of pythagorean fuzzy soft sets with their application for green supplier chain management. J Intell Fuzzy Syst 40(3):5545–5563

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Business Administration, Shandong Women’s University, Jinan, 250300, Shandong, China

    Peide Liu

  2. Department of Mathematics and Statistics, International Islamic University Islamabad, Islamabad, Pakistan

    Zeeshan Ali & Tahir Mahmood

Authors
  1. Peide Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zeeshan Ali
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Tahir Mahmood
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Peide Liu.

Ethics declarations

Conflict of interest

We declare that we do have no commercial or associative interests that represent a conflict of interests in connection with this manuscript. There are no professional or other personal interests that can inappropriately influence our submitted work. No conflict of interest exists in the submission of this manuscript.

Research involving human participants and/or animals

This article does not contain any studies with human participants or animals performed by any of the authors.

Additional information

Communicated by Graçaliz Pereira Dimuro.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, P., Ali, Z. & Mahmood, T. Some Einstein interaction geometric aggregation operators based on improved operational laws of complex q-rung orthopair fuzzy set and their applications. Comp. Appl. Math. 42, 131 (2023). https://doi.org/10.1007/s40314-023-02269-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-023-02269-y

Keywords

Search

Navigation