Novel computational technique for the direct estimation of risk-neutral density using call price data quotes

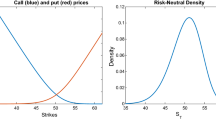
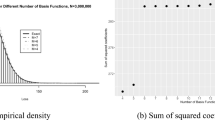
Abstract

This paper presents a new formulation for conveniently extracting the risk-neutral density (RND) function from the scarce data of the call price quotes, in the absence of any standard functional form. The existing solutions require primarily estimating the call price function under no-arbitrage conditions and then estimating the RND function. In this exposition, an independent relation is derived from the definition itself that connects RND to the call price function using tools like Laplace transform and Abel’s summation formula. This transforms the situation into a regression problem with simple constraints. The resulting linearly constrained least-square minimization problem gives an exact solution for the decision vector. The efficacy and accuracy of the proposed method are tested and validated on S &P 500 option price data.

A Preliminaries

Laplace transform. The Laplace transform of a function f(K), defined for all $K \ge 0$, is the function $F(\omega )$, which is a unilateral transform defined by

$$\begin{aligned} F(\omega ) = \int \limits _{0}^{\infty } f(K) e^{-\omega K} \,\textrm{d}K \end{aligned}$$

where $\omega$ is the transformation parameter. A necessary condition for existence of the integral is that f must be locally integrable on $[0,\infty )$. For locally integrable functions that decay at infinity or are of exponential order $|f(t)|\le A e^{B|t|}$, the integral can be understood as a proper Lebesgue integral. The notation is ${\mathcal {L}}_{K}[.](\omega )$ which is read as the Laplace transform of a function from variable K to variable $\omega$.

Final value theorem. In the theory of Laplace transform, the final value theorem (FVT) states that if both f(t) and $f'(t)$ have Laplace transforms that exist, then

$$\begin{aligned} \lim \limits _{K\rightarrow \infty } f(K) = \lim \limits _{\omega \rightarrow 0} \omega F(\omega ) , \end{aligned}$$

where $F(\omega )$ is the Laplace transform of f(K).

Abel summation formula. Let $A(t) = \sum _{0\le n\le t} a_{n}$ be the partial sum of a real-valued sequence $(a_{n})_{n=0}^{\infty }$, then for a continuously differentiable function $\phi (t)$ on $[0,\infty ]$, we have

$$\begin{aligned} \sum \limits _{n=0}^{\infty }a_{n} \phi (n) = \left( \lim _{x\rightarrow \infty } A(x)\phi (x) \right) - \int _{0}^{\infty } A(u)\phi '(u) \,\textrm{d}u. \end{aligned}$$

(25)

Abel’s summation formula, one gets an integral representation for a summation and vice versa. Using Abel’s summation formula can be generalized to the case where $\phi$ is only assumed to be continuous if the integral is interpreted as a Riemann–Stieltjes integral:

$$\begin{aligned} \sum \limits _{x<n\le y} a_{n} \phi (n) = A(y)\phi (y) - A(x)\phi (x) - \int \limits _{x}^{y}A(u)\,\textrm{d}\phi (u) . \end{aligned}$$

The discussion on the formula can be found in several sources, for instance, Chu (2007); Bǎnescu and Popa (2018).

Summation-by-parts. For $(f_k)_{0\le k\le n}$ and $(g_k)_{0\le k\le n}$, we have

$$\begin{aligned} \sum \limits _{k=0}^{n} f_k g_k = f_n \sum \limits _{k=0}^{n} g_k - \sum \limits _{j=0}^{n-1} (f_{j+1}-f_{j}) \sum \limits _{k=0}^{j} g_k \end{aligned}$$

for $n \in {\mathbb {N}}_0$.

First mean value theorem for integrals. Let $f: [a,b] \rightarrow {\mathbb {R}}$ be a continuous function, then there exists a constant $c \in (a,b)$ such that

$$\begin{aligned} \int \limits _{a}^{b}f(x)\,\textrm{d}x = (b-a)f(c) . \end{aligned}$$

The value f(c) can be essentially understood as the value of the function f(x) within a small interval [a, b].